Chapter 5 Discrete Probability Distributions

A random variable is

a function that assigns numerical values to the outcomes of an experiment

• Capturing uncertainty

• Summarizing outcomes of an experiment

• Using uppercase letter X to denote a random variable

• Using lowercase letter x to denote a numerical value that X may assume

two types of random variable

• Discrete random variable

• Continuous random variable

Discrete random variable:

Assuming a countable number of distinct values

Continuous random variable:

Assuming uncountable values within any interval

A discrete probability distribution is

a table, formula, or graph that describes the values of a discrete random variable and the probability associated with these values

Consider the experiment of rolling a die

• The probability distribution for rolling a die is:

• Each outcome has equally likely probability of 1/6

Graphically depict the probability distribution

The cumulative probability distribution provides

the probability that X is less than or equal to x: 𝑃(𝑋≤𝑥)

Consider the experiment of rolling a die

• The cumulative probability distribution for rolling a die is:

The probability of getting a four or less:

P(X ≤4) = 4/6 = 2/3

P(X=3) = P(X ≤3) – P(X ≤2) = 3/6 – 2/6 = 1/6

Two key properties of discrete probability distributions

• The probability of each value x is a value between 0 and 1

  • 0 ≤ P(X=𝑥)≤ 1

• The sum of the probabilities equals 1

  • ∑P(X=𝑥)=1

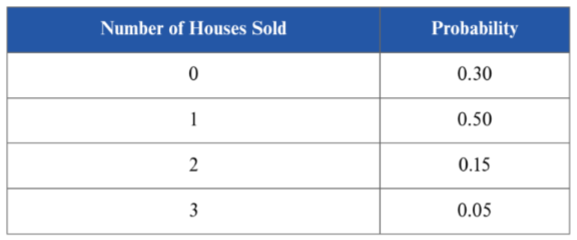
The number of homes that a realtor sells over a one-month period has the probability distribution shown in the table

• What is the probability that the realtor sells at most one house in a one-month period?

• What is the probability that the realtor sells at least two houses in a one-month period?

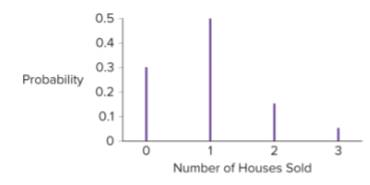
• Graphically depict the probability distribution and comment on its symmetry/skewness.

• What is the probability that the realtor sells at most one house in a one-month period?

  • P(X ≤ 1) = P(X = 0) + P(X = 1) = 0.3 + 0.5 = 0.8

• What is the probability that the realtor sells at least two houses in a one-month period?

  • P(X ≥ 2) = P(X = 2) + P(X = 3) = 0.15 + 0.05 = 0.2

• Graphically depict the probability distribution and comment on its symmetry/skewness.

  • The probability distribution shows not symmetric, but it is positively skewed

Three summary measures for a random variable

• Mean (Expected Value)

• Variance

• Standard Deviation

The expected value of the discrete random variable X is

a weighted average of all possible values of X

• Providing a measure of the central location of the distribution X

• Calculated as E(X)=μ=∑_(i=1)^n x_i∗P(X= x_i)

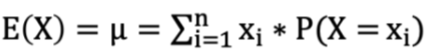
The measures of variance and standard deviation indicate

whether the values of X widely scattered from μ

• Providing measures of dispersion of the distribution X

• Calculated as Var (X)=𝜎^2=∑_(𝑖=1)^𝑛 (x_i−𝜇)^2 ∗P(X=x_i )

• Calculated as SD(X)=√(𝜎^2 )=σ=√(∑_(𝑖=1)^𝑛 (x_i−𝜇)^2 ∗P(X=x_i ) )

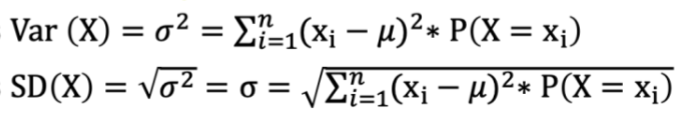
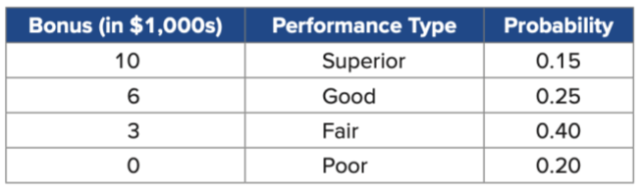
Brad Williams is the owner of a large car dealership in Chicago. Brad decides to construct an incentive compensation program that equitably and consistently compensates employees on the basis of their performance. (Using E(X)=∑_(i=1)^n x_i∗P(X= x_i))

1. Calculate the expected value of the annual bonus amount

2. Calculate the variance and standard deviation of the annual bonus amount (Using Var (X)=∑_(𝑖=1)^𝑛 (x_i−𝜇)^2 ∗P(X=x_i ) )

3. What is the total annual amount that Brad can expect to pay in bonuses if he has 25 employees

• Calculate the expected value of the annual bonus amount

  • 𝐸(𝑋)=𝜇=∑𝑥_𝑖∗𝑃(𝑋=𝑥_𝑖 ) =4.2 or $4,200

• Calculate the variance and standard deviation of the annual bonus amount (Using Var (X)=∑_(𝑖=1)^𝑛 (x_i−𝜇)^2 ∗P(X=x_i ) )

  • 𝑉𝑎𝑟(𝑋)=𝜎^2=∑(𝑥_𝑖−𝜇)^2 𝑃(𝑋=𝑥_𝑖 )=9.97 (in ($1,000s)^2)

  • 𝑆𝐷(𝑋)=𝜎=√(𝜎^2 )=√9.97=3.158 or $3,158

• What is the total annual amount that Brad can expect to pay in bonuses if he has 25 employees

  • If Brad has 25 employees, we can expect to pay

    $4,200*25 = $105,000 in bonuses

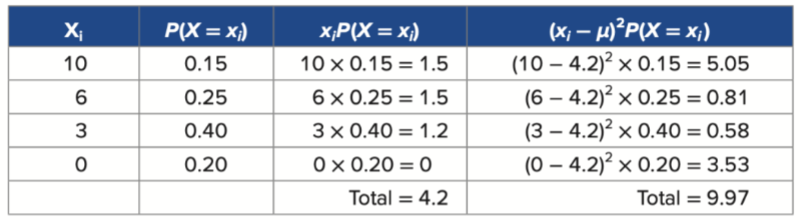
Suppose the table shows the probability distribution for the number of televisions in given household

• Calculate the expected value (Using E(X)=∑_(i=1)^n x_i∗P(X= x_i))

• Calculate the variance (Using Var (X)=∑_(𝑖=1)^𝑛 (x_i−𝜇)^2∗P(X=x_i ) )

• Calculate the standard deviation

• Calculate the expected value (Using E(X)=∑_(i=1)^n x_i∗P(X= x_i))

  • E(X)=𝜇=∑_(all x x∗P(X)=0∗P(0)+1∗P(1)+2∗P(2)+

    3∗P(3)+4∗P(4)+5∗P(5)=0∗0.012+1∗0.319+2∗0.374+3∗0.191+4∗0.076+

    5∗0.028=2.084

• Calculate the variance (Using Var (X)=∑_(𝑖=1)^𝑛 (x_i−𝜇)^2∗P(X=x_i ) )

  • Var(X)=𝜎^2=∑_(all x) (𝑥−𝜇)^2∗P(X)=(0−2.084)^2∗0.012+

    (1−2.084)^2∗0.319+(2−2.084)^2∗0.374+ (3−2.084)^2∗0.191+(4−2.084)^2∗0.076+(5−2.084)^2∗0.028=1.107

• Calculate the standard deviation

  • σ=√(𝜎^2 )=√1.107=1.052

Let X be

a random variable

Let c be

a constant

Laws of Expected Value

• E(c)=c

• E(X+c)=E(X)+c

• E(X∗c)=c∗E(X)

Laws of Variance

• Var(c)=0

• Var(X+c)=Var(X)

• Var(X∗c)=c^2∗Var(X)

Suppose the average score on the first test is 80, and the variance is 10. If a professor decided to add 5 points to each student’s grade.

• Calculate the new average score

• Calculate the new variance

• Calculate the new average score

  • E(X+c)=E(X)+c=80+5=85

• Calculate the new variance

  • Var(X+𝑐)=Var(X)=10

Suppose the average score on the first test is 80, and the variance is 10. If a professor decided to multiply by 1.1 to each student’s grade.

• Calculate the new average score

• Calculate the new variance

• Calculate the new average score

  • E(c∗𝑋)=𝑐∗𝐸(𝑋)=1.1∗80=88

• Calculate the new variance

  • Var(c∗X)=𝑐^2∗Var(X)=1.1^2∗10=12.1

Different types of experiments generate different probability distributions

• The Binomial Distribution

• The Poisson Distribution

• The Hypergeometric Distribution

A binomial random variable X is defined as

the number of successes achieved in the n trials of a Bernoulli process of an experiment

• A Bernoulli process consists of a series of n independent and identical trials of an experiment

  • (Only two possible outcomes: success (p) and failure (1 - p))

• The possible values (X) include 0, 1,…, n

Binomial Experiment

• Fixed number (n) of trials

• Two possible outcomes for each trial (“success” and “failure”)

• P(success) = p, P(failure) = 1 − p

• Trials are independent: outcome of one trial does not affect the outcomes of any other trials

Binomial Experiment Examples

• A customer defaults or does not default on a loan

• The number of heads in ten tosses of a fair coin

• A drug is either effective or ineffective

For a binomial random variable X, the probability of x successes in n Bernoulli trials is

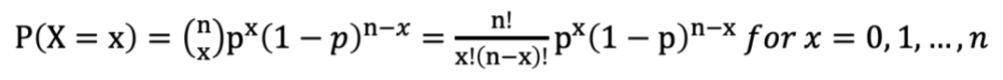
Example question: Find the probability of getting 2 times of head when flipping a coin 5 times (p = 0.5, x = 2, n = 5)

(5! / (2!(5-2)!)) (.5)² ((1-.5)^(5-2))= .3125

Factorial of a non-negative integer n, denoted by n!

• n!=n ×(𝑛−1)×(𝑛−2)×… ×2×1

• 5!=5×4×3×2×1=120

• 0!=1 (by definition)

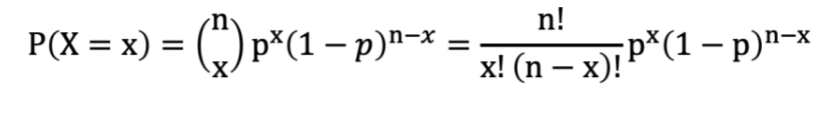
Pat is a student who is taking a test and his exam strategy is guessing the answers. There are 10 multiple choice questions with five possible answers in the exam. If there is only one answer for each question,

• What is the probability that Pat gets no answers correct?

• What is the probability that the Pat gets two answers correct?

• What is the probability that Pat gets no answers correct?

  • P(X=0)=10!/0!(10−0)! 0.2^0 (1−0.2)^(10−0)=1∗1∗(0.8)^10≈0.1074

• What is the probability that the Pat gets two answers correct?

  • P(X=2)=10!/2!(10−2)! 0.2^2 (1−0.2)^(10−2)=45∗0.04∗(0.8)^8≈0.302

For a binomial random variable X, the probability of x successes in n Bernoulli trials

• Expected Value

  • E(X)=μ=n∗p

• Variance

  • Var(X)=σ^2=npq=np∗(1−p)

• Standard Deviation

  • SD(X)=σ=√(np∗(1−P))

Pat is a student who is taking a test and his exam strategy is guessing the answers. There are 10 multiple choice questions with five possible answers in the exam. If there is only one answer for each question,

• Expected value:E(X)=μ=np

• Variance:Var(X)=σ^2=npq=np∗(1−p)

Calculate the expected mean, variance, and standard deviation.

n=10, p=0.2

• E(X)=μ=np=10∗0.2=2

• Var(X)=σ^2=np∗(1−p)=10∗0.2∗0.8=1.6

• SD(X)=σ=√(np∗(1−P))=√1.6=1.26

In the U.S., about 30% of adults have four-year college degrees (U.S. Census Bureau, 2018). Suppose five adults are randomly selected P(X=x)=n!/x!(n−x)! p^x (1−p)^(n−x),E(X)=np,Var(X)=npq=np∗(1−p)

• Find the probability that none of adults has a college degree?

• Find the probability that no more than two of the adults have a college degree?

• Find the probability at least two of adults have a college degree?

• Calculate the expected value, variance, and standard deviation

• Find the probability that none of adults has a college degree?

  • P(X=0)=5!/0!(5−0)! 0.3^0 (1−0.3)^(5−0)=1∗1∗(0.7)^5≈0.1681

• Find the probability that no more than two of the adults have a college degree?

  • P(X≤2)= P(X=0)+P(X=1)+P(X=2)

    P(X=1)=5!/1!(5−1)! 〖0.3〗^1 (1−0.3)^(5−1)=5∗0.3∗(0.7)^4≈0.3602

    P(X=2)=5!/2!(5−2)! 〖0.3〗^2 (1−0.3)^(5−2)=10∗0.09∗(0.7)^3≈0.3087

    P(X≤2)=0.1681+0.3602+0.3087=0.8307

• Find the probability at least two of adults have a college degree?

  • P(X≥2)=1−[P(X=0)+P(X=1)]=1−(0.1681+0.3602)

    = 0.4717

• Calculate the expected value, variance, and standard deviation

  • E(X)=μ=np=5∗0.3=1.5 adults

    Var(X)=σ^2=np∗(1−p)=5∗0.3∗0.7=1.05

    SD(X)=σ=√(np∗(1−P))=√1.05=1.02

Excel and R functionality

• Example question 1: Find the probability of getting 5 times of head when flipping a coin for 10 times

• Example question 2: Find the probability of getting 4 times of head or less when flipping a coin for 10 times

• (x = 5 , n = 10, p = 0.5) 𝑃(𝑋=5)=BINOM.DIST (5, 10, 0.5, 0)≈0.2461

• 𝑃(𝑋≤4)=BINOM.DIST (4, 10, 0.5, 1)≈0.377