Normal Applied Year 1 definitions

Population

Entire set of items in the group being studied

Census

Measuring every member of a population

• accurate

• Expensive

• Some testing destroys items

• Time consuming

• Hard to process large quantity of data

Sampling frame

List of sampling units. Sampling units individually named or numbered.

E.g. database of ___ who/which___

Sample

Subset of the population intended to represent the population.

• less time consuming and expensive

• Less data to process

• Not as accurate

• Sample may not be large enough to give info on smaller subgroups

Sampling units

Individual units of a population

ALWAYS MENTION SAMPLING FRAME FOR ANY SAMPLING TECHNIQUE!!!!

Simple random sampling (definition, pros, cons)

• every member if population has equal chance of being selected

• In sampling frame, each item has unique identifying number

• Use random number generator/lottery sampling

• Free of bias

• Easy and cheap

• Not suitable for large pop.

• Need sampling frame

Systematic sampling (definition, pros, cons)

• Required elements chosen at regular intervals from ordered list

• Pick first item randomly by picking random number between 1 and k

• K = pop. size/ sample size

• Quick to use

• Need sampling frame

• Suitable for large pop.

• Patterns in sample data may occur

Stratified sampling

• Population divided into mutually exclusive strata (groups) and random sample taken from each

• Proportion stays same

• No. Sampled in strata = (no. in stratum/no. in population) x overall sample size

• Accurately represents population structure

• Population must be classified in strata so need to know population structure which can be hard to tell clearly wnd time consuming

• Rest of cons same as random sampling

Why can different samples reach different conclusions

Natural variation in population

What to say when asked to comment on a claim

• whether its mean, median, mode (median better with outliers. Can also mean half good/half not etc)

• Whether data supports company claim

How to improve data sampling reliability

• take larger sample

• Use simple random sampling

Quota sampling

• population divided into strata according to characteristics. Size set to try and reflect group proportion of whole population.

• Strata filled by interviewer/researcher

• No sampling frame needed

• Non random so potential bias

• Quick, easy and small sample still representative

• Time consuming and expensive to divide into strata

Opportunity sampling

• Sampling taken from people available at the time of the study

• Easy to carry out

• Cheap

• Unlikely to be representative

• Highly dependent on individual researcher so bias

Qualitative

Non-numerical

Quantitative

Numerical. Discrete(specific values) or continuous(any value)

Key terms for intervals

• class intervals

• Lower/upper class boundaries

• Class width

• Midpoint

UK stations from south of UK to north and weather conditions

Are in alphabetical order (except heathrow and hurn which are not). Ones in south warmer and more sunlight

• cambourne - coastal so windy and rainier

• Hurn- coastal so windy and rainier.

• Heathrow- warmest

• Leeming- pretty warm but more in north

• Leuchars- coastal. Wettest, coldest, windiest, furthest north.

When did the great storm happen

• October 15-16, 1987 . High wind speeds. Mostly SE affected

When is large data set recorded for

May to october in 1987 and in 2015.

Only 6 months so bit of a disadvantage.

International stations and weather conditions

• Perth, Australia - when summer here, winter there. Very hot in summer. 0 to very high rainfall

• Beijing, China- very hot and rainy in summer, very cold in winter. Inland

• Jacksonville, Florida, USA - very hot and humid, prone to hurricanes. Hurricane in oct ‘87 and oct 2015.

Special fact about 2015 may

Windiest month

Special fact about may 1987

Lots of missing data

Rainfall ‘tr’ meaning

Trace. Treat as 0 in calculation

N/A meaning

Reading not available so cant use in sample

Cloud cover special fact

• Measured in oktas. Quantitative

• Discrete Values 0-8

Max. Gust special fact

• Measure in knots

• 1kn =1.15mph

• Integers only

Cardinal wind directions

Directions on a compass

Daily mean temp units

Degrees celcius

Daily total rainfall units

mm

Daily mean pressure units

hPa. 1hPa= 100Pa

Integers only

Windspeed units

Beaufort scale- fresh, light, moderate, strong.

Qualitative.

Wind/gust direction

Bearings.

Multiples of 10 only

Daily total sunshine units

Hours.

Relative humidity units

%.

Integers only

Daily mean visibility units

Dm. 1Dm=10m.

Round to nearest 100

As you move further north from may to october, what happens to maximum hours of sunshine

Increases

Also consider size of sample and geographical factors affecting things, not just numerical values!!!

Humidity for fog

>95%

Outliers meaning

Unusual data

Anomallies meaning

Errors

Mean (x bar)

sum of x/n or sum of fx/sum of f

For listed data, Upper quartile

3n/4

For listed data , Lower quartile

n/4

For listed data, Median

n/2

For listed data, what if values for upper quartile/median/lower quartile are decimals

Round up

For listed data, what if values for upper quartile/median/lower quartile are whole numbers

Find midpoint with next one

Quartiles for grouped data

• lower: n/4

• Upper: 3n/4

• Median: n/2

• DO NOT ROUND, USE LINEAR INTERPOLATION

Percentiles

E.g. 57th percentile, P57= 0.57 x n

Deciles

10% chunks

E.g. D3 =0.3 x n

True class limit for ‘10-12’

9.5 <= x < 12.5

Interquartile range (is a measure of spread)

Upper - lower quartile

Ignores extremes

Interpercentile range

E.g. 10th to 90th IPR = P90 - P10

Variance (sigma squared)

MSMSM (mean of the squares minus the square of the means)

(Sum of x²/n) - mean² = Sxx/n

Grouped frequency used midpoint of class width to find f(x)

Standard deviation (sigma)

Sqrt (variance)

For some questions, can make assumptions that data is equally distributed through range

Variance definition

Measure of spread that takes all values into account. Average squared distance from mean.

Standard deviation definition

Measure of spread of data. How many values on each side of mean/median

Coding - if y=ax+b

Data values coded to make new set of values easier to work with

• Mean of y = a x (mean of x) + b

• Standard deviation of y = a x (standard deviation of x)

Cumulative frequency graphs and box plots

Use highest number in range for class

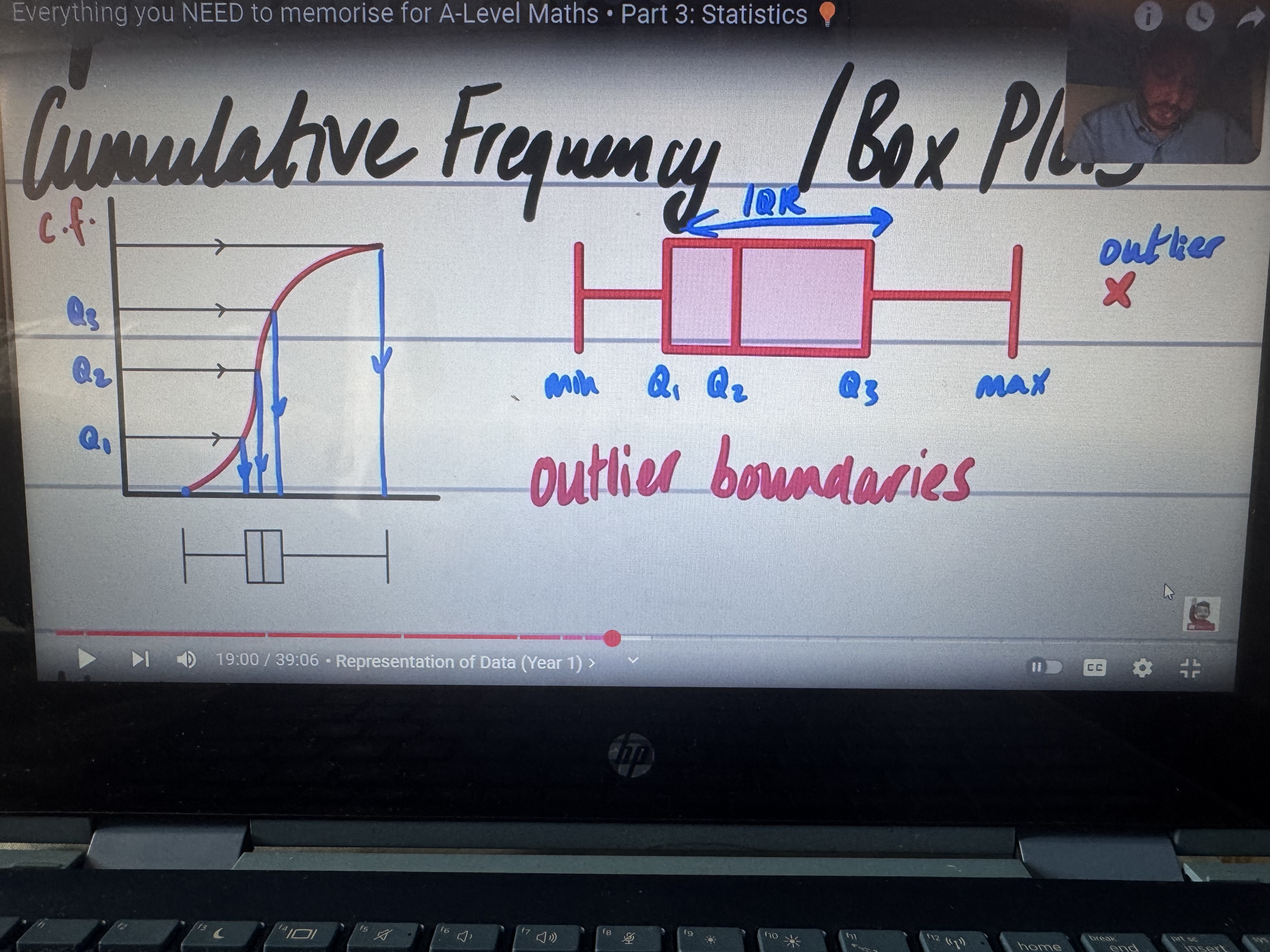
Standard way for finding outlier boundaries

• Must be less than this: (LowerQ) - 1.5 x IQR or

• Must be greater than this: (UpperQ) + 1.5 x IQR

What is meant by cleaning the data

Removing anomalies from data

Histograms

Joining middle of top of each bar forms frequency polygon

When comparing data sets on histograms/ box plots, comment on:

• mean and standard deviation OR

• median and interquartile rangE

If data set contains extreme values, median and IQR more appropriate

Correlation

Describes measure of linear relationship between 2 variables. Between -1 and 1

• strong negative

• Weak negative

• No/zero

• Weak positive

• Strong positive

Bivariate data

Data which has pairs of values for 2 variables. On scatter diagrams. E.g. pulse beats per minute

What variable goes on x-axis

Independent variable

Causal relationship

If one variable causes change in another. *just because 2 variables show correlation doesnt mean they have causal relationship. Must use context and common sense to deduce.

When can outliers be included in data for correlation, and when excluded

Included as they may unlikely be an anomally.

Exclude as they may not be representative.

Regression line

Line of best fit. y = mx + c.

c is y when x=0

m is rate of change of y with x. How much y increase/decreases with increase/decrease in x

Least squares regression line

Straight line that minimises sum of squares of distances of each data point from line

To improve regression line or any models…

Always increase sample size and choose randomly

Can you use regression line equation to find values of x when given y

No because x is independent variable

Interpolation

Estimating inside data range. Reliable.

Extrapolation

Estimating outside data range. Unreliable as we dont know graph continues to be linear.

What to do for non linear equations to draw linear graphs

Take logs

Venn diagrams

Represents events graphically

Rectangle represents sample space

Experiment

Repeatable process that gives rise to a number of outcomes

Event

Collection of 1 or more outcomes

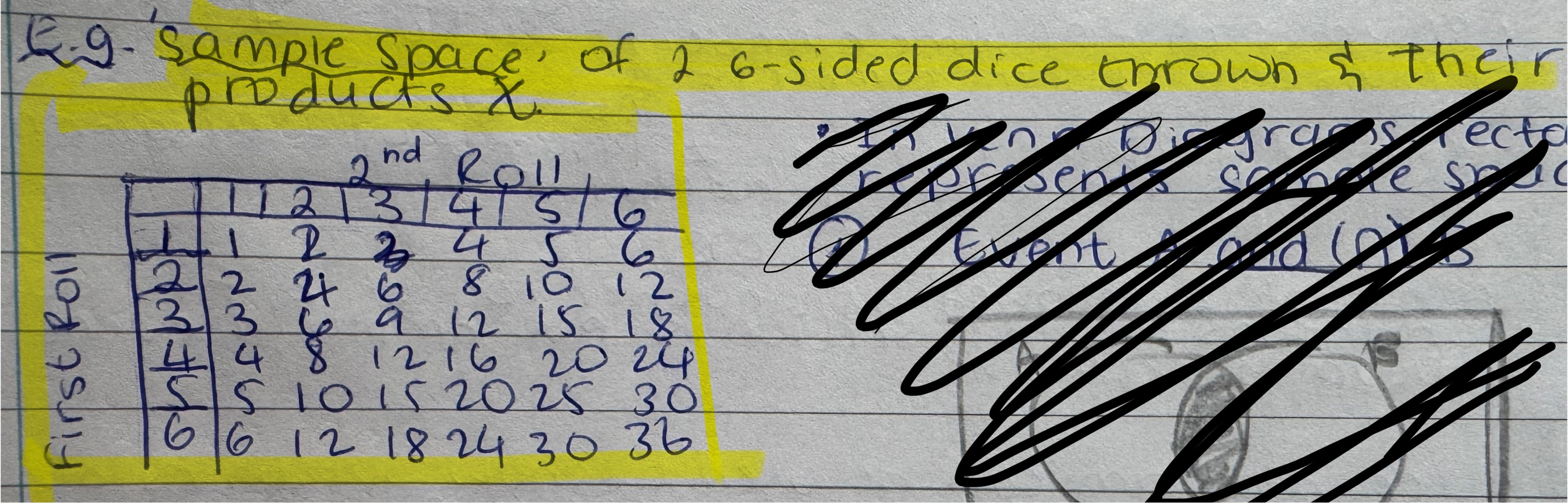
Sample space

Set of all possible outcomes. Could use table, tree diagram, or venn diagram

Mutually exclusive events

When events have no outcomes in common. Venn diagrams do not overlap.

P(A or B) = P(A) + P(B)

P (A and B) = 0

Independent events

When one event has no effect on another. Can’t tell from venn diagram so must do some calculations to determine if independent

P(A and B) = P(A) x P(B)

Probability addition law

P(A U B) = P(A) + P(B) - P(A and B).

*When events are mutually exclusive, P(A and B) must be 0 and if not 0, events are not mutually exclusive

Discrete uniform distribution

Probabilities of all outcomes are equal

Sum of probabilities of all outcomes of an event

1

Are the number of days in a given week discrete

No. Days in a week is always 7 and is pre-determined so not random.

When can you model X with binomial distribution X~B(n,p)

FFIT

• Fixed number of trials

• Fixed probability of success

• Independent trials

• Two outcomes only

Binomial X~B(n,p) equation for P(X=r)

(nCr)(p^r)(1-p)^(n-r)

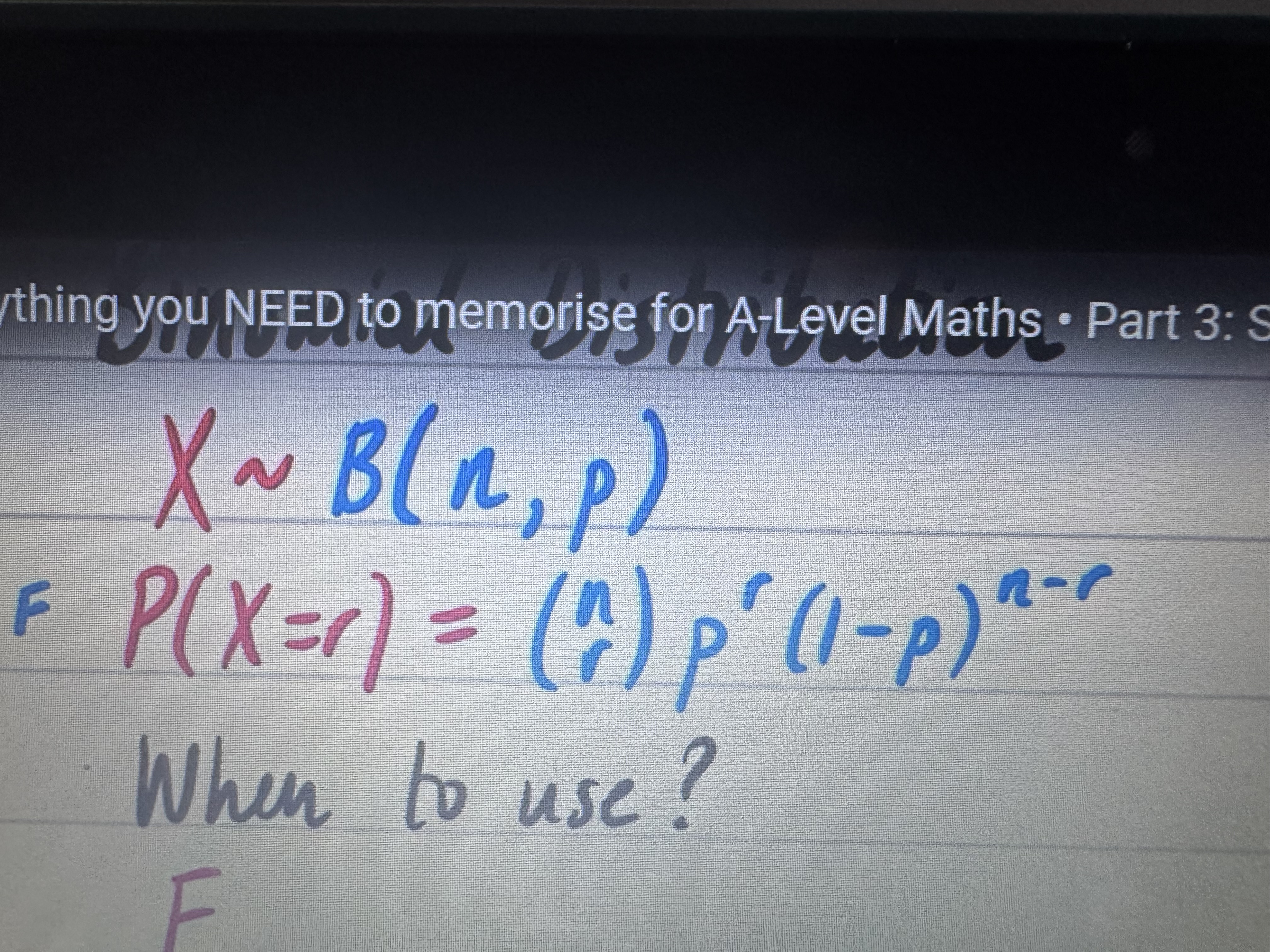
Hypothesis

A statement about a population parameter.

Test statistic

Result of the experiment or the statistic calculated. E.g. no. of people saying they support a candidate

Null hypothesis

Ho- what you assume to be true

Alternative hypothesis

What would be true if Ho is wrong

Significance level

The given threshold of likeliness

One tailed test

When H1: p>k or p<k

2 tailed test

When H1: p doesnt not equal k. Halve significance level value for each end

When to reject Ho

If p<sig. level (in critical region so sufficient evidence to reject Ho)

If p>sig. level, not in critical region so insufficient evidence to reject Ho

Critical region

If test statistic falls within this region, would cause you to reject null

Critical value

First value to fall inside critical region