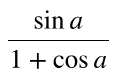Trig Identities

0.0(0)
studied byStudied by 1 person
learnLearn
examPractice Test
spaced repetitionSpaced Repetition
heart puzzleMatch
flashcardsFlashcards
Card Sorting

1/33

flashcard set

Earn XP

Description and Tags

Pre-Calculus

Trig

Trigonometry

University/Undergrad

Study Analytics
Name
Mastery
Learn
Test
Matching
Spaced

No study sessions yet.

34 Terms

1
New cards

Pythagorean Identity for Sine and Cosine

sin^2x + cos^2x = 1

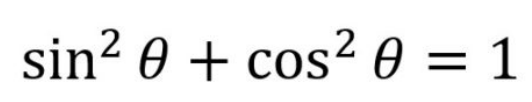
<p>sin^2x + cos^2x = 1</p>
2
New cards

Pythagorean Identity for Tangent and Secant

1 + tan^2x = sec^2x

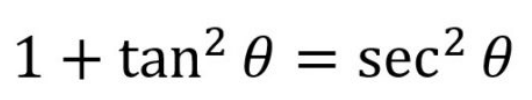
<p>1 + tan^2x = sec^2x</p>
3
New cards

Pythagorean Identity for Cotangent and Cosecant

1 + cot^2x = csc^2x

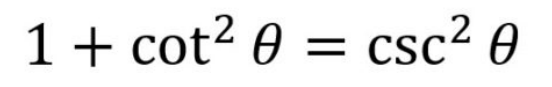
<p>1 + cot^2x = csc^2x</p>
4
New cards

Quotient Identity of Tangent

sinx/cosx

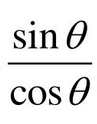
<p>sinx/cosx</p>
5
New cards

Quotient Identity of Cotangent

cosx/sinx

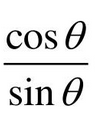
<p>cosx/sinx</p>
6
New cards

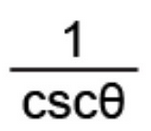
Reciprocal Identity of Sine

1/cscx

<p>1/cscx</p>
7
New cards

Reciprocal Identity of Cosecant

1/sinx

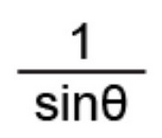
<p>1/sinx</p>
8
New cards

Reciprocal Identity of Cosine

1/secx

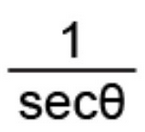
<p>1/secx</p>
9
New cards

Reciprocal Identity of Secant

1/cosx

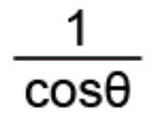
<p>1/cosx</p>
10
New cards

Reciprocal Identity of Tangent

1/cotx

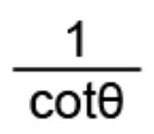
<p>1/cotx</p>
11
New cards

Reciprocal Identity of Cotangent

1/tanx

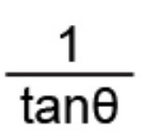
<p>1/tanx</p>
12
New cards

Sum of Two Angles Sine

sin(A+B) = sinAsinB + cosAcosB

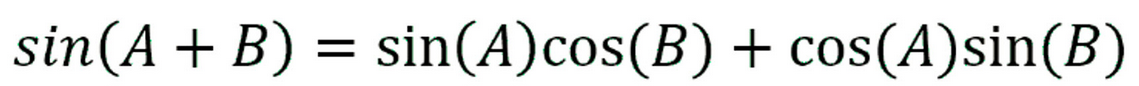
<p>sin(A+B) = sinAsinB + cosAcosB</p>
13
New cards

Difference of Two Angles Sine

sin(A-B) = sinAsinB - cosAcosB

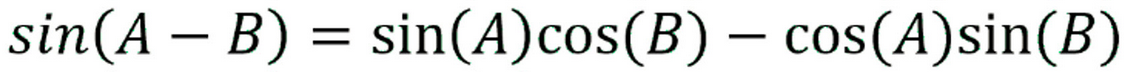
<p>sin(A-B) = sinAsinB - cosAcosB</p>
14
New cards

Sum of Two Angles Cosine

cos(A+B) = cosAcosB - sinAsinB

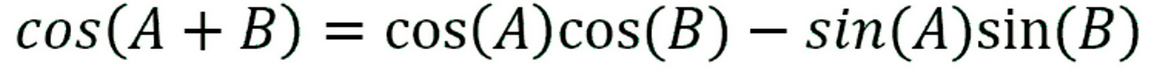
<p>cos(A+B) = cosAcosB - sinAsinB</p>
15
New cards

Difference of Two Angles Cosine

cos(A-B) = cosAcosB + sinAsinB

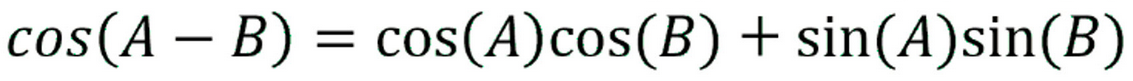
<p>cos(A-B) = cosAcosB + sinAsinB</p>
16
New cards

Sum of Two Angles Tangent

tan(A+B) = [tanA + tanB] / [ 1 - tanAtanB]

<p>tan(A+B) = [tanA + tanB] / [ 1 - tanAtanB]</p>
17
New cards

Difference of Two Angles Tangent

tan(A-B) = [tanA - tanB] / [ 1 + tanAtanB]

<p>tan(A-B) = [tanA - tanB] / [ 1 + tanAtanB]</p>
18
New cards

Double Angle: sin2x

2sinxcosx

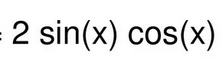
<p>2sinxcosx</p>
19
New cards

Double Angle: tan2x

[2tanx] / [ 1- tan^2 x ]

<p>[2tanx] / [ 1- tan^2 x ]</p>
20
New cards

Double Angle: cos2x

cos^2 x - sin^2 x

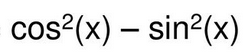
<p>cos^2 x - sin^2 x</p>
21
New cards

(Derivation) Double Angle: cos2x

1- 2sin^2 x

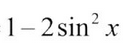
<p>1- 2sin^2 x</p>
22
New cards

Negative Angle Formula: sin (-x)

-sinx

23
New cards

Negative Angle Formula: cos (-x)

cosx

24
New cards

Negative Angle Formula: tan (-x)

-tanx

25
New cards

Negative Angle Formula: csc (-x)

-cscx

26
New cards

Negative Angle Formula: sec (-x)

secx

27
New cards

Negative Angle Formula: cot (-x)

-cotx

28
New cards

Power Reducing Identity: sin^2 x

sin^2 x = [1 - cos (2x)] / 2

<p>sin^2 x = [1 - cos (2x)] / 2</p>
29
New cards

Power Reducing Identity: cos^2 x

cos^2 x = [1 + cos (2x)] / 2

<p>cos^2 x = [1 + cos (2x)] / 2</p>
30
New cards

Power Reducing Identity: tan^2 x

[ 1 - cos (2x)] / [ 1 + cos (2x)]

<p>[ 1 - cos (2x)] / [ 1 + cos (2x)]</p>
31
New cards

Half Angle Formula for Sine

+/- square root of [ ( 1 - cosx ) / 2 ]

<p>+/- square root of [ ( 1 - cosx ) / 2 ]</p>
32
New cards

Half Angle Formula for Cosine

+/- square root of [ ( 1 + cosx ) / 2 ]

<p>+/- square root of [ ( 1 + cosx ) / 2 ]</p>
33
New cards

Half Angle Formula for Tangent

+/- square root of [( 1-cosx) / (1 + cosx)]

<p>+/- square root of [( 1-cosx) / (1 + cosx)]</p>
34
New cards

(Derivation) Half Angle Formula for Tangent

sinx / (1 + cos x)

<p>sinx / (1 + cos x)</p>