1.5 Inverse Functions and Logarithms

An inverse function "undoes" another function

What is an inverse function ?

If f is a function that takes an input x and gives an output y,

y=f(x)

then its inverse function f^−1 takes y as an input and returns x:

x=f−1(y)

A function has an inverse only if it is one-to-one

One to One Function

A function f is called a one-to-one function if it never takes on

the same value twice

Horizontal Line Test

A function is one-to-one if and only if no horizontal line

intersects its graph more than once.

What makes let’s a graph have an inverse function ? 

Let f be a one-to-one function with domain A and range B.

Then its inverse function f21 has domain B and range A. 

How to find the Inverse Function of a One to One Function f

STEP 1 Write y= f(x).

STEP 2 Solve this equation for x in terms of y (if possible).

STEP 3 To express f^-1 as a function of x, interchange x and y.

The resulting equation is y= f^-1(x)

What are logarithmic Functions with base b ?

Definition:

logb (x)= y if and only if by=x

Base constraints: The base

b must be positive ( b>0) and cannot equal 1 (b≠1)

Inverse relationship: Logarithmic functions are the inverse of exponential functions. If you have an exponential function like

f(x)=b^x its inverse is f^-1 (x)=log b (x)

Laws of Logarithms 

Natural Logarithms

The logarithm with base e is called the natural logarithm and has a special notation:

Natural Logarithm

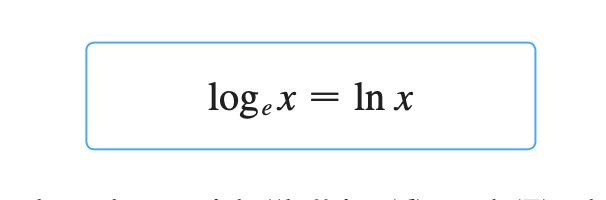
Defining Properties of the Natural Logarithmic Function

Change in Base Formula

The Change-of-Base Formula lets you rewrite a logarithm in any base using logs of another base.

Why is it difficult to find Inverse Trigonometric Functions ?

When we try to find the inverse trigonometric functions, we have a slight difficulty:

Because the trigonometric functions are not one-to-one, they don’t have inverse functions. The difficulty is overcome by restricting the domains of these functions so that they become one-to-one.

Inverse sine Function

The inverse of the sine function is called the arcsine function,

written as:

sin⁡−1(x) or arcsin⁡(x)

Definition:

y=arcsin⁡(x)⟺sin⁡(y)=x

So the arcsine function undoes the sine function.

The Inverse Cosine Function

The inverse cosine function is called arccosine, written as

cos⁡−1(x) or arccos⁡(x)

Definition: y= arccos⁡(x)⟺cos⁡(y)=x

So the inverse cosine function undoes the cosine function.

Inverse Tangent Function

The inverse tangent function is called arctangent, written as

tan⁡−1(x) or arctan⁡(x)

Definition: y=arctan⁡(x)⟺tan⁡(y)=x

So the inverse tangent function undoes the tangent function