Chapter 18 - Geometry

What is the difference between lines, rays, and line segments?

• line: extends infinitely in both directions

• ray: a line that only extends from 1 of its points

• line segment: line that ends at both directions

How do you name lines, rays, and line segments?

** for rays, you can only name them in one direction. the endpoint is the first letter. it must be AB

lines and line segments can go either way AB or BA

acute angle

angle less than 90 degrees

obtuse angle

greater than 90 degrees, but less than 180 degrees

What do the interior angles of a triangle add up to?

180 degrees

Equal sides of a triangle means…

the angles are equal

The longest side of the triangle is located…

across from the biggest angle

Given any polygon, what happens when you add up all the exterior angles at each vertex?

The sum of the measures of exterior angles will always equal 360

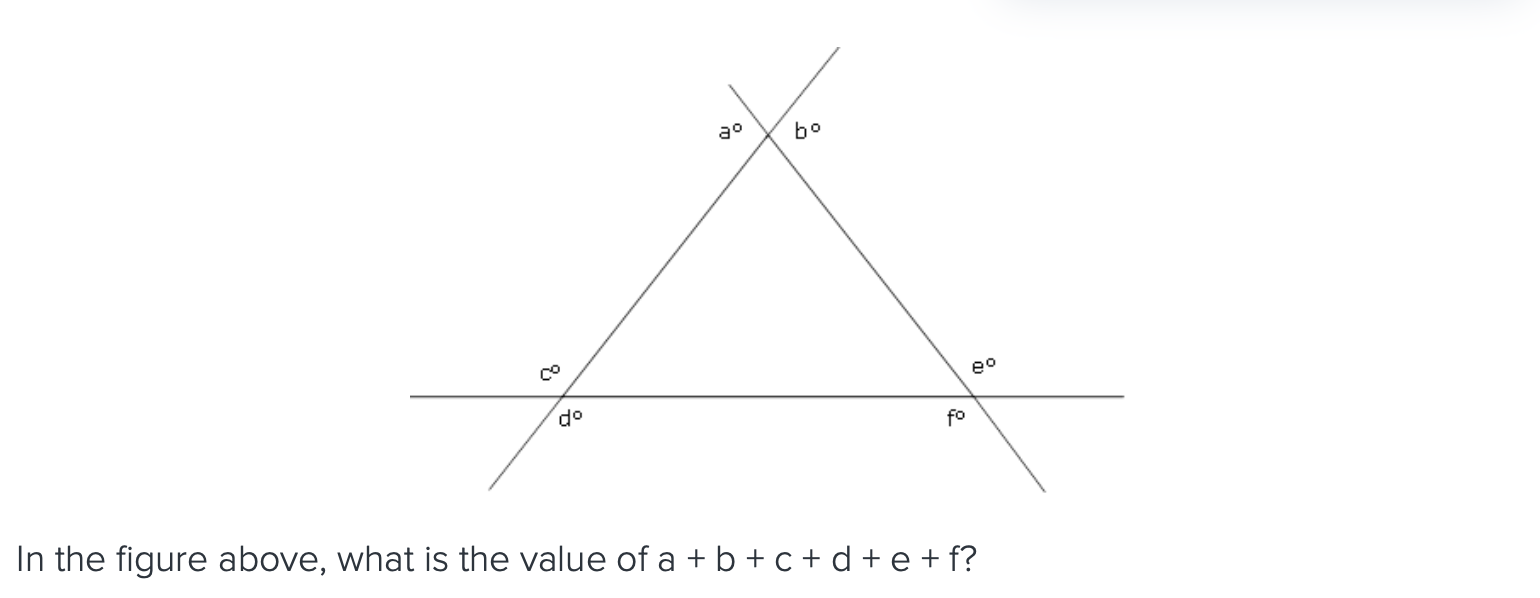
720 degrees

the sum of the exterior angles of a polygon equal to 360 when you draw 1 line from a vertex

since you have 2 lines coming our from each vertex, you would calculate (2)(360) =720 720

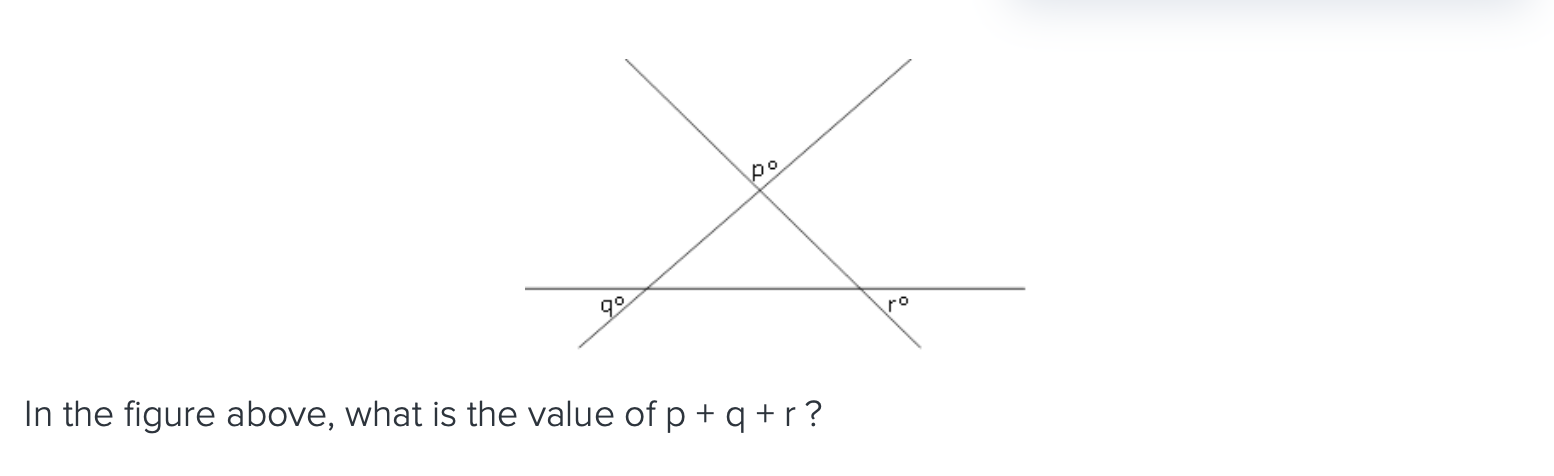
these angles are not exterior angles which is why they don’t sum to 360 degrees

An exterior angle of a triangle is equal to….

the sum of its 2 remote interior angles

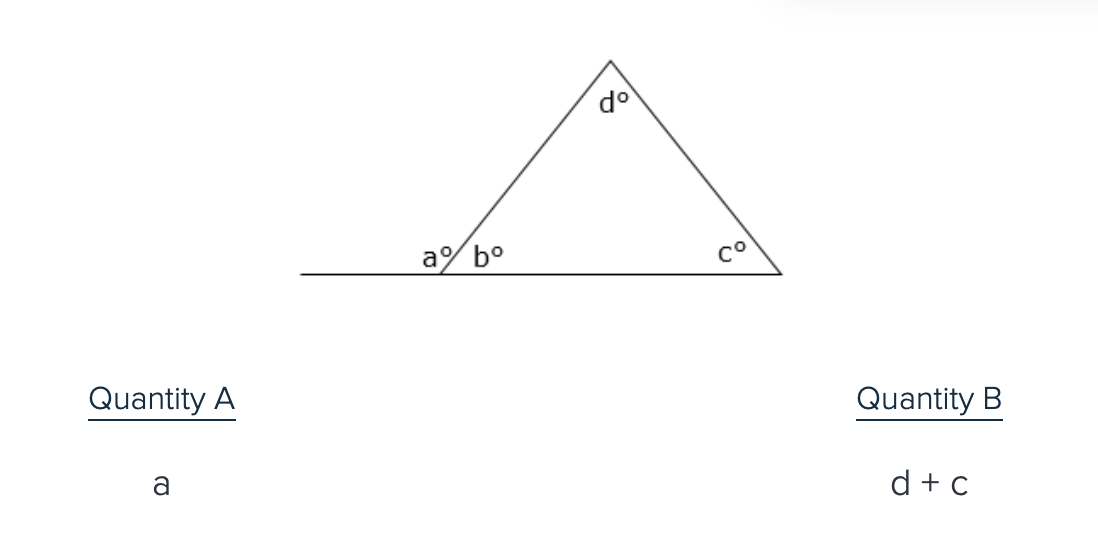
The 2 quantities are equal

An exterior angle of a triangle is equal to the sum of its 2 remote interior angles

What’s the area of a triangle?

(½ )(base)(height)

height is always perpendicular to the base of the triangle

What do you know about sums/difference of the lengths of the sides of triangles?

1. In any triangle, the sum of the lengths of any two sides of the triangle is greater than the length of the third side

2. In any triangle, the difference of the lengths of any two sides of the triangle is less than the length of the third side

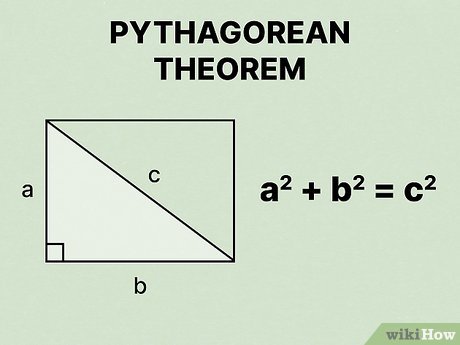
How do you find the hypotenuse of a right triangle?

Use the Pythagorean theorem

Let c be the hypotenuse
c² = a² + b²

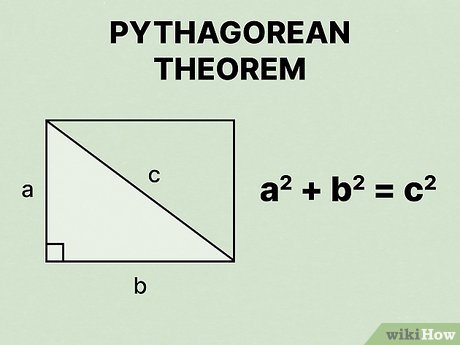
Given any triangle with sides a, b, and c, if c² = a² + b², then what must you know about the sides of the triangle?

the side opposite side C must measure 90 degrees and thus the triangle must measure 90 degrees

What are 2 Pythagorean triples?

1. 3-4-5

   • 3² + 4^{2 =} 5²

   • look for other ratios of this: {6, 8, 10}, {9, 12, 15}

2. 5-12-13

   • 5² + 12^{2 =} 13²

   • look for other ratios of this: {10, 24, 26}, {15, 36, 39}

if you see any of these side lengths of a triangle, you know the other dimensions

What is the formula to find the area of an isosceles triangle?

l²/2 = (leg₁)(leg₂)/2

let l be the length of one of the equal sides

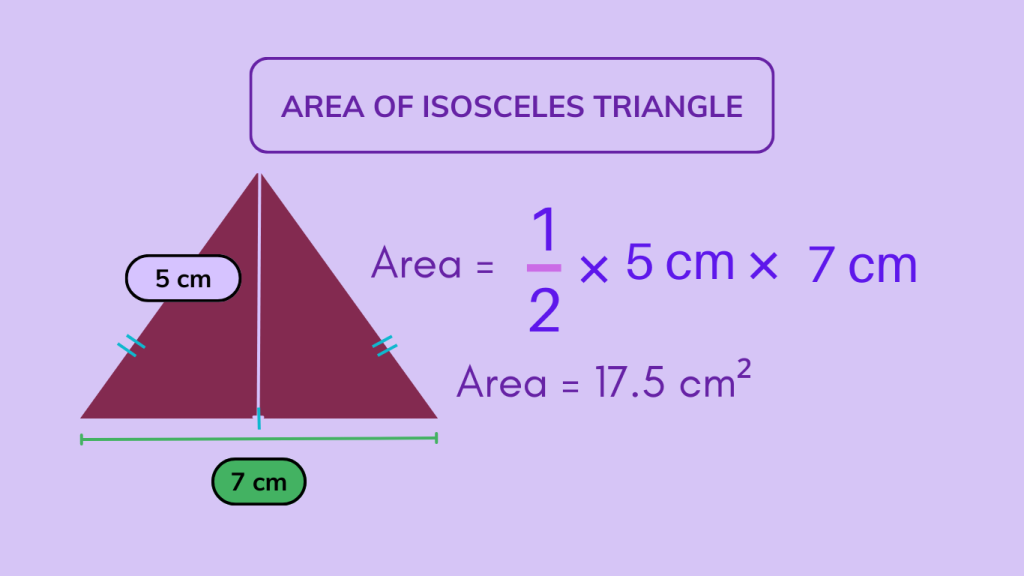
What are the angles in an isosceles triangle?

90-45-45

2 even shorter sides, 1 long side

How do you find the length of the sides of an isosceles 90-45-45 right triangle?

they’re in this ratio: x : x : x√2

the longer side will always be multiplied by √2

What are the lengths of the sides of a 30-60-90 triangle?

the ratio of the sides is: x, x√3, 2x

• x is the side opposite the 30 degree angle

• x√3 represents the length of the side opposite the 60 degree angle

• 2x represents the side opposite the 90 degree angle

If an isosceles triangle is in a square, how do you find the area?

the area is ½ of the size of the square that they form

What shape do the diagonals of a square cut into?

• It forms 2 diagonal isosceles triangles

• the area of a square is equal to 2 isosceles right triangles

  • 45-45-90

What’s the formula for finding the area of equilateral triangle?

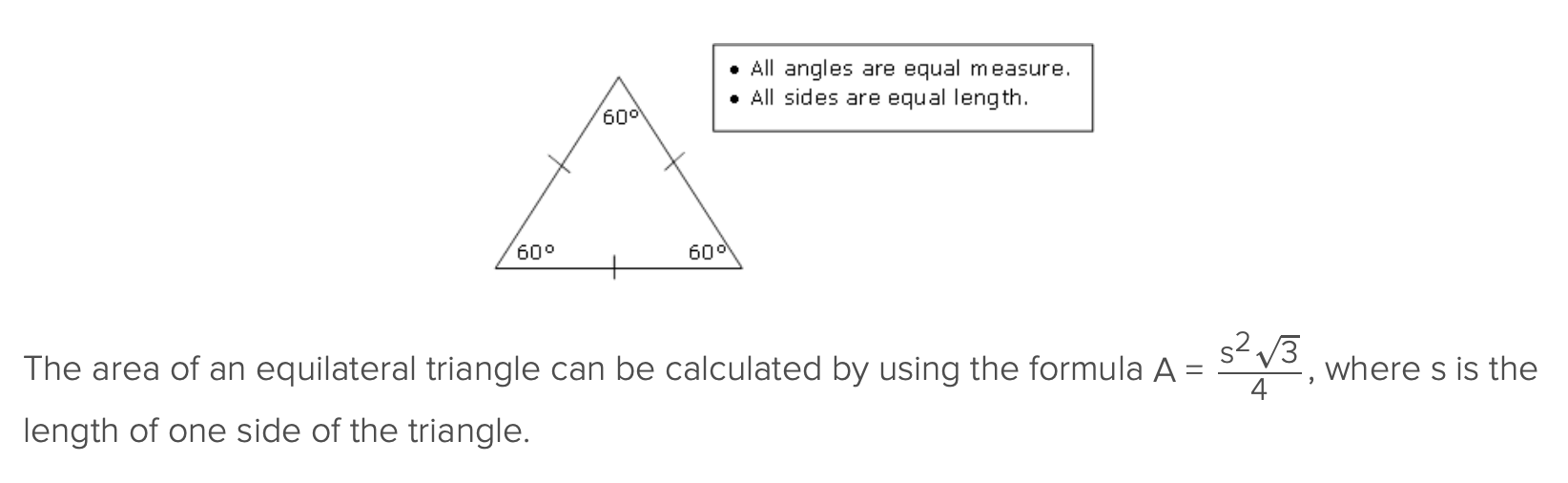
What happen when you split an equilateral triangle in two? specifically dropping a height line?

it will create identical 30-60-90 triangles

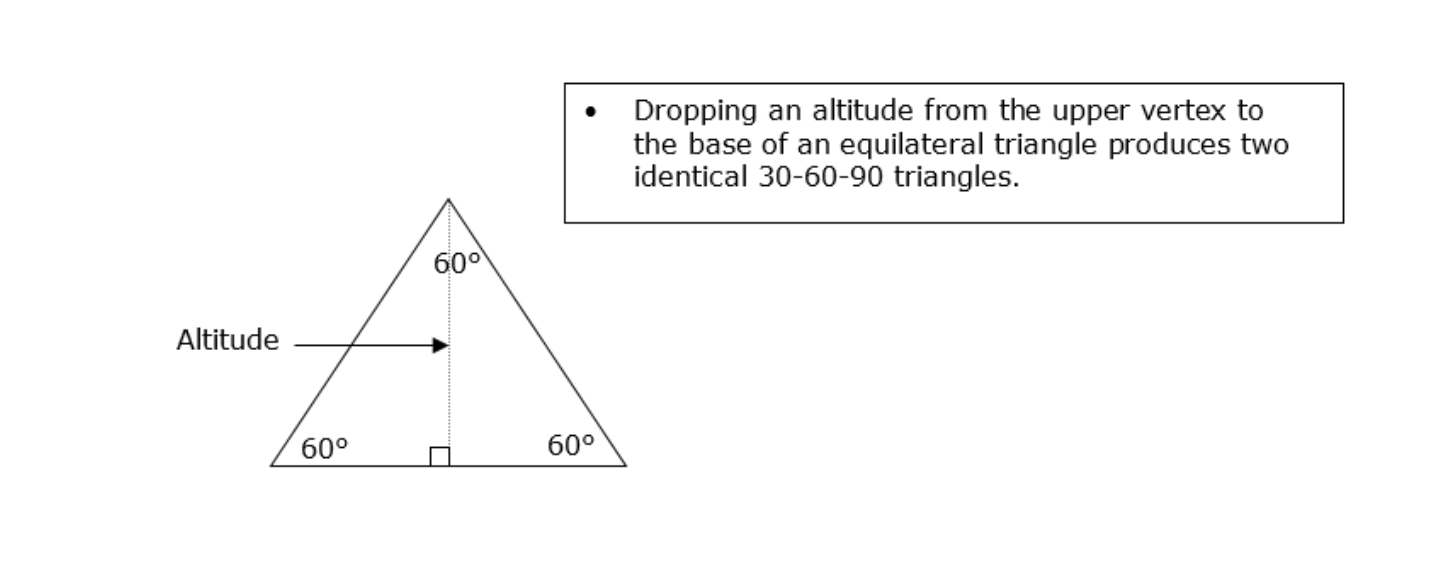
What are the 3 cases that triangles are similar

1. the 3 angles measure the same 3 angles as the other triangle

2. 3 corresponding sides have the same lengths or ratios

3. the angle of one triangle is the same as another and the other 2 sides are the same

All rectangles can geometrically categorized as what shape?

parallelograms

What is true about the angles in a parallelogram?

1. adjacent angles sum to 180 degrees

2. all opposite angles are equal in measure

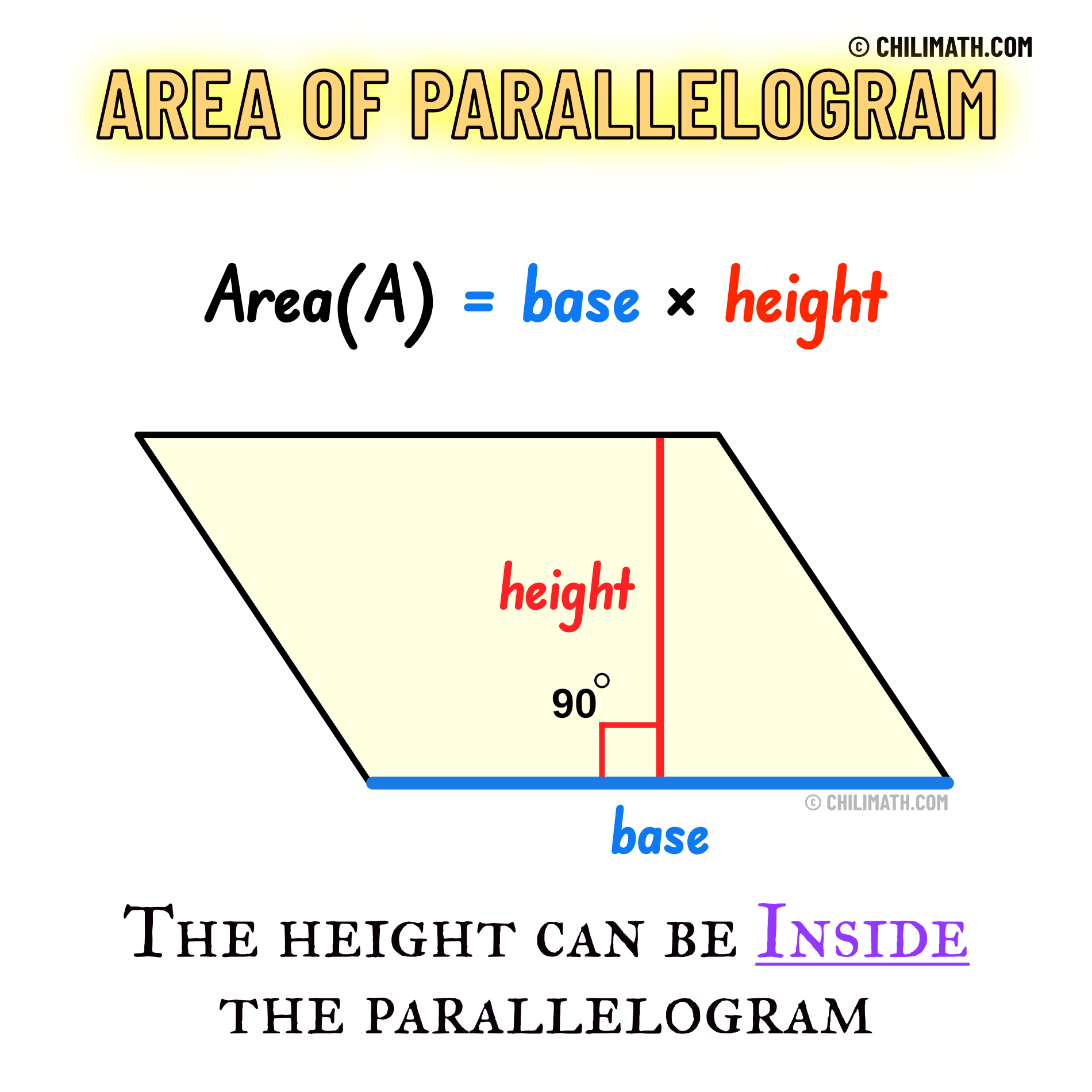
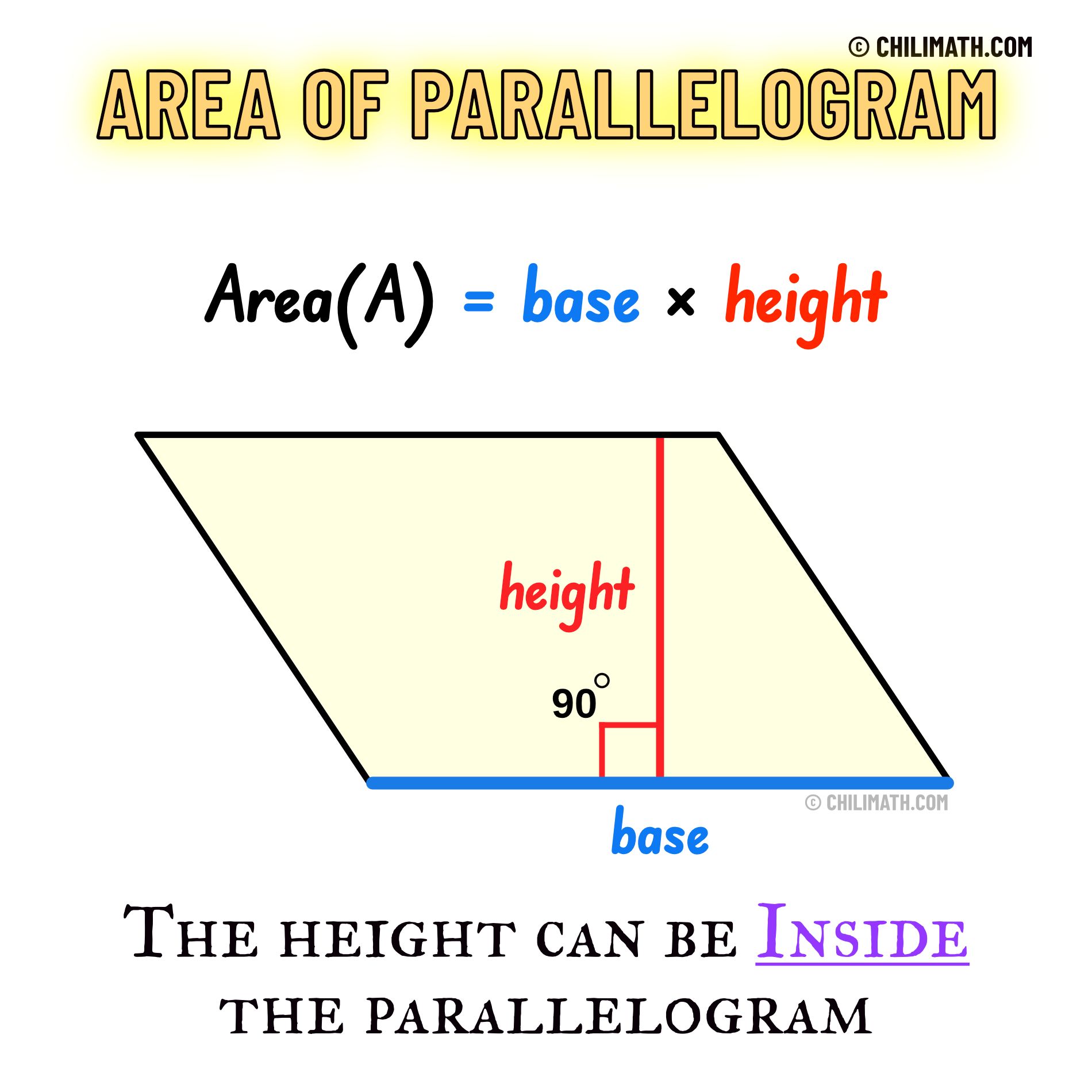
What is the formula for the area of a parallelogram?

area = base x height

What is the formula for the perimeter of a rectangle?

2l + 2w

What do we know about diagonals in rectangles?

• the longest line segment that can be drawn in a rectangle can be its diagonal 

• the diagonal is equal to √l² + w²

• each diagonal is the same length and bisects each other (divides it in 2)

• the diagonals also divide the rectangle into 2 right triangles 

• this diagonal may not split the rectangle into be a 30-60-90 diagonal. each rectangle is slightly different

What shapes can you make from a regular hexagon?

A regular hexagon can be divided into 6 equilateral triangles

If you add up all the exterior angles of a polygon, what will they sum to?

always add up to 360°

What do you know about the diagonals of squares?

• the length of a square’s diagonal is √2

• each diagonal divides the square into two 45-45-90 right triangles 

• The diagonals of squares are perpendicular 

• the diagonals bisect each other, meaning they’re all the same length 

If a group of rectangles has the same perimeter dimensions, what is the shape of a the rectangle has the maximum area?

The rectangle with the maximum area is a square 

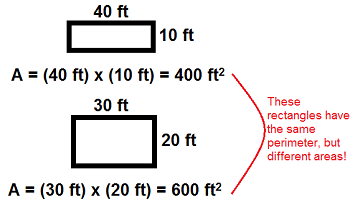
Given a group of rectangles, which rectangle has the minimum perimeter?

a square

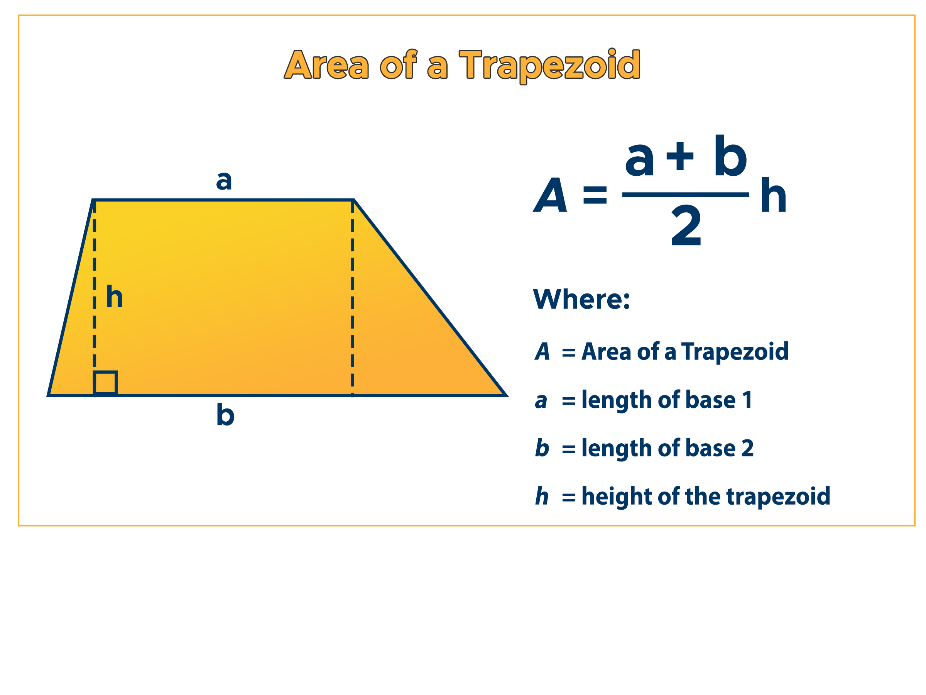
What is the formula for the area of a trapezoid?

(½)(base₁ + base₂) ( height)

How do you find the sum of the interior angles of a polygon?

(n-2) * 180

What is a regular polygon?

when all the sides of the polygon are of equal length and all the angles are of equal measure 

What is the formula to find the measure of one interior angle of a regular polygon?

(180(n-2))/n

where n is the number of sides of the polygon

What do you know about the interior angles of hexagons?

• the sum of the interior angles of any hexagon is 720 degrees

• any one interior angle of a regular hexagon measures 120 degrees 

What’s the area of a regular hexagon?

you can approximate the formula as 2.6s² to save time 

alternate formula:

if you know the distance between any parallel sides of the hexagon and the length of the side is known 

area = 1.5ds

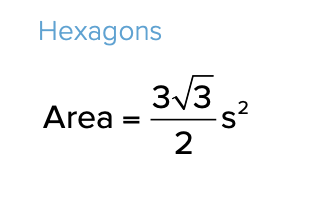
What is the sum of the exterior angles of an octagon?

360°

all exterior angles of any polygon add up to 360°

you make an exterior angle by extending a line from one of the polygons sides

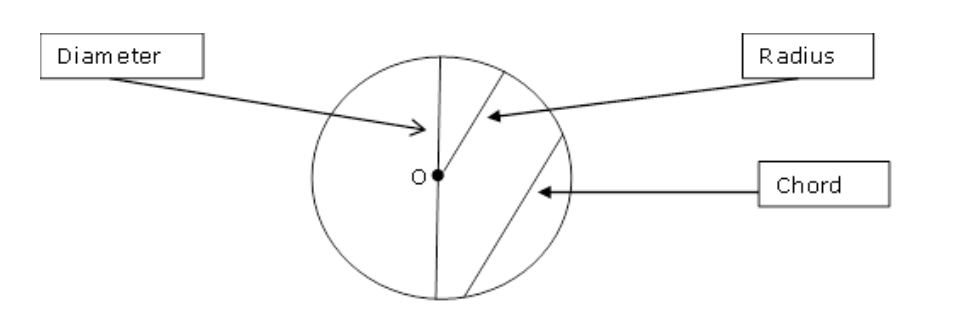
What is a chord in a circle?

• a line segment that connects any 2 points on the circle

• if a chord passes through the center of the circle, that’s the diameter 

Circumference formula?

• option #1: 2πr

• option #2: πd

• you can use 3 to estimate for π

• if π is present in the calculations, carry pi through the equation 

Area of a circle?

πr²

What do you know about the arc length and the area of a circle?

everything is proportionally related (refer to screenshot)

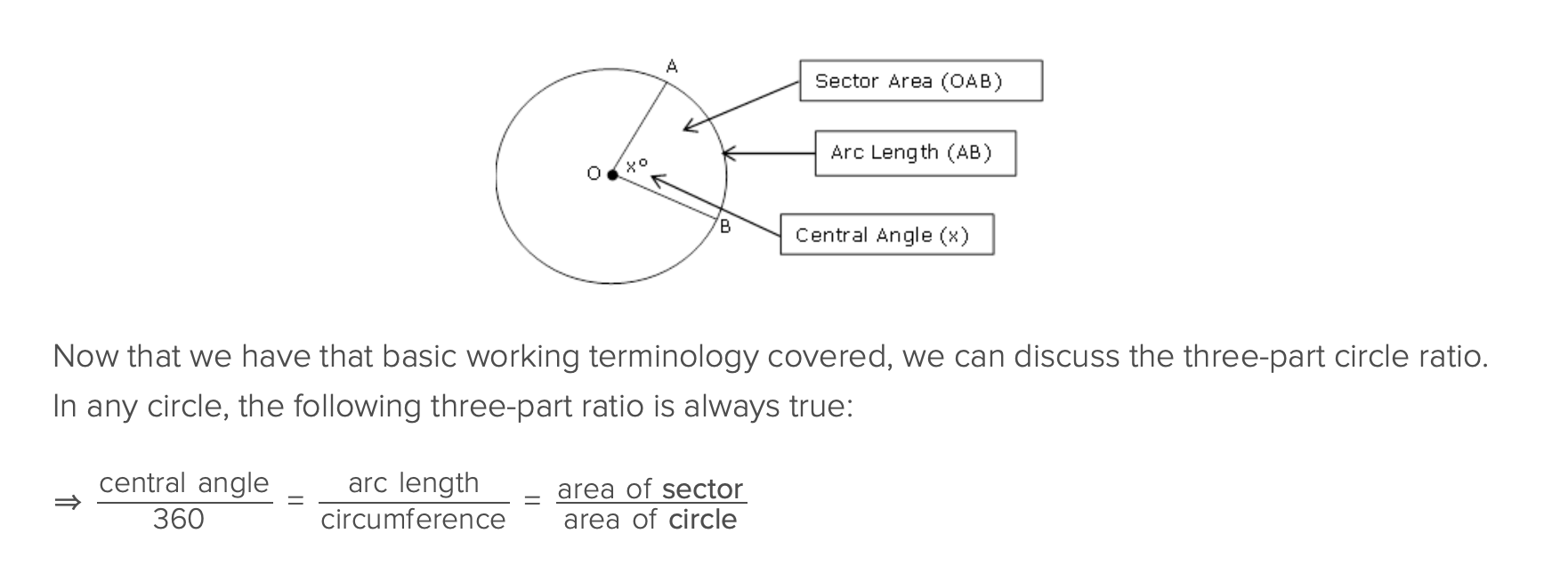
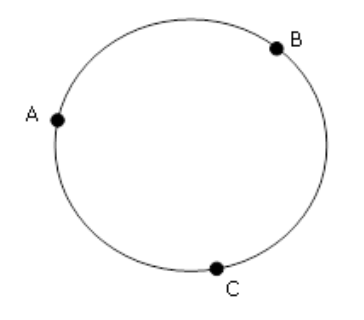
What do you know about major and minor arcs in a circle?

• If points A and B are on a circle and arc AB is not a semicircle then arc AB refers to the shorter arc between A and B 

• the shortest portion is also known as the minor arc 

• the longer portion of the circumference AB and would be known as arc ACB

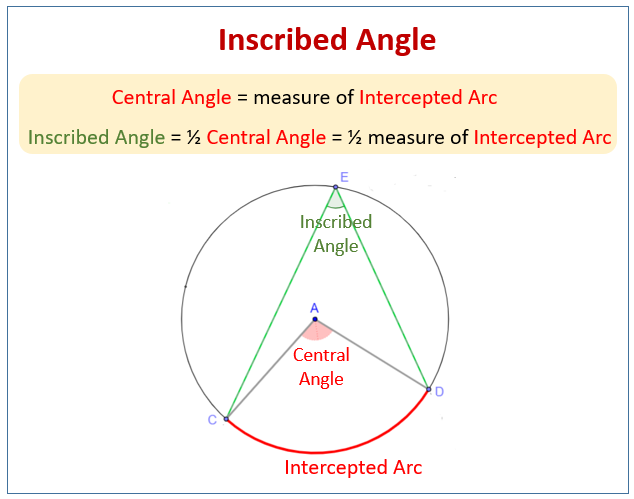
How do you know the degrees of an inscribed angle?

• the degree of an inscribed angle is equal to half the degree measure it intercepts

• if the inscribed angle share the same points as the central angle, that inscribed angle is twice the degree of the central angle 

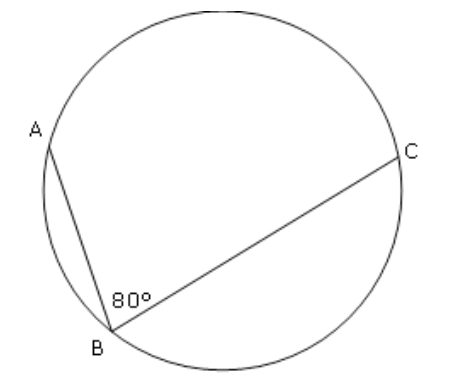
In the figure above, what is the degree measurement of arc AC?

160 

• angle ABC is an inscribed angle 

• that means that the measure of the angle ABC is one half the measure of arc AC

• the measure of arc AC is 2 × 80 =160 160

How do you calculate the longest line segment that can be drawn in a cube?

you would need to find the diagonal that starts at one corner and ends at the other

• d = s√3

• where s is one length of one side of the cube 

How do you know if the triangle inscribed in a circle is right triangle?

if one side of the triangle is the diameter

If the hypotenuse of an inscribed triangle is the diameter of the circle, then…

the triangle is a right triangle

When an equilateral triangle is inscribed in a circle…

the center of the circle is the center of the triangle

if you draw a line from the center of the circle to a vertex of the triage, the line segment would be

1. a radius of the circle

2. it would also bisect the 60 degree angle (it would become 30 degrees)

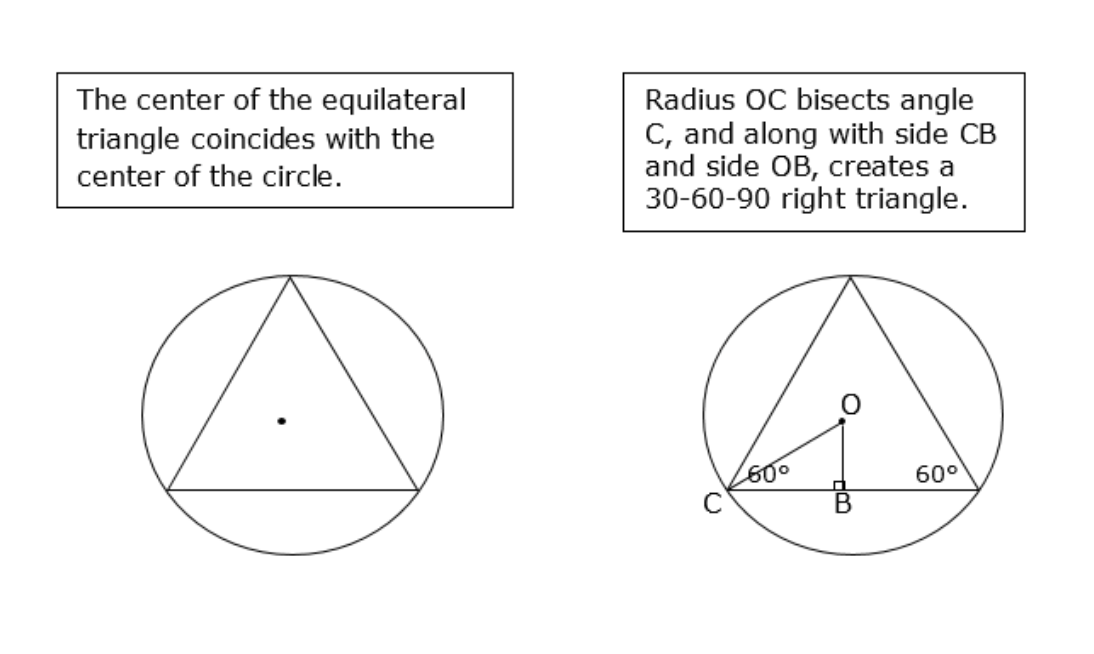
What does it mean when you have an equilateral triangle inscribed in a circle?

The triangle divides the circumference of the circle into 3 different equal arc lengths

*if you know the length of any of these arcs, you can easily find the circumference

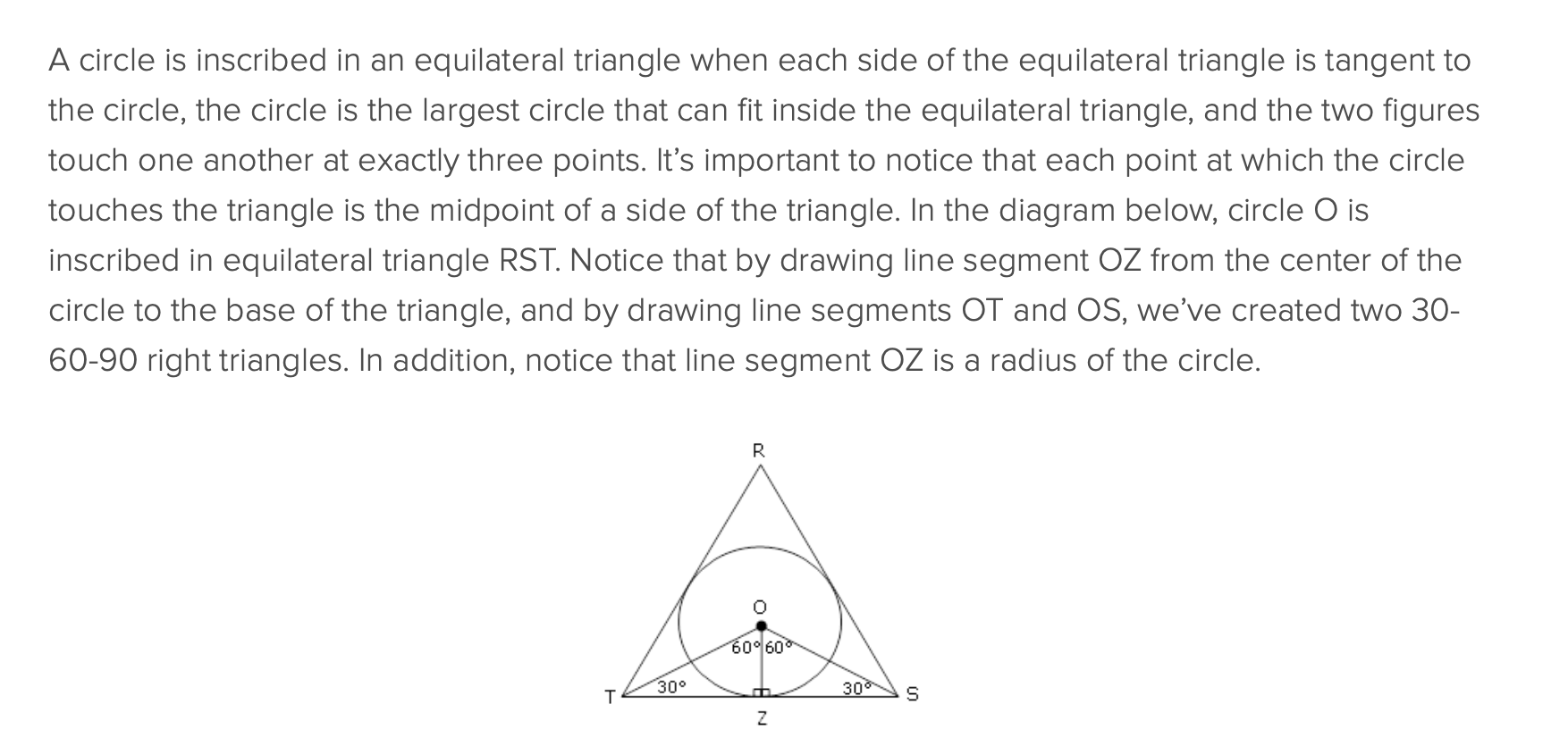
How do you know if a circle is inscribed inside a triangle?

1. When each side of the equilateral triangle is tangent to the circle

2. the circle is the largest that can fit inside the equilateral triangle

3. the 2 figures touch each other exactly at 3 points

What do you know about squares that are inscribed in circles?

The diagonal of the square is also the diameter of the circle

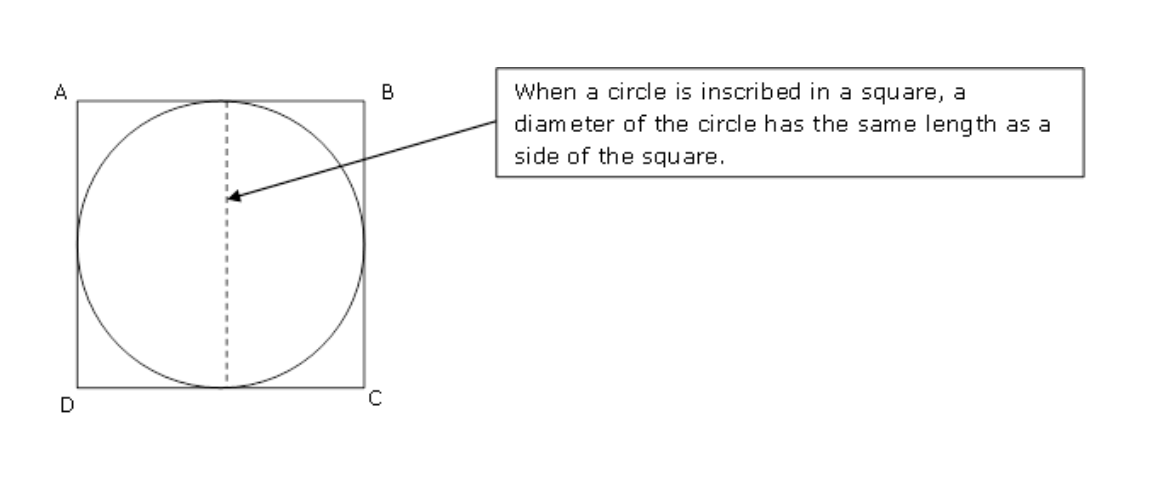
What does it mean when a circle is inscribed in a square? and how do you know a circle is actually inscribed?

The diameter of the circle has the same length as the side of the square

But the circle must actually be inscribed in the square meaning:

1. each side of the square is tangent to the circle

2. the 2 figures touch exactly at 4 points

3. each point at which the circle touches the square is the midpoint of that square’s side

What do you know when a rectangle is inscribed in a circle?

The diagonal of the rectangle is also the diameter of the circle

NOTE: you can’t assume that the rectangle will make a 30-60-90 triangle

the ratio of the shorter side to the longer side would need to be x : x√3

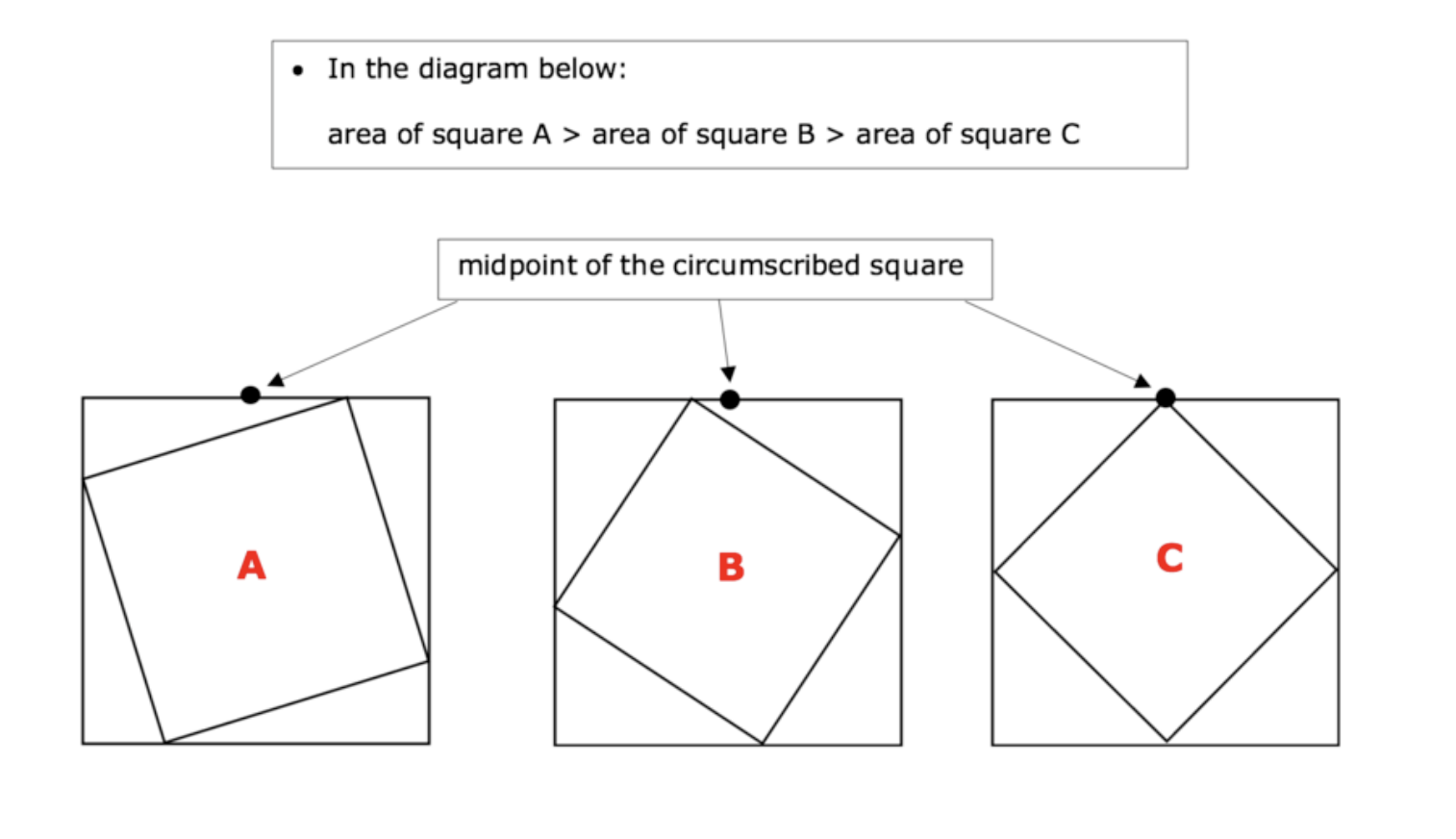
What’s the difference between and inscribed square and a circumscribed square?

inscribed square: all 4 vertices of the inscribed square are touching all 4 respective edges of the another, bigger square (the circumscribed square)

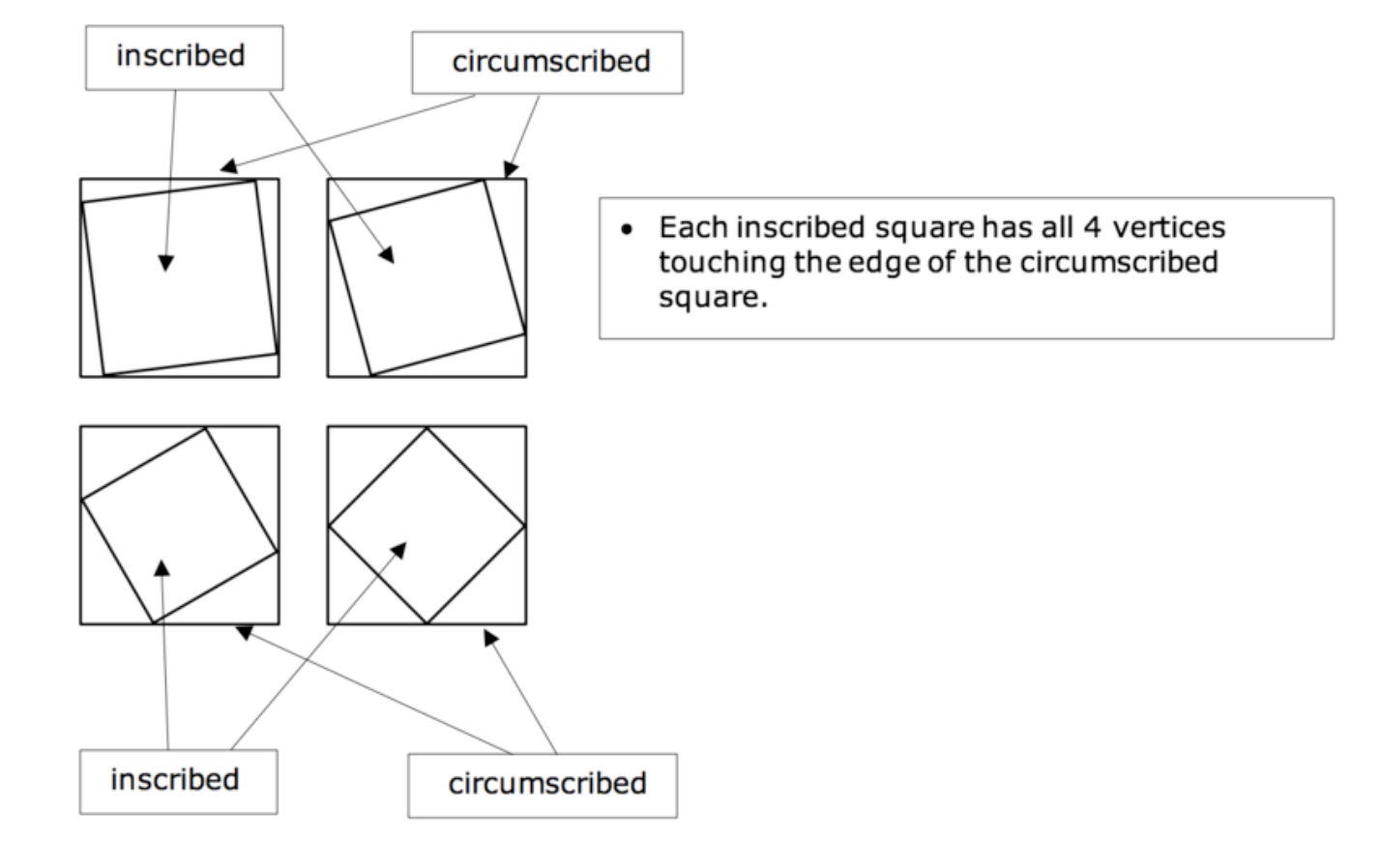
When will the area of an inscribed circle be the smallest?

when the vertices of the square are the closet to the midpoints of the respective edges of the squares

• the area of the square inscribed exactly on the midpoints of the bigger circumscribed square  will have an area that’s exactly ½ that of the bigger square 

How do you approach a problem when a rectangle is inscribed in a semi-circle?

1. you need to create a right triangle 

   • draw a radius from the center of the circle to a vertex of the rectangle 

2. the height of this triangle = side of the rectangle 

   • if the width of the rectangle is x, then height of the of the triangle is x

3. the length of the rectangle = 

   • if the length of the rectangle is x, then the base of the triangle is ½x

What happens when a regular polygon is inscribed in a circle?

When a regular polygon is inscribed in a circle, the polygon divides the circle in arcs of equal length 

what is a uniform border?

a border of entirely equal width that surrounds an object 

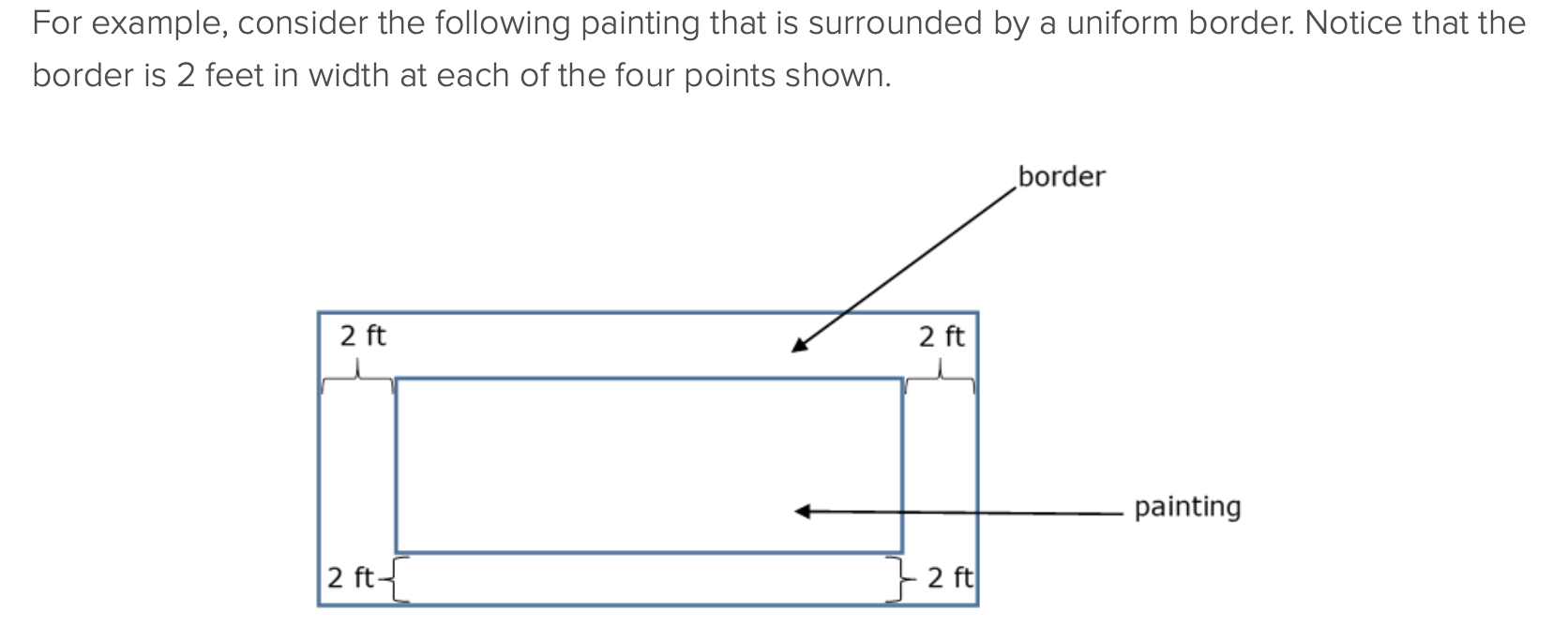
How to approach uniform border questions?

What is the volume of a right circular cylinder?

V = πr²h

How do you calculate the areas in a 2 circle system?

π((R₂)² - (R₁)²)

R₁ is the radius of the inn circle

R₂ is the  radius of outer circle

How do find the longest line segment that can be drawn in a within a rectangular solid?

• the longest line segment that can be drawn within a rectangular solid is the diagonal that goes from the corner of a the box or cube through the center of the box or cube to the opposite corner 

• use the extended Pythagorean theorem to find the longest diagonal

  • d² = l² + w² + h²

What is the surface area of a right cylinder?

2(πr²) + 2(πrh)

How do you approach problems that ask you that deals with the rate at which volume of a container is being filled?

time is usually t = distance / rate

but when using 3d shapes then you would do

t = (volume of container) / rate

What do you need to know in order to determine the rate at which a liquid will rise in a 3d object?

you need to know 2 things

1. the rate at which the liquid flows into the figure

2. the exact dimensions of the figure 

You have a rectangular box with a volume of 1000 cm³. The water is flowing in to the box at a rate of 10cm³ per minute. How high would the water in the box be after 10 minutes?

many different combinations of length, width, and height can produce 1000cm³, you can’t determine based on the volume, how high the water would be 

If you have a box with a volume of 36 cm³, how many smaller boxes (each with 6 cm³ volume) would fit in the larger box?

• its not possible to know

• depending on the dimension of the boxes, they’ll fit next to each other differently

• you would need to know the exact dimension of the bigger and smaller box

How do you determine the number of smaller objects that will fit within a larger object of known volume?

You must know

1. the exact dimensions of the bigger object

2. the exact damsons of the smaller object

What happens when happens when you cut an equilateral triangle in half?

You get 2 identical 30, 60, 90 triangles

In a circle with the circumference of C, if an arc length L is inscribed by a central angle of x degrees, then x/360 =

L/C

In a circle with area A, if a sector of area S is inscribed by a central angle of x degrees, then x/360 = 

S/A

If inscribed angle of S degrees intercepts a central angle of C degrees, then S =

C/2

If inscribed angle of S degrees intercepts a central angle of C degrees, then C =

2S

When a regular polygon is inscribed in a circle, the polygon divides the circle into…

arcs of equal lengths

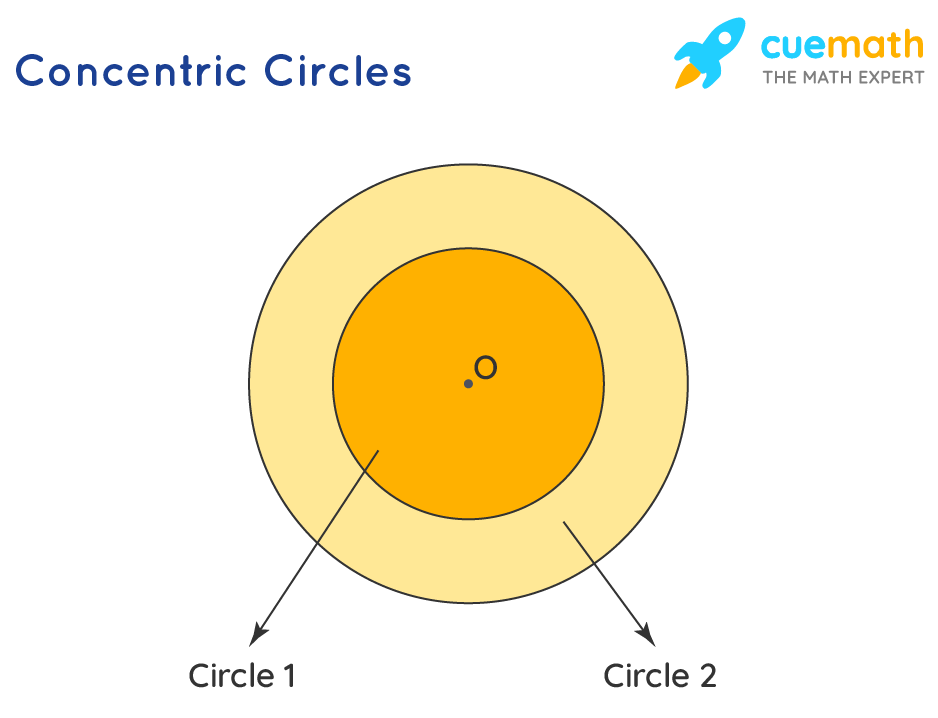
How do you find the area of a concentric circle system (shown in pic) where the radius of the inner ring is R₁ and the radius of the outer rings is R₂, the area of the outer ring is…

π[(R₂)² - (R₁)²]

The surface area of a cube with side length s is…

6s²

What’s the surface area of a rectangular solid with length L, width W, and height H?

2(W x L) + 2(W x H) + 2(L x H)

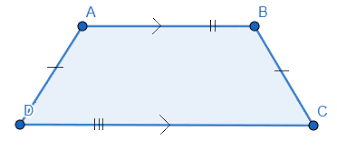
What is an isosceles trapezoid?

a trapezoid in which the 2 non-parallel sides are equal in length