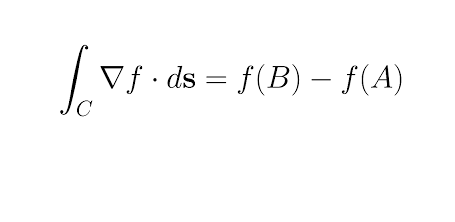Midterm 4 Practice
0.0(0)
0.0(0)
Card Sorting
1/27
Earn XP
Study Analytics
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
28 Terms
1
New cards
If F is a vector field, then div F is a vector field. True or False
False: div F results in a scalar function
2
New cards
If F is a vector field, then curl(F) is a vector field.
True: curl(F) results in a vector function
3
New cards
If f has continuous partial derivatives of all orders on ℝ3, then div(curl(∇f)) = 0.
True:
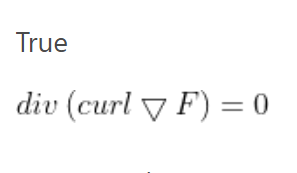
4
New cards
If f has continuous partial derivatives of all orders on ℝ3 and C is any circle, then
∫∇f · dr = 0.
∫∇f · dr = 0.
TRUE:
if function is continuous and derivatives exist then line integral in a closed path is zero
if function is continuous and derivatives exist then line integral in a closed path is zero
5
New cards
If
F = P i + Q j
and
Py = Qx
in an open region D, then F is conservative.
F = P i + Q j
and
Py = Qx
in an open region D, then F is conservative.
FALSE:
To satisfy the conservative property, the region D should be open AND simply connected
To satisfy the conservative property, the region D should be open AND simply connected
6
New cards
FALSE
7
New cards
If F and G are vector fields and div F = div G, then F = G
FALSE: Check this counter-example
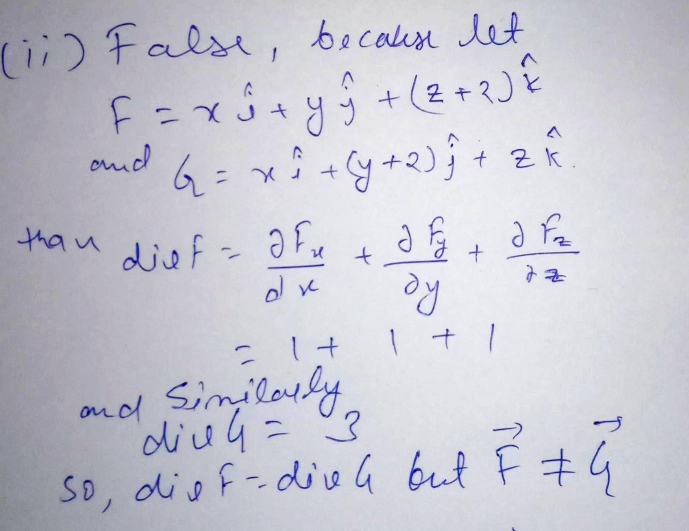
8
New cards
The work done by a conservative force field in moving a particle around a closed path is zero.
TRUE:
A force is conservative exactly when the work it does on an object is zero for every possible closed path the object can take.
A force is conservative exactly when the work it does on an object is zero for every possible closed path the object can take.
9
New cards
If F and G are vector fields, then
curl(F + G) = curlF + curlG
curl(F + G) = curlF + curlG
TRUE:
Try an example!
Try an example!

10
New cards
If F and G are vector fields, then
curl(F · G) = curlF · curlG
curl(F · G) = curlF · curlG
FALSE:
Intuitively, you can see this will be false because F · G = scalar.
curl is defined for vectors only
Intuitively, you can see this will be false because F · G = scalar.
curl is defined for vectors only
11
New cards
If S is a sphere and F is a constant vector field, then
∫∫s F · ndS = 0
∫∫s F · ndS = 0
TRUE:
∫∫s F · ndS = ∫∫∫v div F dudydz
if F is constant then div F = 0
therefore, ∫∫d F · ndS = 0
∫∫s F · ndS = ∫∫∫v div F dudydz
if F is constant then div F = 0
therefore, ∫∫d F · ndS = 0
12
New cards
There is a vector field F such that curl(F) = xi + yj + zk
FALSE:
Every vector function G satisfies the property:
div(curlF) = 0
if curl(F) = xi + yj + zk, then div(curl(F)) = 3
Since this results in a non zero scalar, the statement is false
Every vector function G satisfies the property:
div(curlF) = 0
if curl(F) = xi + yj + zk, then div(curl(F)) = 3
Since this results in a non zero scalar, the statement is false
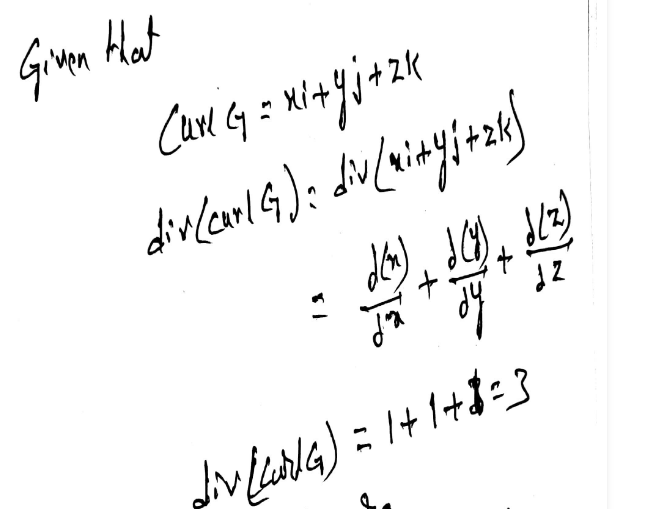
13
New cards
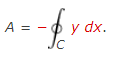
The area of the region bounded by the positively oriented, piecewise smooth, simple closed curve C is
A= - ∮c ydx
A= - ∮c ydx
TRUE:
The area pf the region bounded by positively oriented, piecewise smooth, simply closed curve C can be represented with
A= ∮c ydx
and A= ∮c ydx = - ∮c ydx
The area pf the region bounded by positively oriented, piecewise smooth, simply closed curve C can be represented with
A= ∮c ydx
and A= ∮c ydx = - ∮c ydx
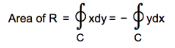
14
New cards
is curl(f) a ...
a) scalar field
b) vector field
c) not meaningful
a) scalar field
b) vector field
c) not meaningful
c) not meaningful
15
New cards
is grad(f) a ...
a) scalar field
b) vector field
c) not meaningful
a) scalar field
b) vector field
c) not meaningful
b) vector field
16
New cards
(F is a vector function)
is div(F) a ...
a) scalar field
b) vector field
c) not meaningful
is div(F) a ...
a) scalar field
b) vector field
c) not meaningful
a) scalar field
17
New cards
is curl(grad(f)) a ...
a) scalar field
b) vector field
c) not meaningful
a) scalar field
b) vector field
c) not meaningful
b) vector field
18
New cards
is grad(F) a ...
a) scalar field
b) vector field
c) not meaningful
a) scalar field
b) vector field
c) not meaningful
c) not meaningful
19
New cards
is grad(div(F) a ...
a) scalar field
b) vector field
c) not meaningful
a) scalar field
b) vector field
c) not meaningful
c) vector field
20
New cards
is div(grad(f)) a ...
a) scalar field
b) vector field
c) not meaningful
a) scalar field
b) vector field
c) not meaningful
a) scalar field
21
New cards
is grad(div(f)) a ...
a) scalar field
b) vector field
c) not meaningful
a) scalar field
b) vector field
c) not meaningful
c) not meaningful
22
New cards
is curl(curl(F)) a ...
a) scalar field
b) vector field
c) not meaningful
a) scalar field
b) vector field
c) not meaningful
b) vector field
23
New cards
is div(div(F)) a ...
a) scalar field
b) vector field
c) not meaningful
a) scalar field
b) vector field
c) not meaningful
c) not meaningful
24
New cards
is (grad(f)) x (div(F)) a ...
a) scalar field
b) vector field
c) not meaningful
a) scalar field
b) vector field
c) not meaningful
c) not meaningful
25
New cards
is div(curl(grad(f))) a ...
a) scalar field
b) vector field
c) not meaningful
a) scalar field
b) vector field
c) not meaningful
a) scalar field
26
New cards
If all the component functions of F have continuous partials, then F will be conservative if
curl(F) = 0
27
New cards
A vector field G exists in R^3 if...
div(curl G) = 0
28
New cards
Fundamental Theorem of Line Integral