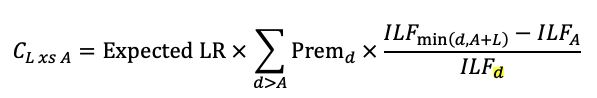EXAM 5 SECTION C

risk classification

grouping risks w/ similar risk characteristics (expected costs) for purpose of setting prices

adverse selection

• Insurer not using risk characteristic used by competitors

• Competitors will attract lower risk insureds

• While insurer left w/ higher than proportional share of higher risks

  • High risks undercharged → unprofitable

favorable selection

when you recognize risk char not recognized by competitor

Strategy: raise rates for low risks to be just below competition’s

• so they’ll still move over to your company AND maximize profit!

proxy underwrite accept market

What if a rating variable is prohibited?

• Find correlated _____ variables and rate based on those

• Can still _____ based on the risk char to only _____ lower risk insureds

• _____ to lower risk insureds & avoid marketing to higher risk

skimming the cream uw marketing

_____: insurer uses a risk characteristic in _____ or _____ to attract lower cost risks WITHOUT lowering prem!

• Protects insight from competitors

  • Rates have to be made publicly available

  • UW guidelines don’t

significance homogeneity credibility objective expense verifiable affordability causality controllability privacy

Criteria for Rating Variables:

1. Statistical Criteria

   1. Statistical _____

   2. _____

   3. _____

2. Operational Criteria

   1. _____

   2. _____

   3. _____

3. Social Criteria

   1. _____

   2. _____

   3. _____

   4. _____

4. Legal Criteria

statistical significance expected costs homogeneity individ class subclasses loss potential credibility large

Statistical Criteria for Rating Var

_____ _____: _____ _____ should vary by class w/ acceptable lvl of stat confidence

_____: expected costs for _____ risks within _____ should be similar

• No clearly identifiable _____ w/ significantly diff _____ _____

_____: classes _____ enough to allow cred statistical predictions

• But a class doesn’t need to be fully credible on its own

operational objective measurable defined expense obtaining verifiable manipulate

_____ Criteria for Rating Var

_____: classes are _____ & clearly _____; exhaustive & mutually exclusive

_____: cost of _____/maintaining data not too high

_____: easily verifiable, hard to _____

social affordability negative causality intuitive acceptance controllability chance privacy

_____ Criteria for Rating Var

_____: esp a problem when there’s _____ correlation between income & rates

_____: _____ relationship between rating var & cost

• Increases public _____

_____: encourages insureds to reduce _____ of loss for lower rate

• Increases public acceptance

_____: not too intrusive

legal

_____ Criteria for Rating Var

• in compliance w/ local laws & regulations

exposure

Overall Rate Indications → overall avg rate for book

Class Relativities → relative costs between classes

• Univariate Analysis

• Multivariate Analysis

  • Preferred bc correctly adjusts for _____ correlation

simple correlation OL levels rels

Univariate Pricing Approaches:

1. PP Approach

   • Pro: _____

   • Con: least accurate when there’s exposure _____

2. LR Approach

   • Pro: partially corrects for exp corr

   • Con: requires _____ prem by _____ of var

3. Adjusted PP Approach

   • Pro: partially corrects for exp corr

   • Con: cumbersome to calculate wtd-avg _____ for many variables

   • ***Identical results as LR Approach!

exposure correlation

exposures of levels of X1 are correlated w/ exposures of levels of X2

• “double counts” experience of correlated variables

exposures at base adj exposures rebase

Univariate Pricing Approaches w/ Credibility

• Need ind rel & complement to be on same basis!

  • Ind Rel to Total

  • Normalized Complement

• Make them relative to a WEIGHTED total

  • PP → weigh by earned _____

  • LR → weigh by prem _____

  • Adj PP → weigh by _____

• Don’t forget to _____!

pp

Univariate Pricing approach → _____

Ind Rel = PP_class / PP_base

lr prem at base olep curr rel

Univariate Pricing approach → _____

Ind Rel Chg Factor = LR / Total LR

Ind Rel = Curr Rel x Chg Factor

SHORTCUT: Cred Complement is Current Rates

• Weigh Chg Factor with 1!

Other complements → weigh rels by _____

• calculate relativities first then weigh

• Prem at Base = _____ / _____

adj pp

Univariate Pricing approach → _____

• For each level of a variable:

  • Adj Exp = EE wtd by Curr Rel of Other Var

sequential analysis

sequence of using Adj PP Approach

• Pro: partially corrects for exp correlation

• Con: order matters

Steps

1. Perform univariate analysis to get ind rel for Var1

2. Use Var1 ind rels to adjust exp for Var2

   1. Apply Adj PP approach

3. Use Var2 ind rels to adjust exp for Var3

   1. Apply Adj PP Approach

   …

class rel

Ind Class 1 Rel = Ind Rate_{Class 1} / Ind Rate_Base

Assuming same VE & profit:

Ind Class 1 Rel = (PP_{Class 1} + FE per Exp_{Class 1}) / (PP_Base + FE per Exp_Base)

If no FE:

Ind Class 1 Rel = PP_{Class 1} / PP_Base

cats lr

Adjustments in Class Ratemaking

• Cat & Large Loss → replaced w/ loads

  • Consider whether some classes are more prone to _____

• One-Time Changes → need to on-level

  • esp for _____ Approach

• Credibility → important bc individual classes have less data

Ignored:

• Trends → assume all class trending at same rate

• Development → assume all class developing at same rate

• Expense & Profit → assume same variable loads for all classes

univariate

_____ Class Ratemaking

• Pros: simpler to explain, intuitive

• Cons: don’t properly account for exposure correlation

systematic noise diagnostics interactions response

Multivariate Classification (ex: GLMs)

• Accounts for exposure corr

• Attempts to focus on _____ effects in data & ignore _____

• Provides statistical _____ (ex: CIs)

• Considers _____ between rating vars → _____ correlation

minimum bias procedure

• a Multivariate classification

• Pro: corrects for exposure corr

• Cons:

  • Computationally inefficient (iterative)

  • Doesn’t test vars for statistical significance

link random software lr prem granular theoretical rates

Generalized Linear Models (GLMs)

• Corrects for exposure corr

• Select a dependent variable to run on → PP, Freq, Sev

  • Select _____ function & underlying _____ process

  • Use _____ to solve GLM and estimate relativities

• NOT typically run on _____ bc:

  • _____ needs to be on-levelled at _____ level

  • no common _____ distr for modeling LR

  • LR models become obsolete when _____ change

exponential normal constant

GLM vs Classical Linear Model

Response Variable

• GLM → member of _____ family of distributions

• Classical Lin Model → _____

Variance

• GLM → doesn’t have to be constant

• Classical Lin Model → _____

data anomalies ratemaking

Actuary’s Role in GLMs

• Obtaining reliable _____

• Exploring _____ w/ additional analysis

• Consider model results from statistical & business perspective

• Develop appropriate methods to communicate model results based on company’s _____ objectives

geo demographic weather property insured

External Data to use in GLMs

• _____-_____ info → pop density

• _____ → avg rainfall

• _____ characteristics → sq footage, quality of local fire dept

• Info ab _____ → credit scores

ded

GLM Outputs

**Check output makes sense

• Higher rates for higher _____ → doesn’t make sense

  • May be due to limited data at higher ded

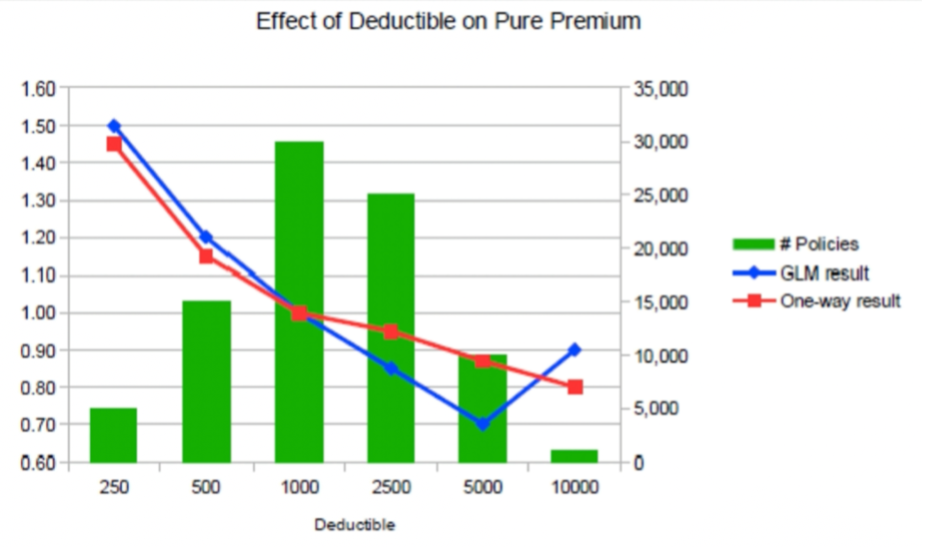
wide 1 same rel

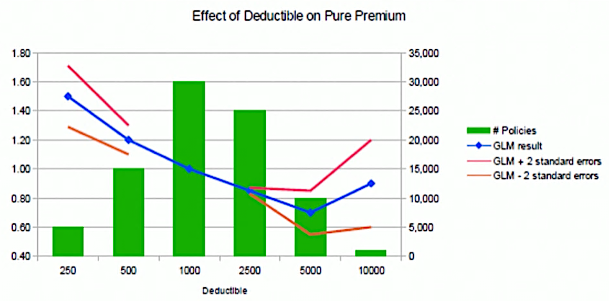
GLM Confidence Intervals

• Low volume of data → _____ CI

• Shows if each level & var as a whole is statistically significant

  • If CI includes _____ → no stat sig diff between that class & base

• Overlapping CIs → reasonable from statistical significance perspective to charge _____ _____

deviance tests

compares GLM models

Chi-Squared Test, F-statistic, AIC/BIC

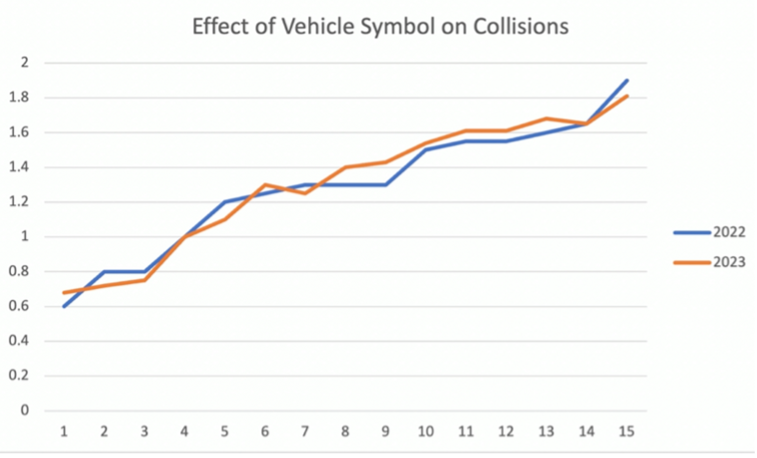
time consistency

tests whether GLM estimated parameters are consistent over time

• if diff years have similar patterns → model performing consistently

model validation overfitting underfitting

_____: measures model performance on unseen data

• compares prediction vs actual results

Reasons for not performing well:

• _____

• _____

factor cluster groups cart

Data Mining Techniques

_____ Analysis: reduce # of vars needed in GLMs

• Ex: using a single symbol var to capture multiple risk chars

_____ Analysis: combine similar risks into _____, resulting in fewer vars

• Ex: combining ZIPs into Territory variable

_____: build set of if-then rules to identify most important vars

• Detect interactions

• Classification & Regression Trees

territorial ratemaking

Challenges: highly correlated w/ other var → can use GLMs

• small geographic areas have low cred

Steps:

• Establish territorial boundaries

• Determine ind rates for each territory (using GLM)

spatial smoothing distance weather urban rural physical boundaries adjacency socio demographic

_____ _____: cred-weighting ind rates of neighbouring territories so no large discrepancies

• _____-based → better for _____

  • Assumes distance has same impact for _____ & _____ risks

  • Doesn’t consider _____ _____

• _____-based → better for _____ _____ perils (ex: theft)

  • Better reflects urban & rural differences

  • Considers physical boundaries

Over-smoothing: using geo units too far away, not relevant

Under-smoothing: giving local results too much cred → results too volatile

unit systematic residual spatial smoothing territories non contiguous

Establishing Territorial Boundaries:

• Define geographic _____ (ex: ZIP code, counties)

• Est geographic _____ risk for each unit → using GLMs

  • Unexplained geographic var incorporated into a _____ variable

• Apply _____ _____ on residual var

  • Smooth results across neighboring areas

• Cluster units into _____

  • Add constraints to avoid _____ _____ territories

ILFs less data impractical

Increased Limits Ratemaking

• Rated using _____ (Increased Limit Factors)

  • ILF = 1 → Basic Limit

• Can’t use standard ratemaking to price

  • ______ _____ for higher amts → volatile

  • _____ results → ex: higher price for higher limit

Importance:

• Ppl need more covg as wealth grows

• Trends have more impact on increased lim than basic lim

• More lawsuits, higher jury awards

ILF trend develop layer variable same freq indep

Standard _____ Approach

• _____ & _____ data first!

  • bc they may vary by _____

• Assumptions:

  • All UW expenses & profit are _____ and _____ for all lims

  • _____ same for all lims

  • Freq & sev _____

expense profits freq

ILF(H) = Rate_H / Rate_B

= (PP incl LAE_H / 1-V_H-Q_H) / (PP incl LAE_B / 1-V_B-Q_B)

= PP incl LAE_H / PP incl LAE_B → same UW _____ & _____

= (Freq_H x Sev_H) / (Freq_B x Sev_B)

= Sev_H / Sev_B → same _____

=LAS(H) / LAS(B)

full losses claims

Limited Avg Severity (LAS):

• For loss < H → _____ loss amt

• For loss > H → # of claims x H

LAS(H) = _____ capped at H / # of _____

x-h k

LAS for layer K xs H:

• Below H → don’t contribute

• Between [H, H+K] → contribute only what’s above H, i.e. _____

• Above H+K → contribute full _____

• Denominator → Only include losses that contributed to num

  • i.e. exclude claims below H

LAS(K xs H) = Losses in layer / # Claims contributing to layer

lower

LAS for Censored Data

• Lowest limit → same as uncensored

• Higher limit → calculate incrementally

LAS(H₂) = LAS(H₁) + LAS(layer between H₁, H₂) x Pr(X > H₁)

• Can’t use data from _____ limits bc don’t know uncapped loss!

• Pr(X > H₁) → Only based on policies that could have claim above H₁

  • exclude claims capped at lower lims

deductible pricing

2 Types of Deductibles:

• Flat dollar

• Percentage

**Trend & develop data first!

expenses profits variable xs ratio ler

Ded Pricing: Loss Elimination Ratio (LER) Approach

• Assumes all UW _____ & _____ are _____

• Base = no ded → Ind Rel = 1

Ind Rel(D) = _____ _____(D)

= Loss&LAE above D / Ground-up Loss&LAE

= 1 - Loss&LAE below D / Ground-up Loss&LAE

= 1 - ____(D)

**Denom is ALL ground-up loss (not basic loss!)

ler behaviour incentive

_____ Approach to ded pricing assumes claimant ______ will NOT vary by ded

• GLM & Univariate Analysis → can vary!

• Ex: financial _____ in filing a $501 claim w/ $100 ded vs $500 ded

1 - ler(d w/ base b)

LER for censored data

• Don’t know claims below ded

• Can only use claims where amt at BOTH ded are known!

LER(D w/ base B) = Diff in Loss assuming diff deds / Loss assuming B ded

Ind Rel(D) = ______

dollar caps coverage percentage

Deductible impact on Premium

• Higher ded = lower prem

• Problem if increasing ded lowers prem more than ded difference

Limit prem impact by:

• _____ _____ on prem credit for ded

• Vary ded factors by _____ amount

• _____ ded

lower censored

Problems w/ Deductible or Limit data to price ded:

• Policies w/ ded may only have data for loss xs of ded

  • Sol’n:

    • GLM

    • LER approach using only data from ded _____ than ded you’re pricing

• Policies w/ lim may only have data for loss _____ by historical lim

  • Sol’n: GLM

dec undercharged overcharged expense constant fe size writing prem discount larger

Work Comp Size of Risk

• FE as % of prem should _____ as prem inc

• So small risks are not _____, large risks not _____

_____: accounts for ____ that don’t vary by _____ of risk

• so small risks not undercharged

• prem might not be enough to cover FE of _____ the policy

_____: % discount for _____ policies

• so large risks not overcharged

• to recognize that expenses are a lower % of prem than small risks

lowest expense reduction portion

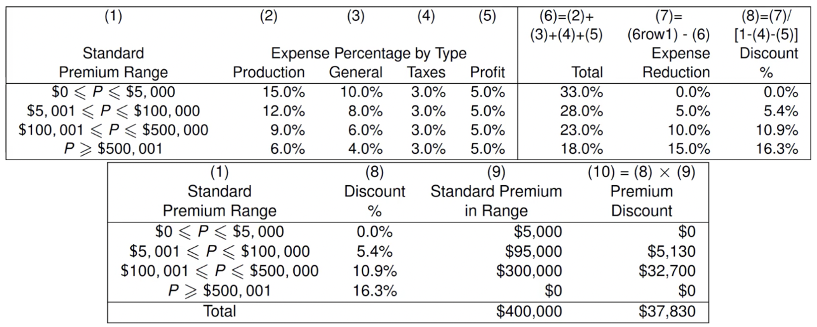
Premium Discount

• Sum expenses for each range of loss

• Expense Reduction = diff w/ expense of _____ range

• Discount % = _____ _____ / (1 - VE)

  • VE % are same for all claim sizes → Taxes, Profit

• Std Prem in Range = _____ of std prem in each range

  • Start w/ smallest range until it adds up to full amt of std prem

• Prem Discount = Std Prem in Range x Discount %

safety return injured experience rating prevent loss constants

Small Work Comp insureds have worse loss experience bc

• Have less sophisticated _____ programs

• Don’t have _____ to work programs for _____ workers

• Not as impacted / don’t qualify for _____ _____

  • Less incentive to _____ injuries

• Price for this diff using GLMs or _____ _____

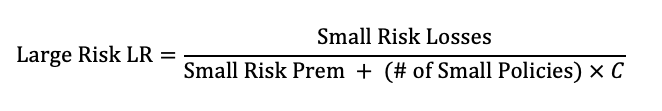
expected loss experience equalizes

Loss Constants: accounts for fact that small risks have worse _____ _____ _____ than large risks

• _____ LR between small & large risks

• Added to prem of either 1) small risks only; or 2) both risks

Steps:

• Equate LR of small & large risk

  • Add C x # of policies to prem in Denom

• Solve for C

covg amt replacement cost

Insurance to Value (ITV)

• For Homeowners or Commercial Property insurance

• Coverage Amt = Face Amt

ITV = _____ / _____

underinsured inc dec

_____: when ITV < 100% → i.e. covg < replacement

• Ind Rate per $1k covg _____ as ITV _____ (if partial loss possible)

fully covered rates inadequate vary coinsurance

Issues when Underinsured:

• Insured not _____ _____ in event of total or near-total loss

• If insurer assumes 100% ITV in _____, prem will be _____

Sol’ns:

• _____ rates by ITV

• _____

covg amt

ITV:

Ind Rate = PP = Freq x Sev

Ind Rate per $100k covg = PP / (_____ _____/100)

higher undercharged

Underinsured will pay _____ rate per $1k covg

• So if charging all at same rate, underinsured will be _____

adequate equitable

_____: prem ≥ expected policy costs (loss + expenses)

_____: prem relatively fair across insureds

• Equal LR for all risks

• should not be subsidizing

*Compare prem to expected costs

sev dec constant inc

ITV → _____ Distribution

• As ITV dec, ind rate per $1k covg inc

• As ITV inc, ind rate per $1k covg dec!

  • Rate depends on sev distr!

As covg inc, ind rate per $1k covg will DECREASE at…

Right-skewed (small loss likely) → _____ rate

Uniform → _____

Left-skewed (large loss likely) → _____ rate

tools home characteristics inspections

Guaranteed Replacement Cost (GRC)

• If home insured at 100% ITV, total loss guaranteed will be covered regardless of actual cost

• Past: hard to est Replacement Cost

• NOW:

  • Better _____ to estimate RC based on _____ _____

  • Property _____ → get more accurate info for est

coinsurance underinsurance penalty

_____: insured also responsible for a portion of loss

• Another sol’n to _____

  • Instead of inc rates, insurer reduce loss!

• Implemented by coinsurance clause

• Coinsurance requirement = X% ITV

  • If ITV < X% → coinsurance _____ apply

proportional underinsurance penalty PP underinsured

Coinsurance & EQUITABLE rates:

• Adjust amt insurers pay on claims _____ to amt of _____

• After coinsurance _____ applied, all risks will have equal _____ per $1k covg

  • Makes single rate per $1k covg for all ITV levels is equitable

Coinsurance & ADEQUACY:

• Reduce paid loss on _____ risks s.t. the same rate as risks insured to coinsurance requirement will be adequate

replacement covg loss

COINSURANCE

Coinsurance Apportionment Ratio:

a = min(1, Covg / (Coins Req% x _____ Cost))

Indemnity before ded: I = min( a x Loss , _____)

• Indemnity after ded: I - ded

Coinsurance Penalty = min(_____, Covg) - I

less loss

Coinsurance Penalty will be positive if 2 conditions:

1. Insured for _____ than coinsurance req

2. _____ occurs that’s less than coinsurance req

covg coinsurance requirement

Coinsurance Penalty Graph

• Max penalty @ loss = _____

• Dec to 0 @ loss = _____ _____

credibility

when historical data is volatile or small in volume → may not be fully reliable

give some weight to other related experience to improve ests

decreasing

3 Criteria for Credibility:

1. 0 ≤ Z ≤ 1

2. As n inc, Z inc → dZ/dn ≥ 0

3. As n inc, Z inc at _____ rate → d/dn (Z/n) < 0

evpv/vhm

Buhlmannn (Least Squares) Credibility

k = _____

Z = n / (n+k)

accurate unbiased indep available compute logical

5 Desirable Qualities for a Cred Complement

1. _____

   • Stable, low var, large volume

2. _____

   • Adjust for diff between states / another company’s book of business

3. Statistically _____ from base stat

   • Subject isn’t large portion of complement

4. _____

5. Easy to _____

   • Ex: use same methods used to produce small insurer ind on large insurer data

6. ______ relationship to base stat

   • Ex: both insurers write personal auto in same state

larger group related rate change present harwayne trended competitor

Complements in First Dollar Ratemaking

1. LC of _____ _____ that includes group being rated

2. LC of larger _____ group

3. _____ _____ from larger group applied to _____ rates

4. _____’s Method

5. _____ Present Rates

6. _____’s Rates

accurate available compute logical biased

Complement: LC of Larger Group that includes group being rated

• Pro: _____, _____, easy to _____, _____

  • Indep if subject experience excluded

• Con: _____ bc there’s reason why subject is separated from larger group

indep available compute biased

Complement: LC of Larger Related Group

• Pro: _____, _____, easy to _____

  • Possibly accurate, logical relationship

• Con: _____

biased

Complement: Rate Chg from Larger Group applied to Present Rates

• Adj ver of LC of Larger Grp → less _____

• Pro: easy to compute

C = Current LC_Subject x (Ind LC_Larger / Current Avg LC_Larger)

accurate unbiased available logical compute exposures adj factor

Complement: Harwayne’s Method

• Adjusts for overall LC diff between states, exposure distr differences

• Pro: _____, _____, mostly indep, _____, _____ relationship

• Con: hard to _____

EX: Want complement for State A Class 1 LC

• Calculated Wtd-Avg PP for State A

• Calculate Wtd-Avg PP for other states using State A’s _____

• _____ _____ = Wtd-Avg PP_{State A} / Wtd-Avg PP_{other state}

• For each other state: Adj Class 1 LC = Class 1 LC x Adj Factor

  • C = wtd avg of all Adj Class 1 LC using Class 1 exposures

residual unbiased available compute logical inaccurate ind implemented

Complement: Trended Present Rates

• Adjust current rates for trends & _____ indication

• Pro: _____, _____, easy to _____, _____ relationship

• Con: may be _____ if ind volatile, may or may not be indep

Trend Period:

• From OG target effective date of last review (NOT actual implementation date)

• To: target effective date of next rate chg

PP Method:

C = Trended Curr Rate x (Prior _____ LC / Prior _____ LC)

LR Method:

• Note: LR Trend = Loss Trend / Prem Trend

C = LR Trend Factor x (Prior Ind Rate Chg Factor/Prior Imp Rate Chg Factor) - 1

k p

Classical Cred:

• Observed is within _____ of its expected mean w/ prob = _____

# claims for full cred = (z_(p+1)/2 / k)²

indep loss distr accurate biased expected lr compute

Complements in XS Ratemaking

• Complement for layer L xs of A → (A, A+L)

1. Inc Limits Analysis

   • Use ground-up loss up to attachment pt A

   • Pro: _____

   • Con: biased if ILFs based on a diff _____ _____, inaccurate due to low volume of data

2. Lower Limits Analysis

   • Use data capped at lower lim d

   • Pro: more _____ than inc lim

   • Con: more _____

3. Limits Analysis

   • Use data capped at all limits greater than A

   • Pro: for reinsurers that don’t have ground-up data

   • Con: biased, inaccurate, assumes same _____ _____ for all limits

4. Fitted Curves

   • Pro: accurate, less biased, logical relationship

   • Con: less indep, hard to _____, data may not be available

inc lim analysis

lower lim analysis

limits analysis

For all limits d > A