I hate math

Derivatives of all trig functions

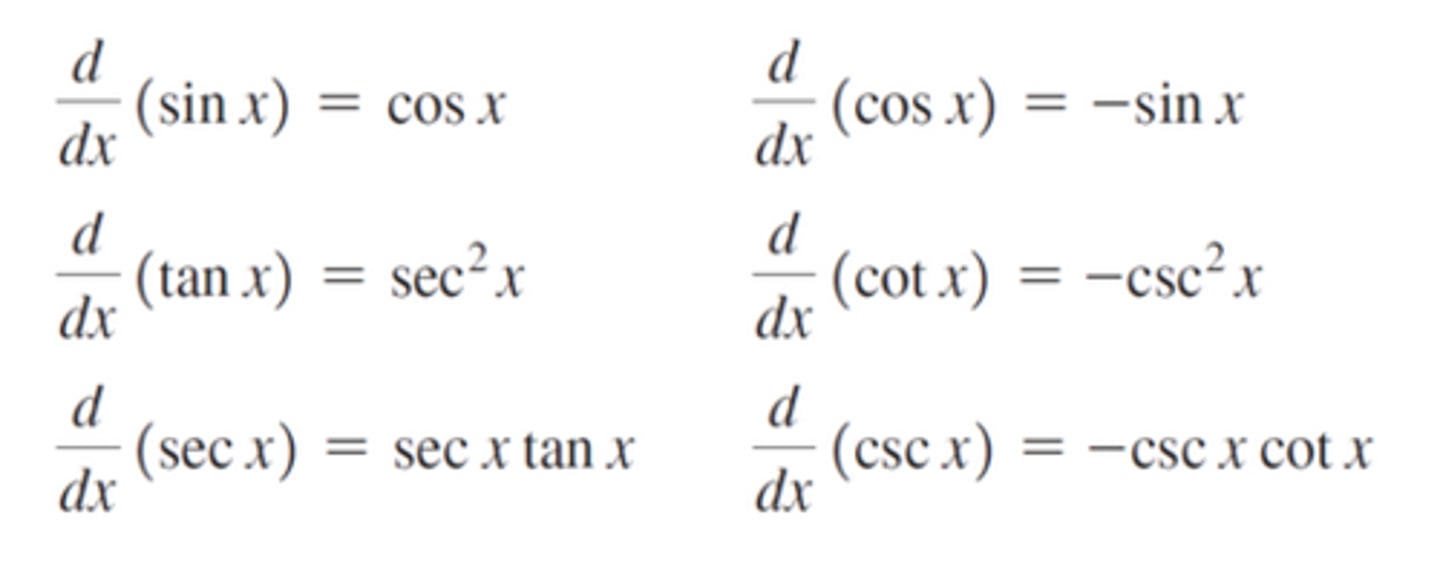
Derivative of all inverse trig functions

make sure sec & csc have absolute value x outside of the radical

derivative of double angle

integral of double angle

derivative of sin2x = 2cos2x

integral of sin2x = -1/2cos2x

integral of sec

if its 2x, for example, put 1/2 at the beginning

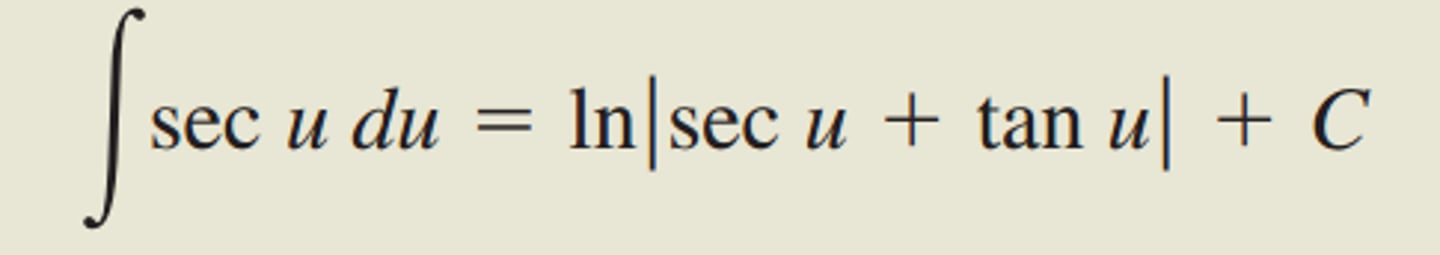
Integral of csc

ln |csc - cot|

if its 2x, for example, put 1/2 at the beginning

integral of tan

if its 2x, for example, put 1/2 at the beginning

-ln|cosx| + C

ln|secx|

integral of cot

if its 2x, for example, put 1/2 at the beginning

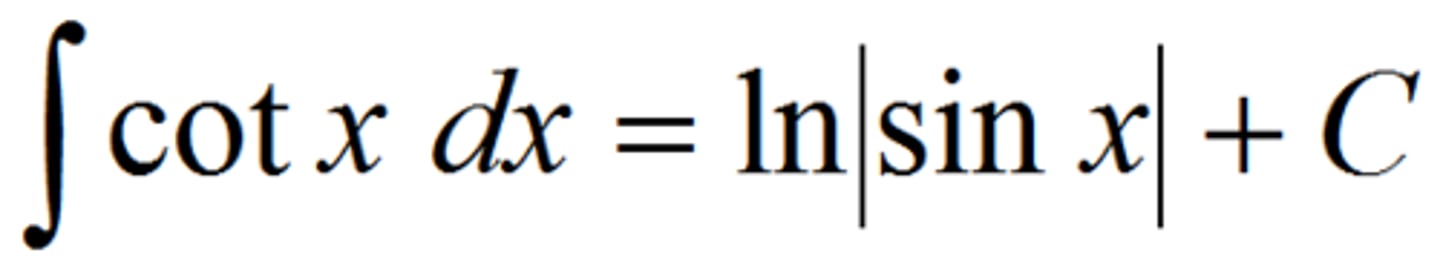
that one Sin inverse identity

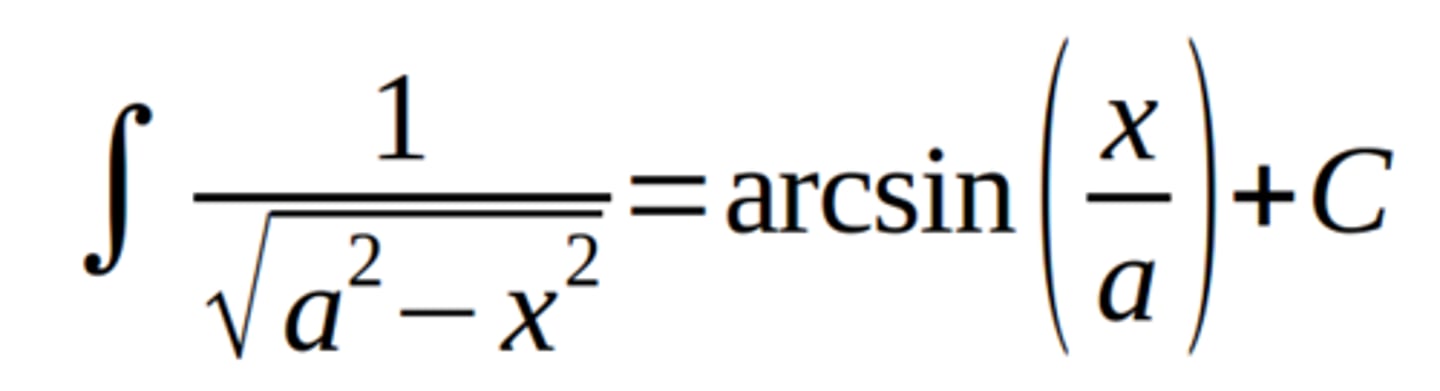
that one tan inverse identity

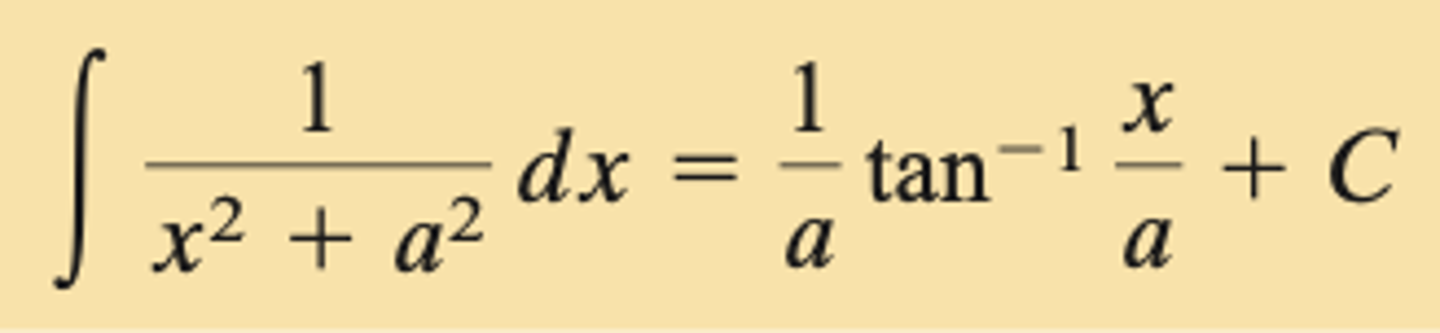
integrating sinx ^n or cosx ^n when n = odd

Bc odd, split a sin² or cos² into the identity sin² + cos² = 1

Keep one sin or cos for u-sub

The reason why we split it is bc u-sub needs a function & its derivative next to each other

integrating sin^n or cos^n when n = even

Use half-angle formulas

Sin half angle is the same except its sin² = 1 - cos2x /2

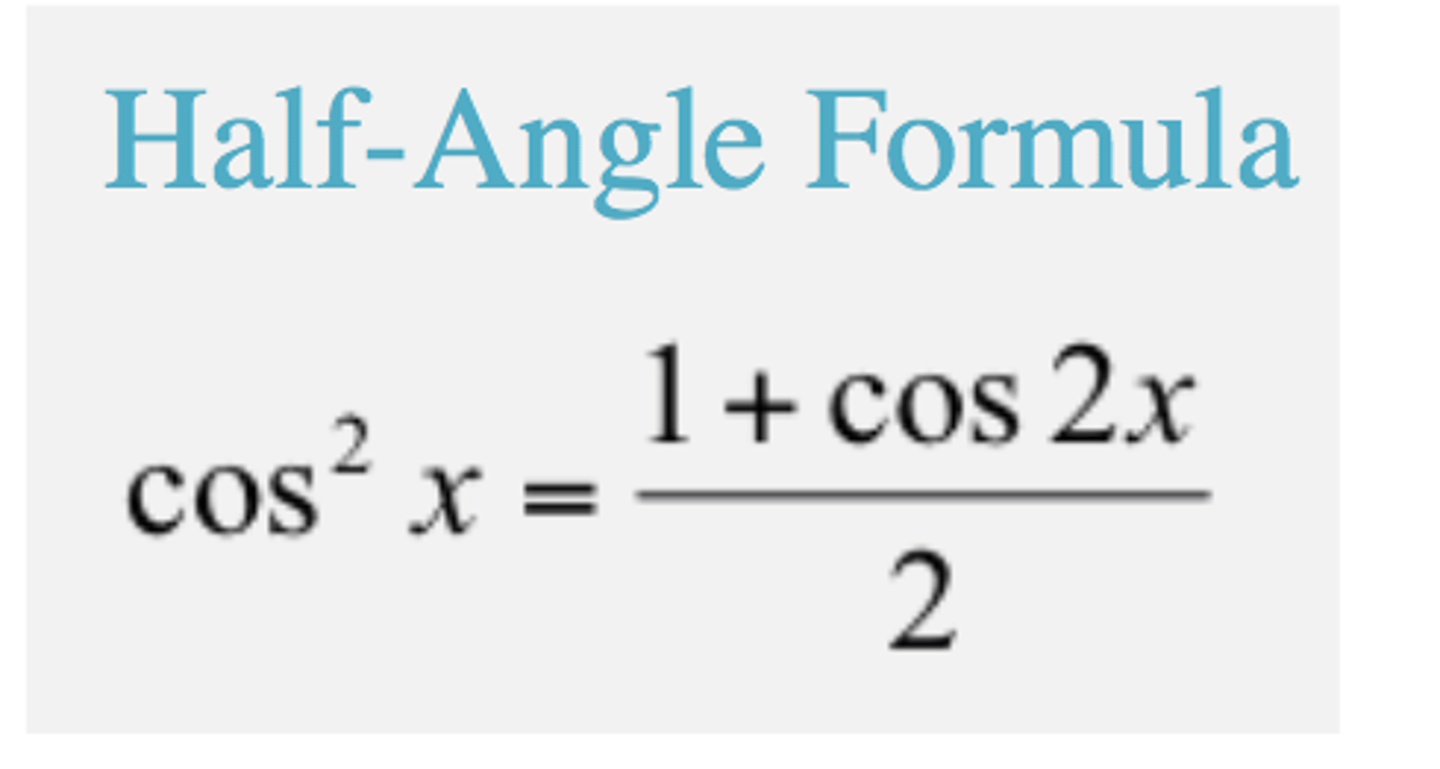
sin^m(x)cos^n(x) m or n is odd

From odd power, keep one sinx or cosx for u-sub

Use identities to substitute

sin^n(x)cos^m(x) n &m = even

Use half angle identities again

Sin half angle is the same except its sin² = 1 - cos2x /2

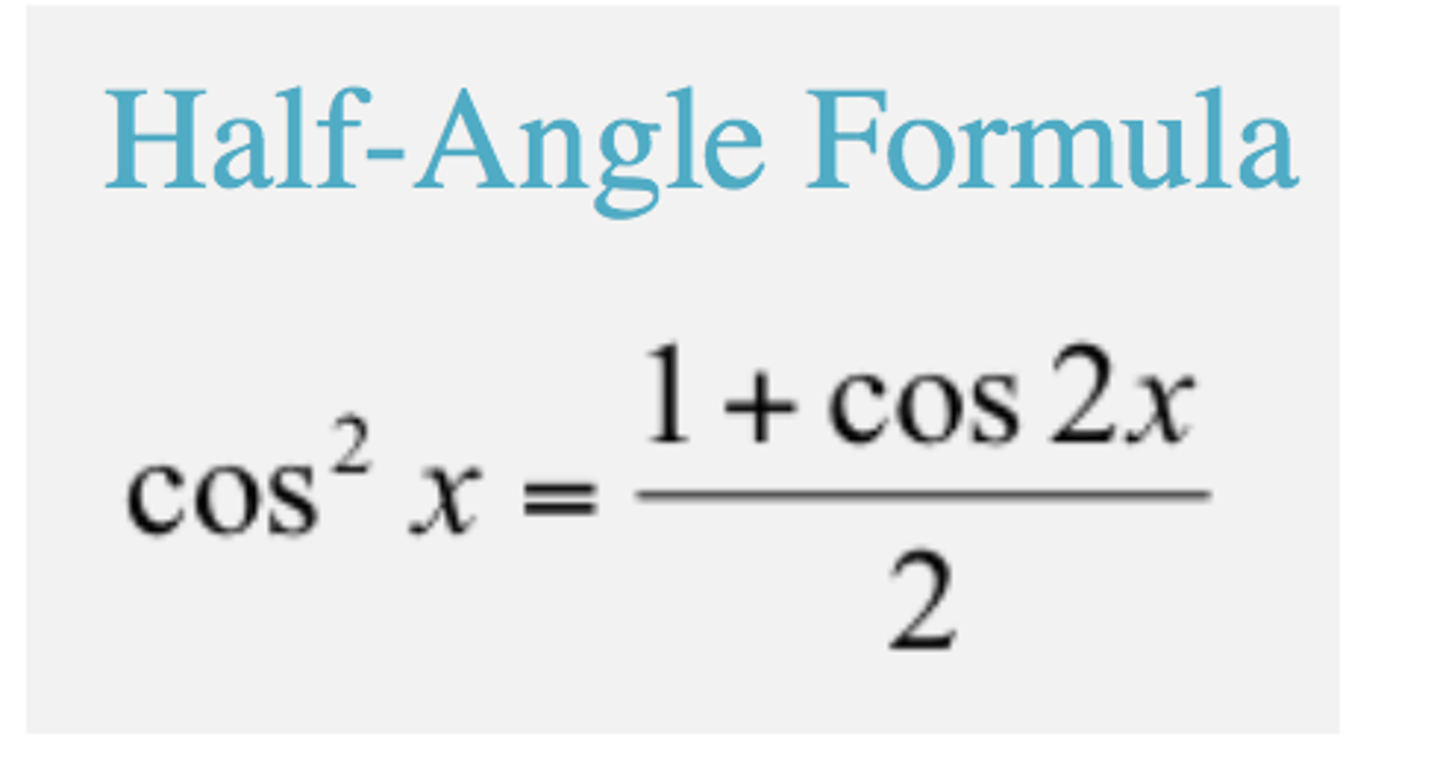
tan^n or cot^m

From power full out tan² or cot² and substitute cot² = csc² - 1 or tan² = sec² - 1

tan^m(x)sec^n(x) or cot^m(x)csc^n(x) where n = even

Pull out sec² or csc² for u-sub

integration by parts

integral of x^-1

DONT FORGET THE ABSOLUTE VALUE

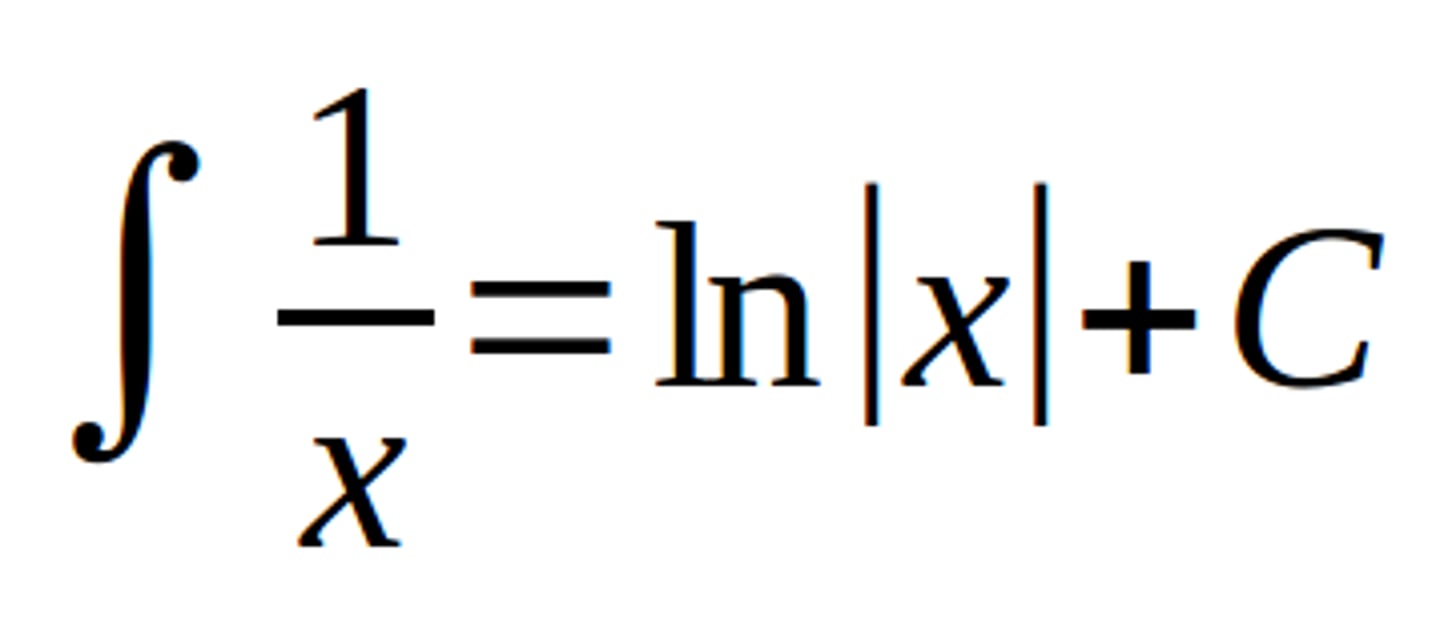
how to do distance

find the zeroes of position (setting position derivative = 0 and finding the x values) then do the integral between each zero. for negative numbers, put a negative in front of them to make them positive bc distance is ALWAYS POSITIVE

integral of exponential

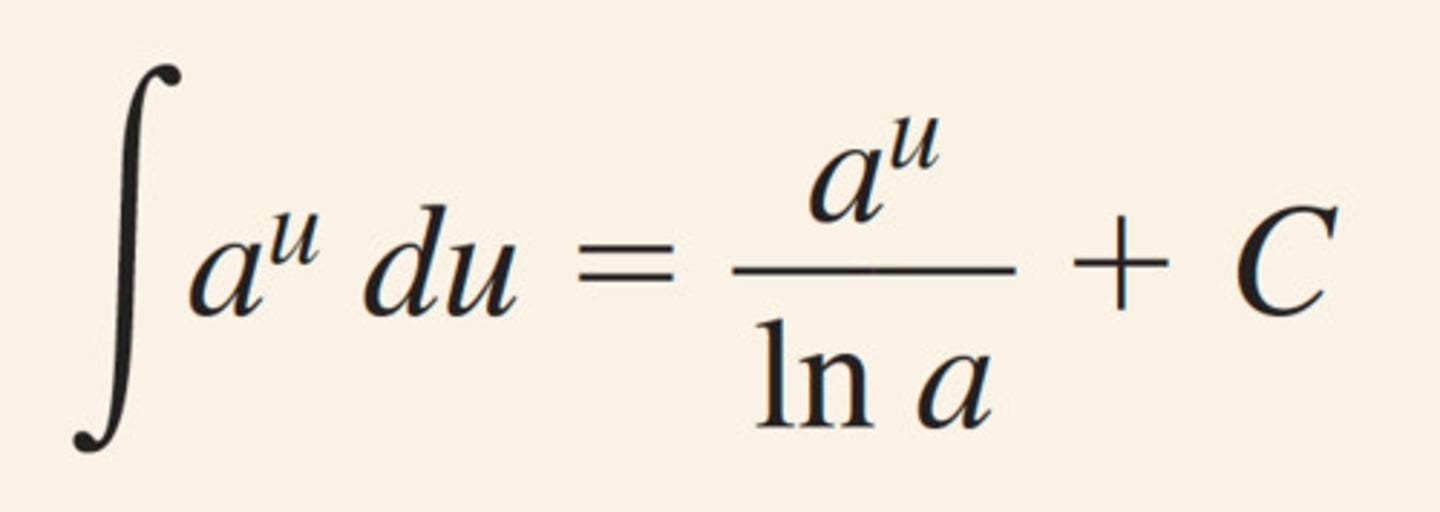
Total Change Theorem

the integral of a rate of change is the total change

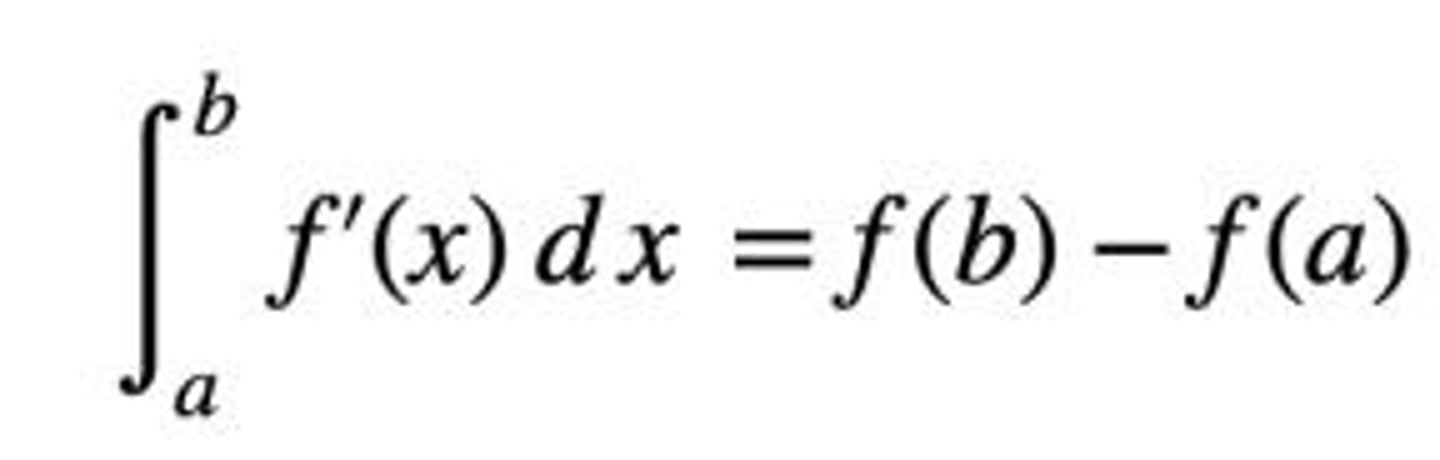
average value theorem

the c value you get is the y value. put this in for y, and solve for x in the original equation

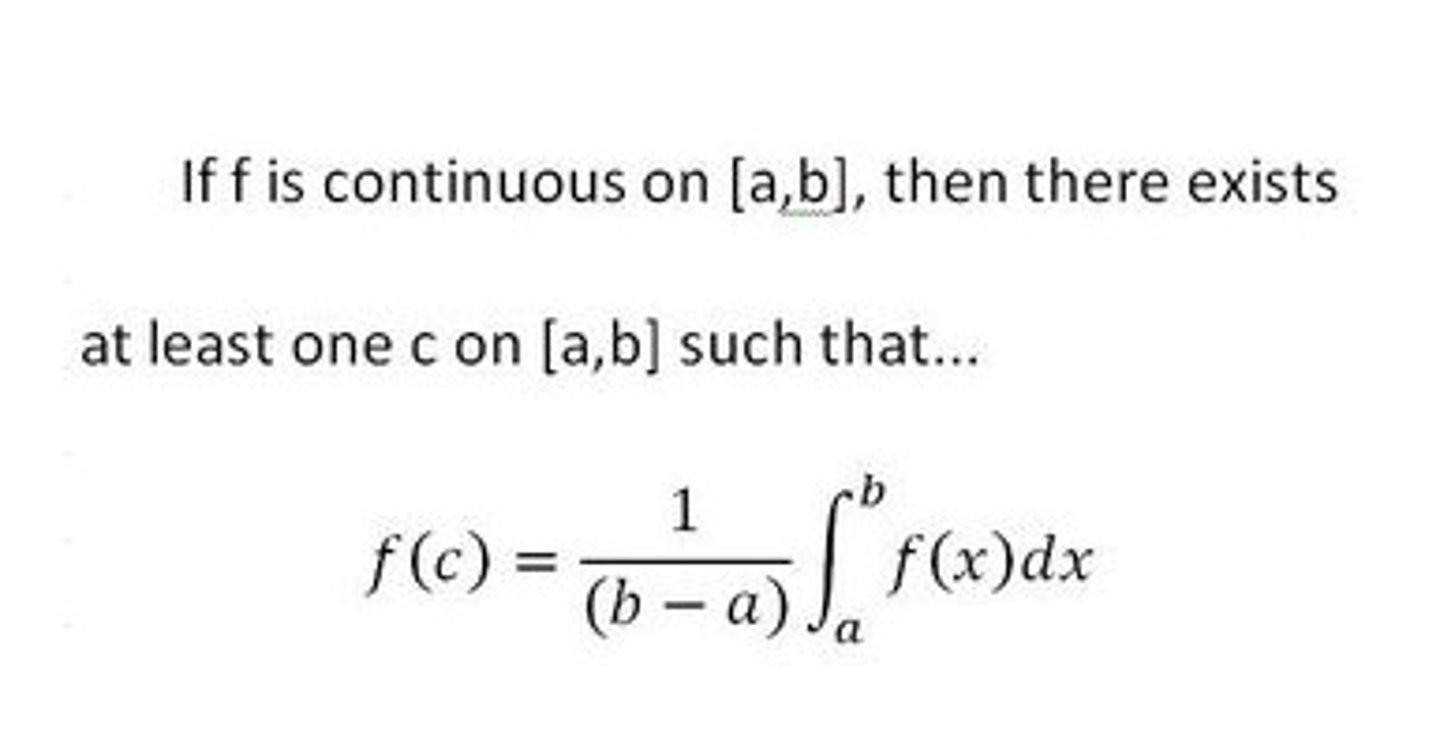
definite integral of a derivative

the total change in the original equation:

ex: definite integral of velocity = displacement of position (change in x)

you can combine terms after integrating before doing upper bound - lower bound

ok

integral of lnx

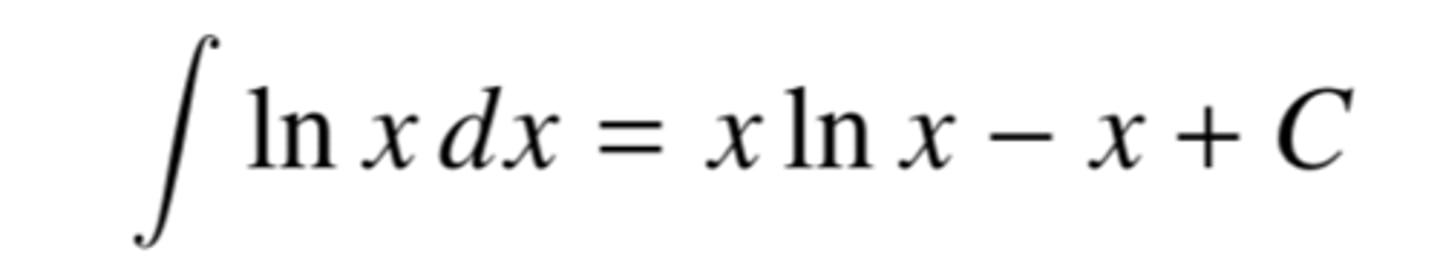
cos2x

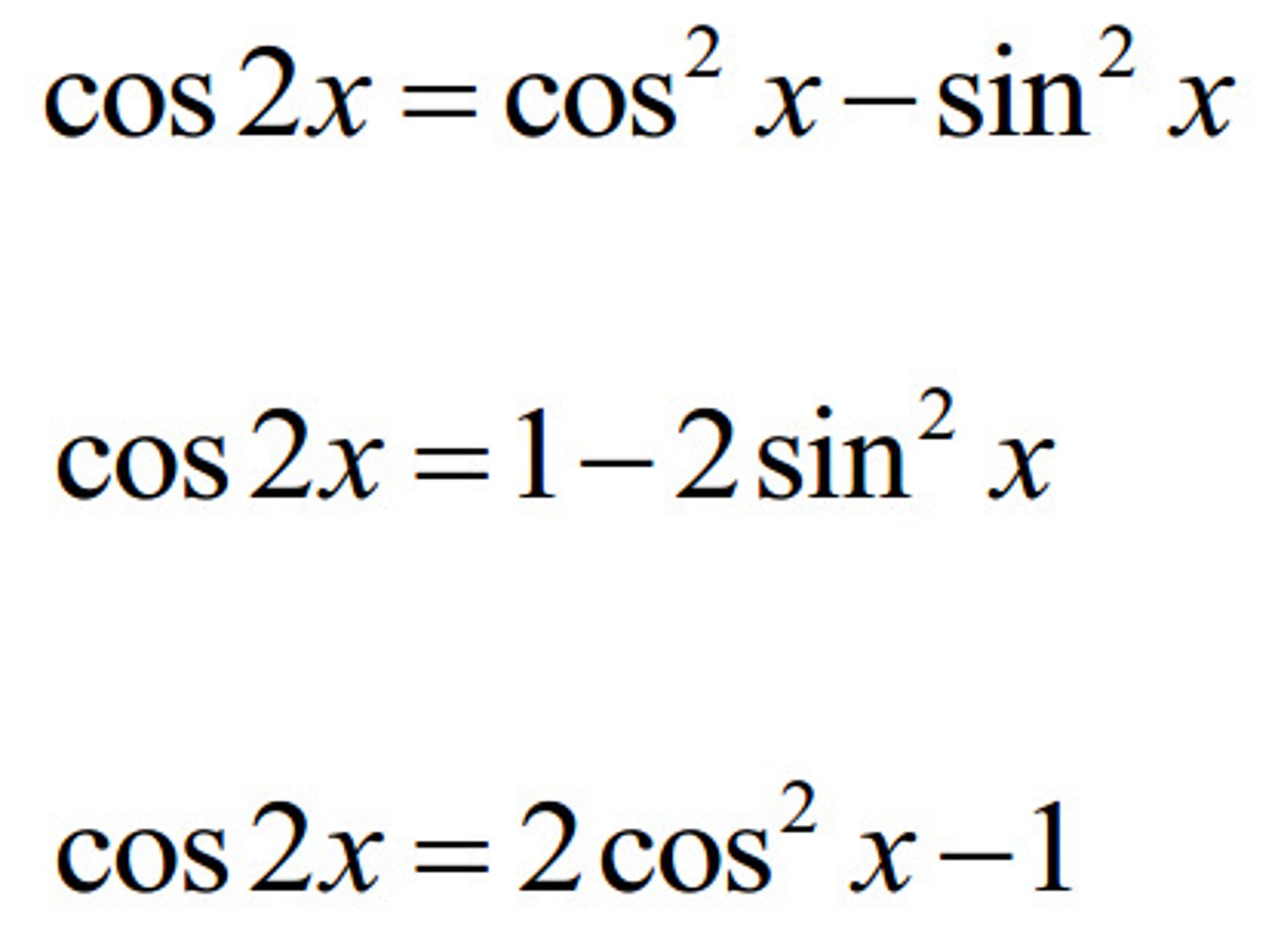
completing the square

DONT