z-Score and Normal Distribution

Normal Distributions

• This is the most important and widely used distribution - Bell Curve

Normal Distributions Characteristics

• Normal distributions are symmetric around their mean

• The mean, median, and mode of a normal distribution are equal (all with each other)

• The area under the normal curve is equal to 1

• Normal distribution is denser in the center (middle highest point/more scores) and less dense in the tails (less scores)

• Issues with Raw Scores

• Required to calculate mean alongside SD of the distribution for interpretation

• Can’t tell if score is good or bad by itself (don’t know where the score stands or how to interpret it) - no frame of reference

z-Scores will resolve this issue by showing us how far or close raw scores are from the mean (tells us how far that score is from the average)

mean = average score

z-Scores

We transform our X values into Z-Scores to tell us how far away score is from mean (in units of the standard deviation and + or - direction)

• will show us exactly where our raw scores is located within it’s distribution

• can compare Z-Scores to other Z-scores in different distributions

z-Scores Distribution Properties

• Mean of z-Score distribution is always 0

• The standard deviation of the z-Score is always 1

• The shape is always the. same as the original distribution

Interpreting z-Scores

• Sign tells us whether the score is above (+) or below (-) the mean

• Number tells us the distance between the score and the mean

z-Score Formula

1. take your X-Value (X) and subtract by your Mean Population (μ)

2. Then divide by your Population Standard Deviation (σ)

3. You now calculated your z-Score!

z-Score to Raw Score (X)

1. Take your Population Mean and add to your calculated/multiplied z-Score and Population SD

2. Once you calculated that all together, you have your z-Score to Raw Score

Sample z-Score

Same as population, just different symbols (this is to get z-Score value, so X-Value subtracted by your Mean, then divided by your Sample SD)

Putting it all together: Standardized Distribution Problem

Find your z-Score, then transform z-Score to raw score

• answer is found!

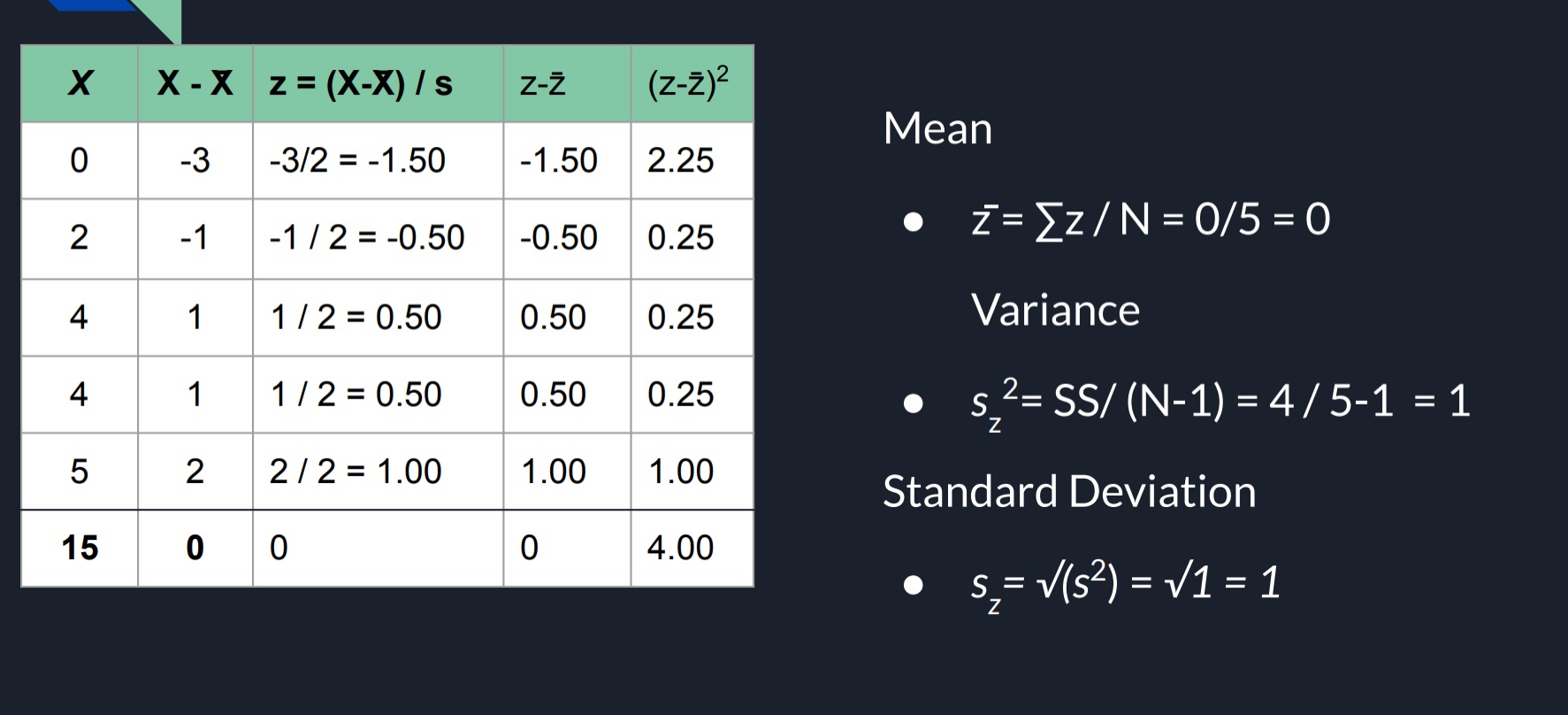
z-Score mean (z̄)

z̄ = ∑z/N

• Average z-Score of distribution

• remember z-Score mean properties state it’ll always equal (z̄ = 0)

Squared Deviation (SS) AND Sum of Squares (SS)

(z - z̄)² - Squared Deviation (IN GENERAL SENSE)

• power by 2 your calculated z-Score subtracted by your z-Score mean

- btw, because z̄ is 0, you’ll just be powering your z-Score

Σ(z - z̄)² - Sum of Squares (IN GENERAL SENSE

Sample z-Score Variance (S_z²)

1. find your Squared Deviation (SS)

2. divide by n-1

3. YOU’LL ALWAYS GET THE ANSWER 1; z-Score properties state z-Score Variance will always equal 1 (S_z² = 1)

NOTE: when you do anything with a z-Score, you’ll need to have already solved your OG Population and Sample Standard Deviation. You literally need that JUST to get your z-Score. Everything is new after that!

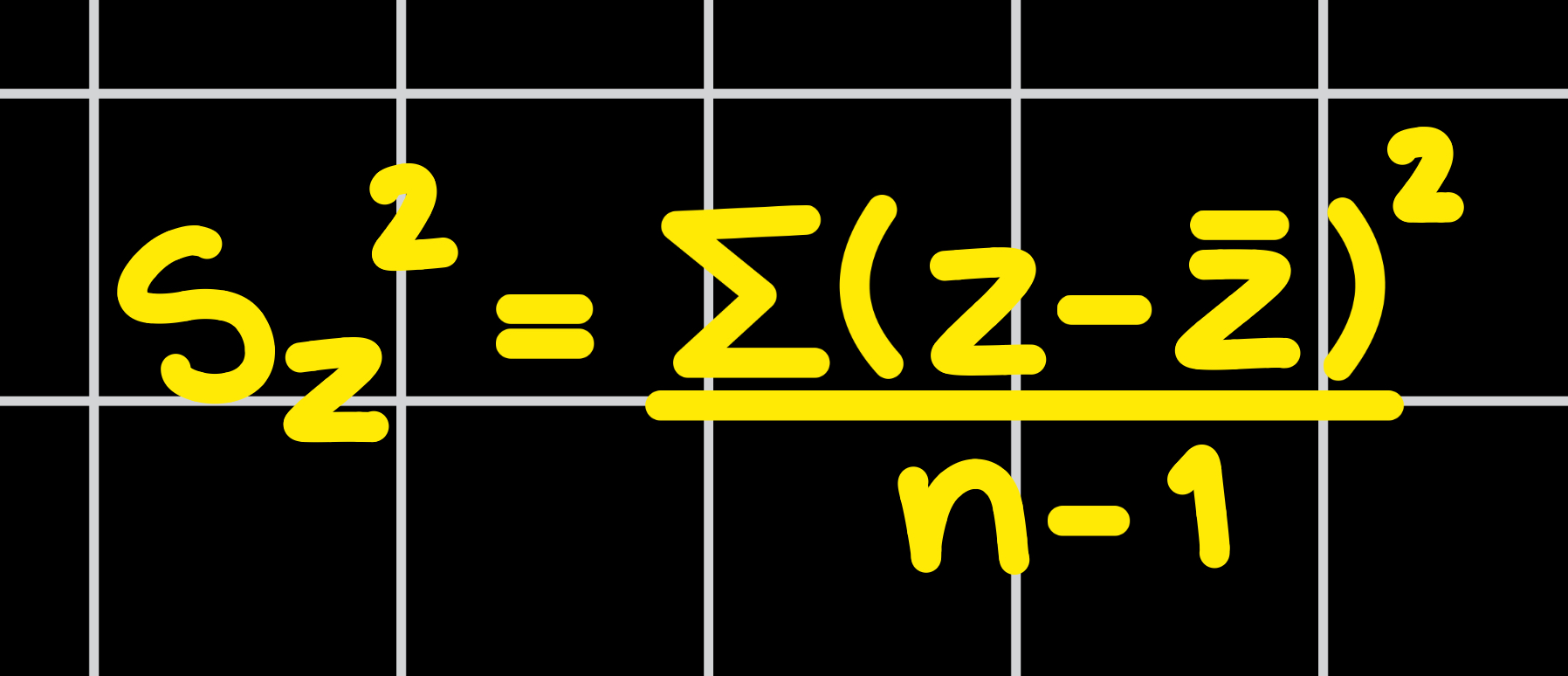
Sample z-Score Standard Devation

1. square your Sample z-Score Variance

1. YOU’LL ALWAYS GET THE ANSWER 1; z-Score properties state z-Score Standard Deviation will always equal 1 (S_z = 1)

NOTE: when you do anything with a z-Score, you’ll need to have already solved your OG Population and Sample Standard Deviation. You literally need that JUST to get your z-Score. Everything is new after that!

Putting it all together: Standardized Distribution Table

1. Find your z-Score

2. Find your z-Score mean (z̄ = 0)

3. Find your Sample z-Score Variance (S_z² = 1)

4. Find your Sample z-Score Standard Deviation (S_z = 1)