Edexcel A Level Maths- Paper 1

integrate sinx

-cosx + c

integrate cosx

sinx + c

integrate sec^2 x

tanx + c

integrate cosecxcotx

-cosecx + c

integrate cosec^2x

-cotx + c

integrate secxtanx

secx + c

cot^2 x

cosec^2 x- 1

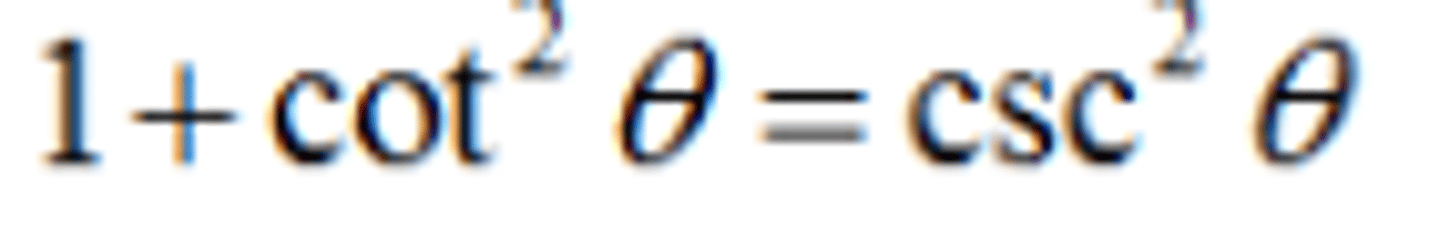
tan^2 x

sec^2 x - 1

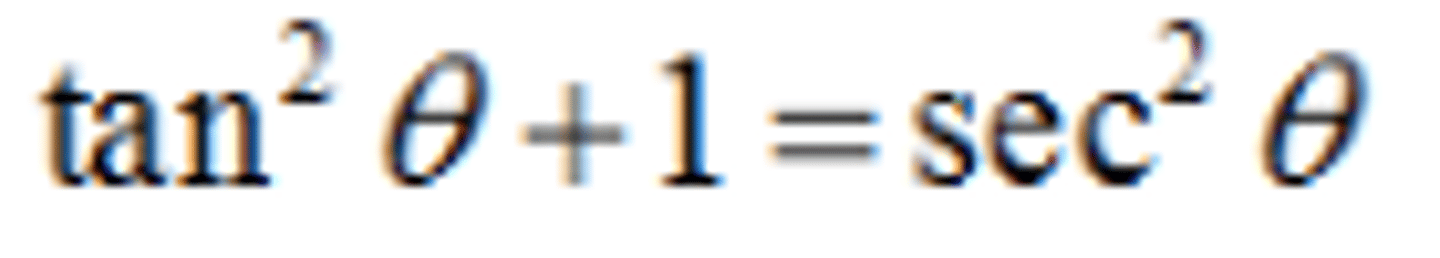
sin^2 x

1 - cos^2 x

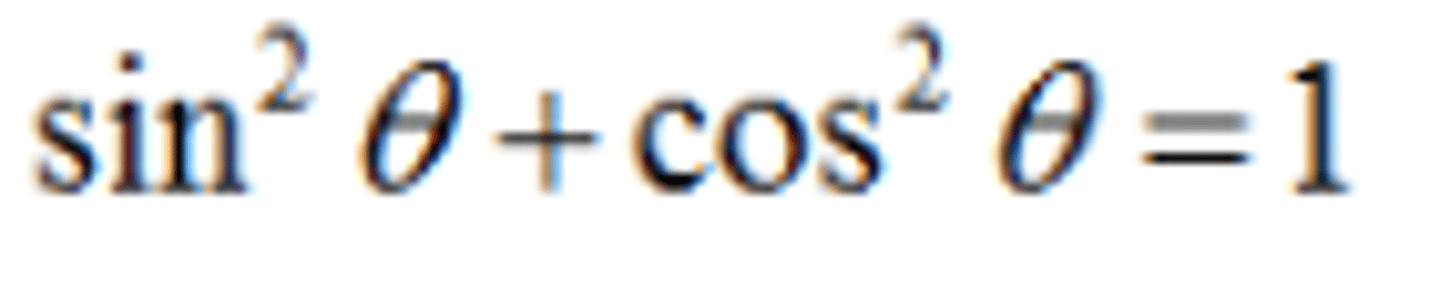
sin^2 x

1-cos2x/2

cos^2 x

1+cos2x/2

1/x

ln IxI + C

Differentiate sin x

cos x

Differentiate tan x

sec² x

Differentiate cot x

- cosec² x

Differentiate sec x

sec x tan x

Differentiate cos x

- sin x

Differentiate cosec x

- cosec x cot x

Differentiate sin 2x

2 cos 2x

Differentiate cot 3x

- 3 cosec² 3x

Differentiate sin² x

2 sin x cos x

Differentiate cos 0.5x

- 0.5 sin 0.5x

Differentiate sin x cos x

cos 2x

Differentiate 2cos0.5x

-sin0.5x

1 + tan2θ

= sec2θ

cot2θ + 1 = cosec2θ

= cosec2θ

Sin2θ

2sinθcosθ

Cos2θ

cos²θ-sin²θ
2cos²θ-1
1-2sin²θ

Tan2θ

2tanθ / (1 - tan²θ)

How do you write a rational number in a proof?

a/b

What does y=|f(x)| do?

Reflects values below the x-axis in the x-axis

What does y=f(|x|) do?

Reflects values of x≥0 in the y-axis

Arithmetic sequence formula

a₁+(n-1)d

Geometric sequence formula

uₙ = arⁿ⁻¹

Convergent geometric series

Convergent if |r|<1 where r is the common ratio

Periodic sequences

Sequence is periodic if terms repeat in a cycle

Vectors and angles

If the vector a = xi + yj + zk makes an angle θₓ with the positive x-axis, then cos(θₓ) = x/(|a|) and similarly for the angles θᵧ and θz.

Radian to degree conversion

1 radian = 180°= π

Arc length

l=rθ

Area of a circle sector

a=1/2 x r²θ

Arcsin(x) Graph

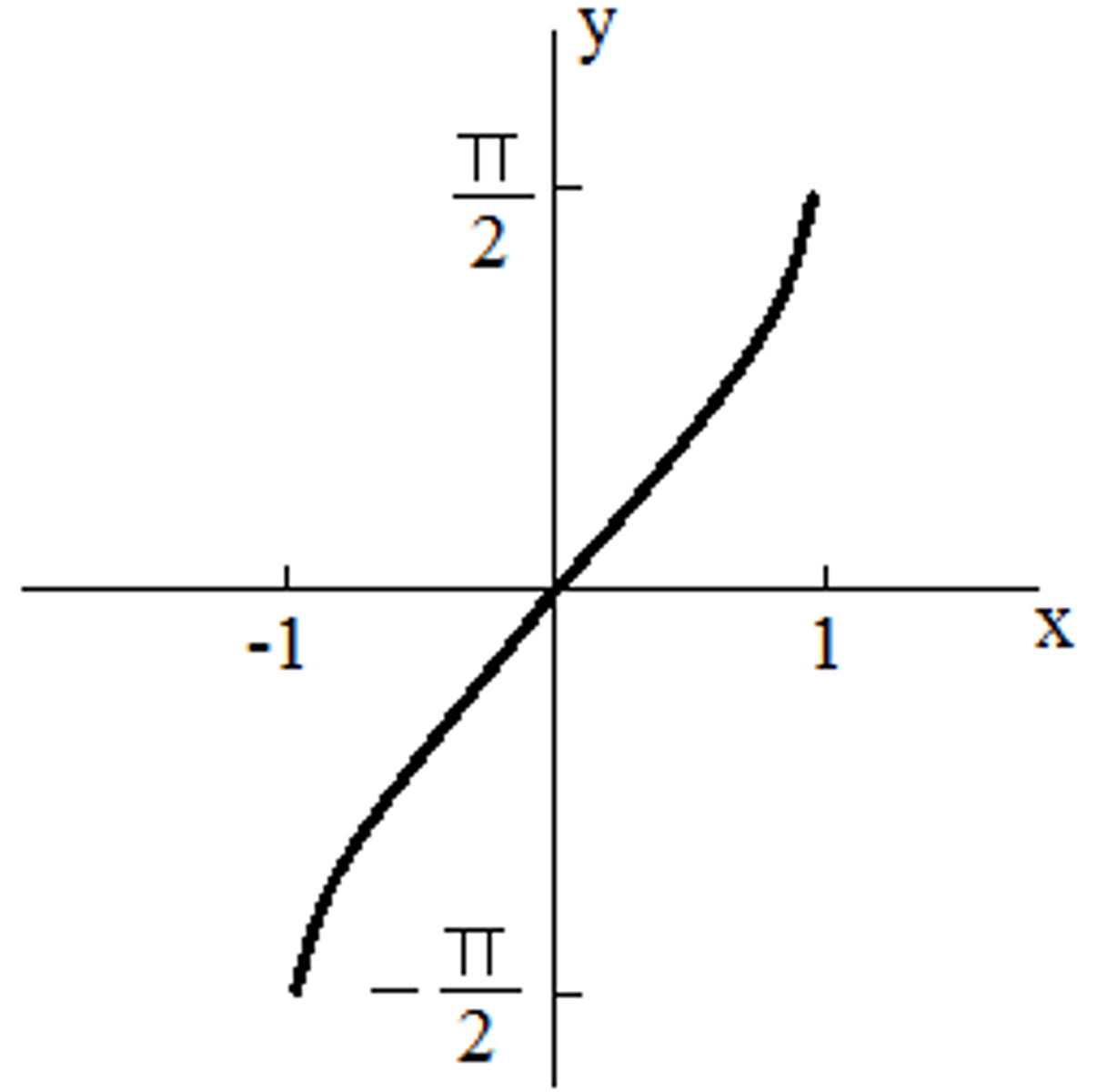
Arccos(x) Graph

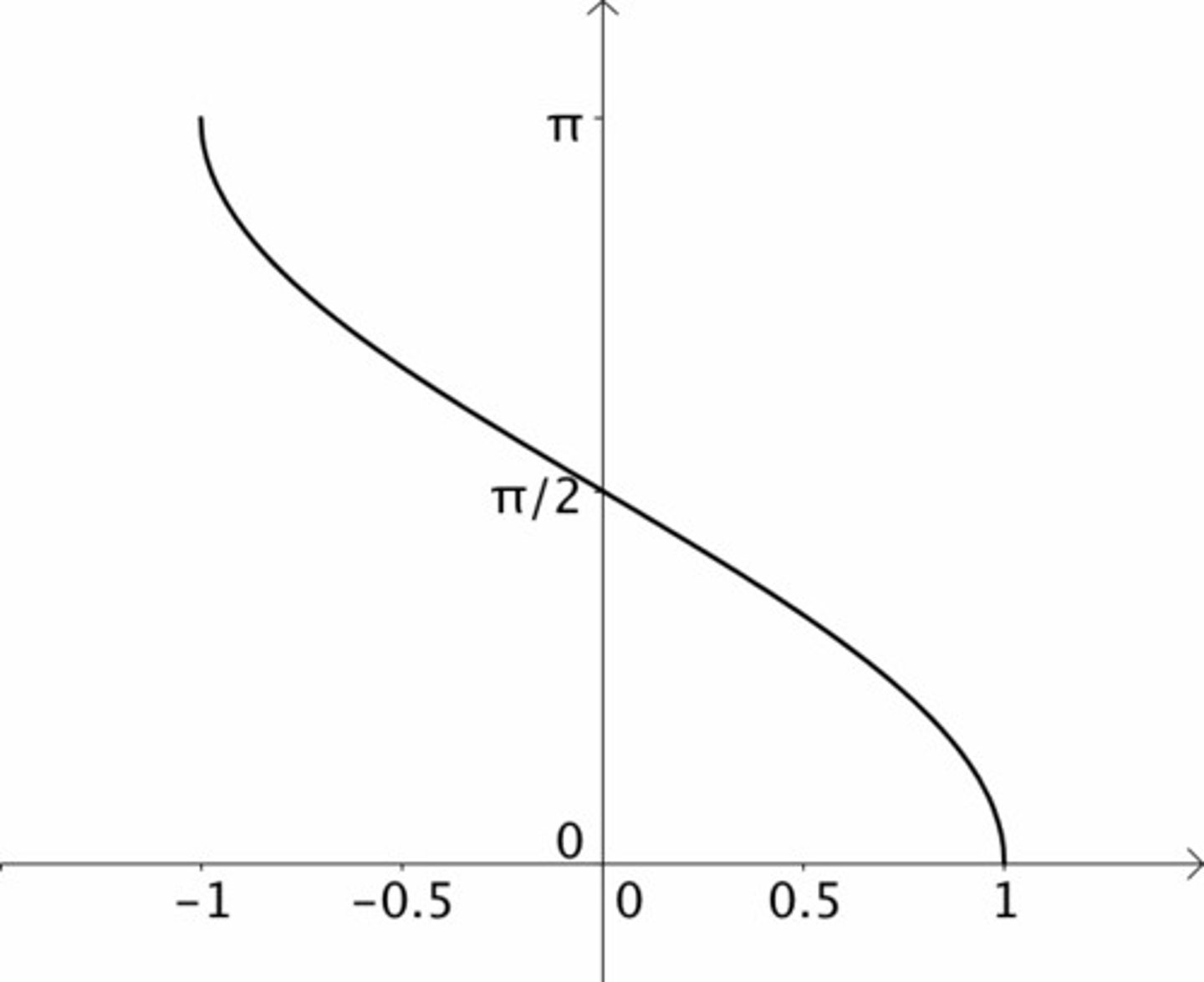
Arctan(x) Graph

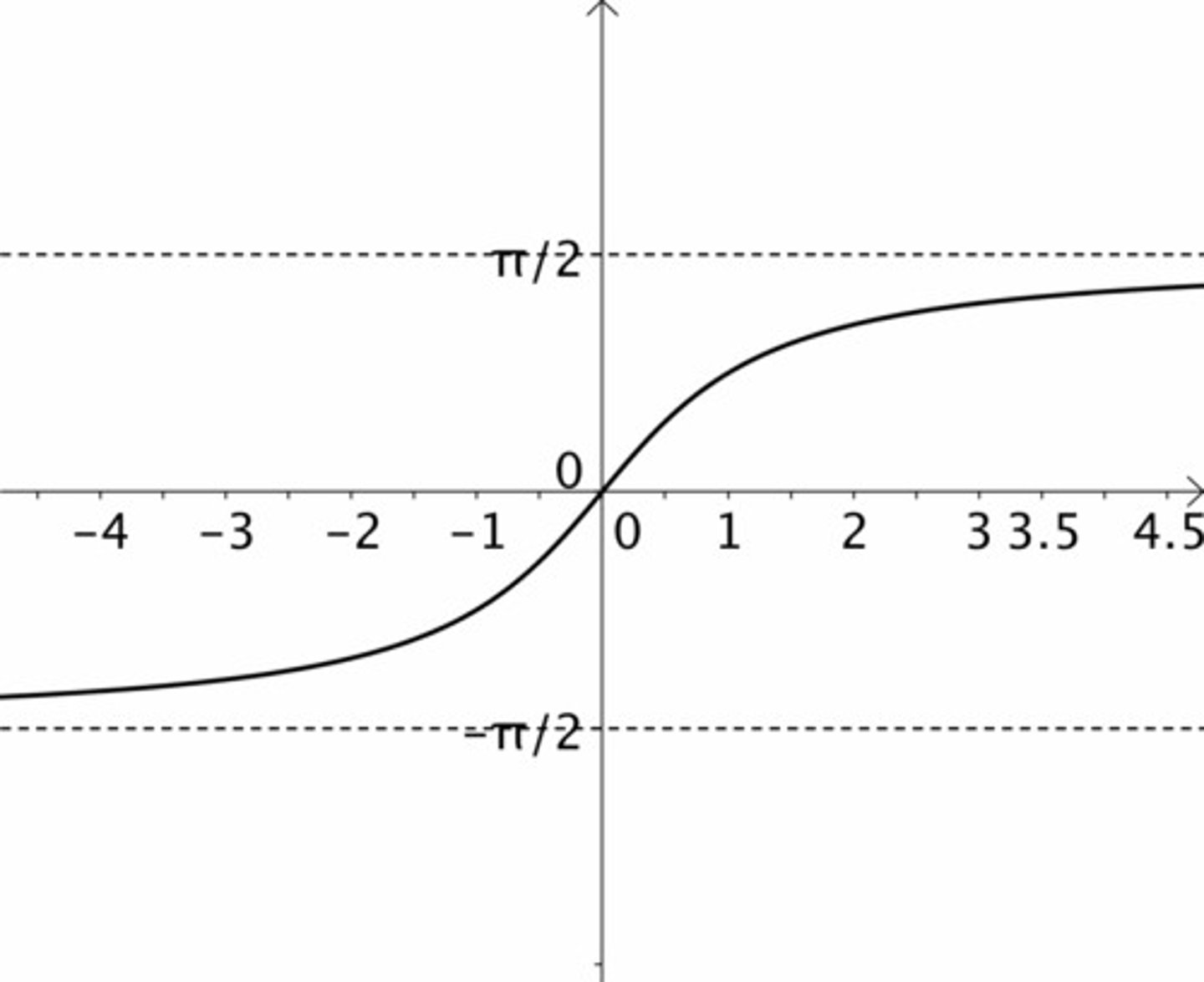
Differentiating y = eᵏˣ

dy/dx = keᵏˣ

Differentiating y = ln(x)

dy/dx = 1/x

Differentiating y = aᵏˣ

dy/dx = (aᵏˣ)kln(a)

The Chain Rule

dy/dx = dy/du x du/dx

The Product Rule

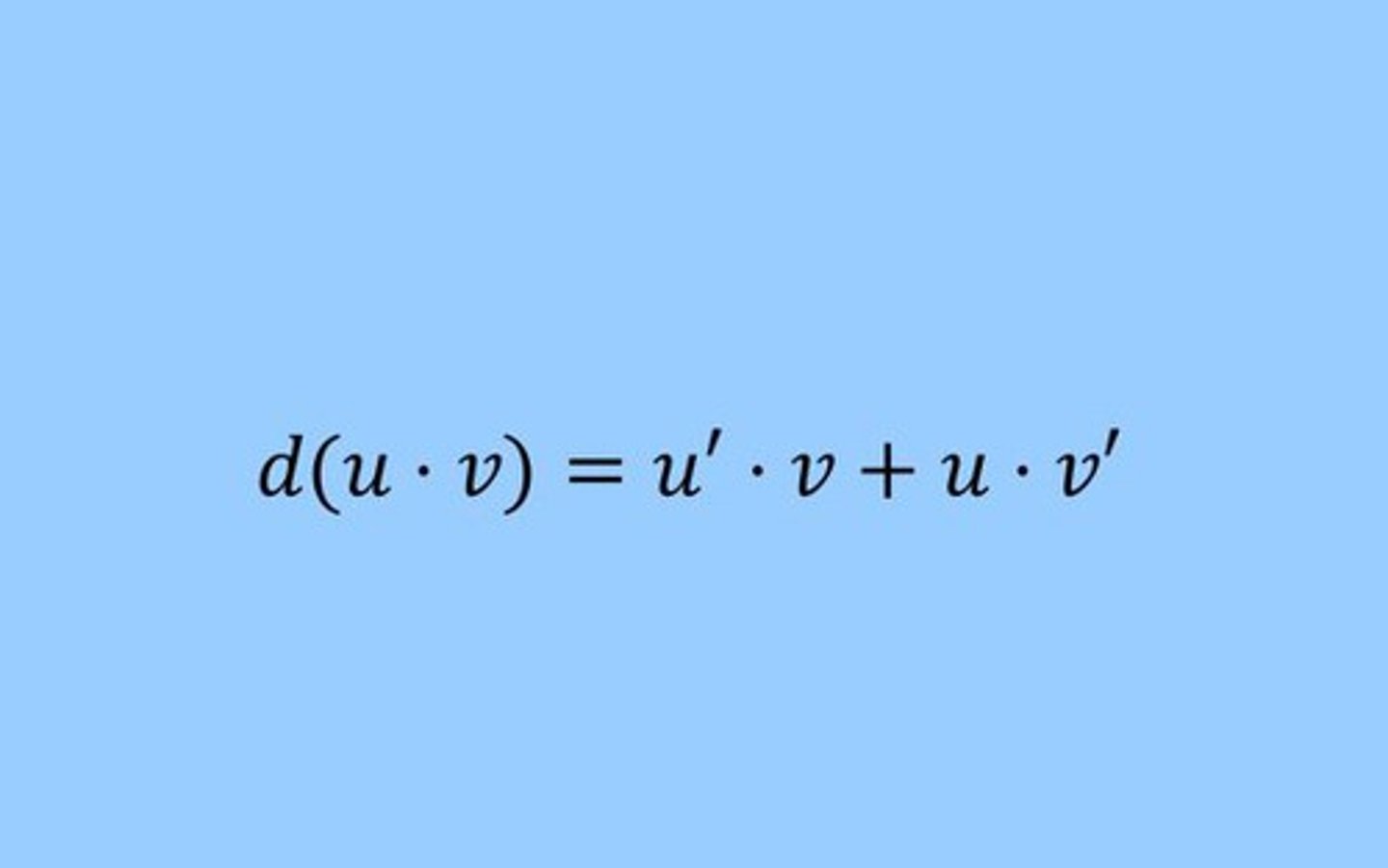
The Quotient Rule

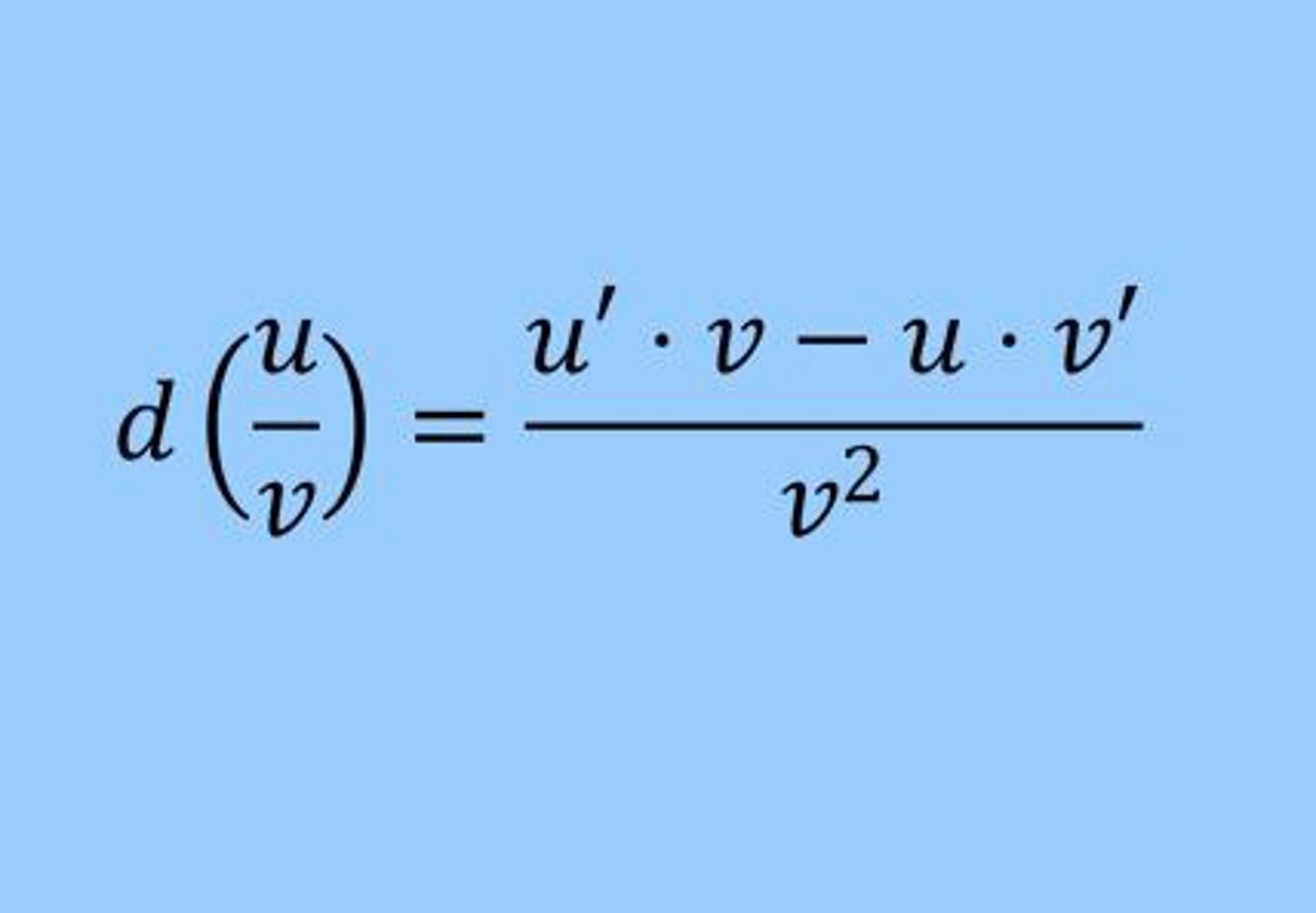
Differentiating parametric equations

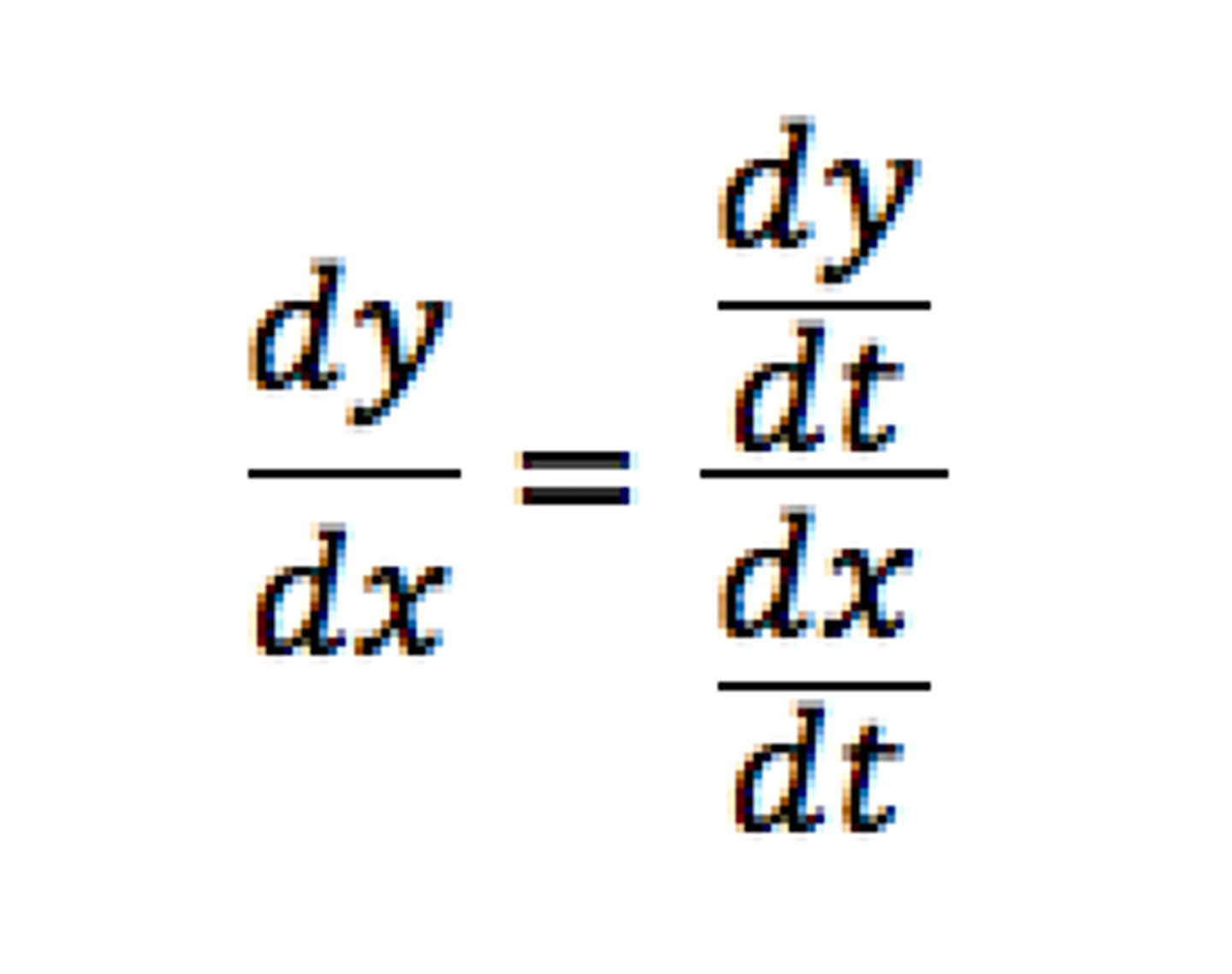
Implicit differentiation

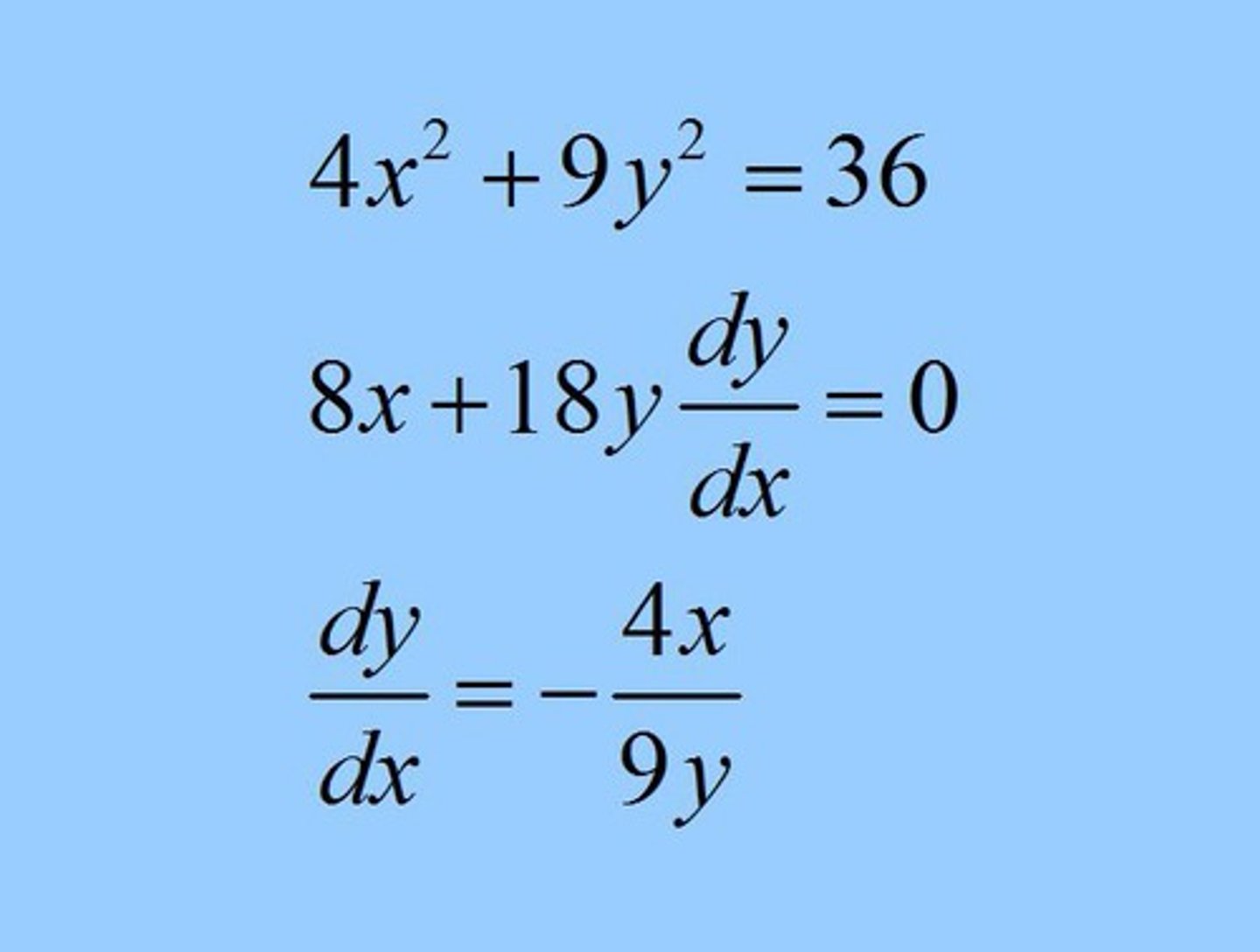
Concave function

f(x) concave if f''(x) ≤ 0 for all values of x in that interval

Convex function

f(x) concave if f''(x) ≥ 0 for all values of x in that interval

Point of inflection

Point at which f''(x) changes sign

∫ eˣ dx

eˣ + c

∫ 1/x dx

ln(x) + c

∫ sin(x) dx

-cos(x) + c

∫ cos(x) dx

sin(x) + c

Integration by parts

uv - ∫ v(du/dx) dx

1 + tan² θ

cot² θ + 1

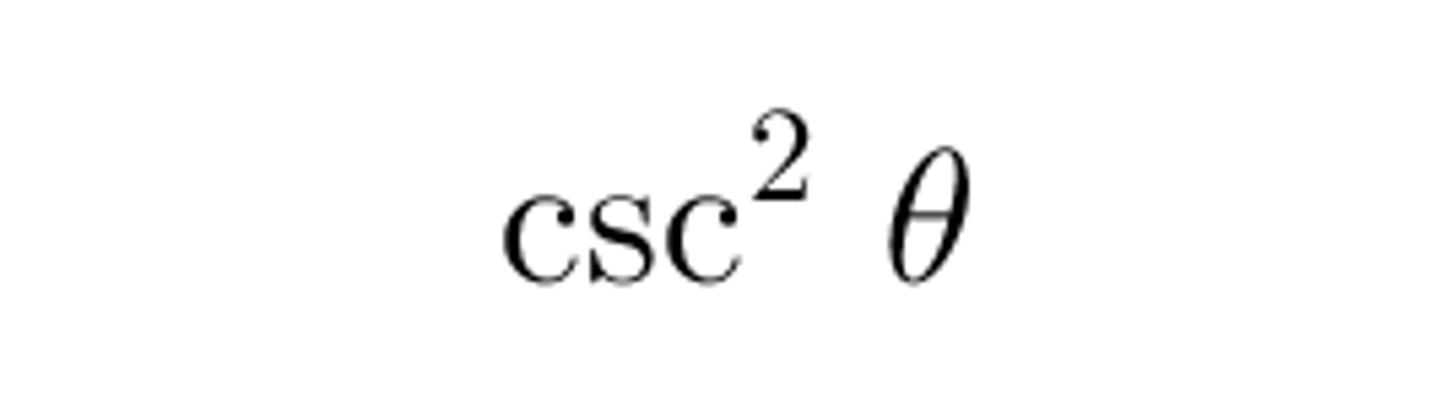
tan θ

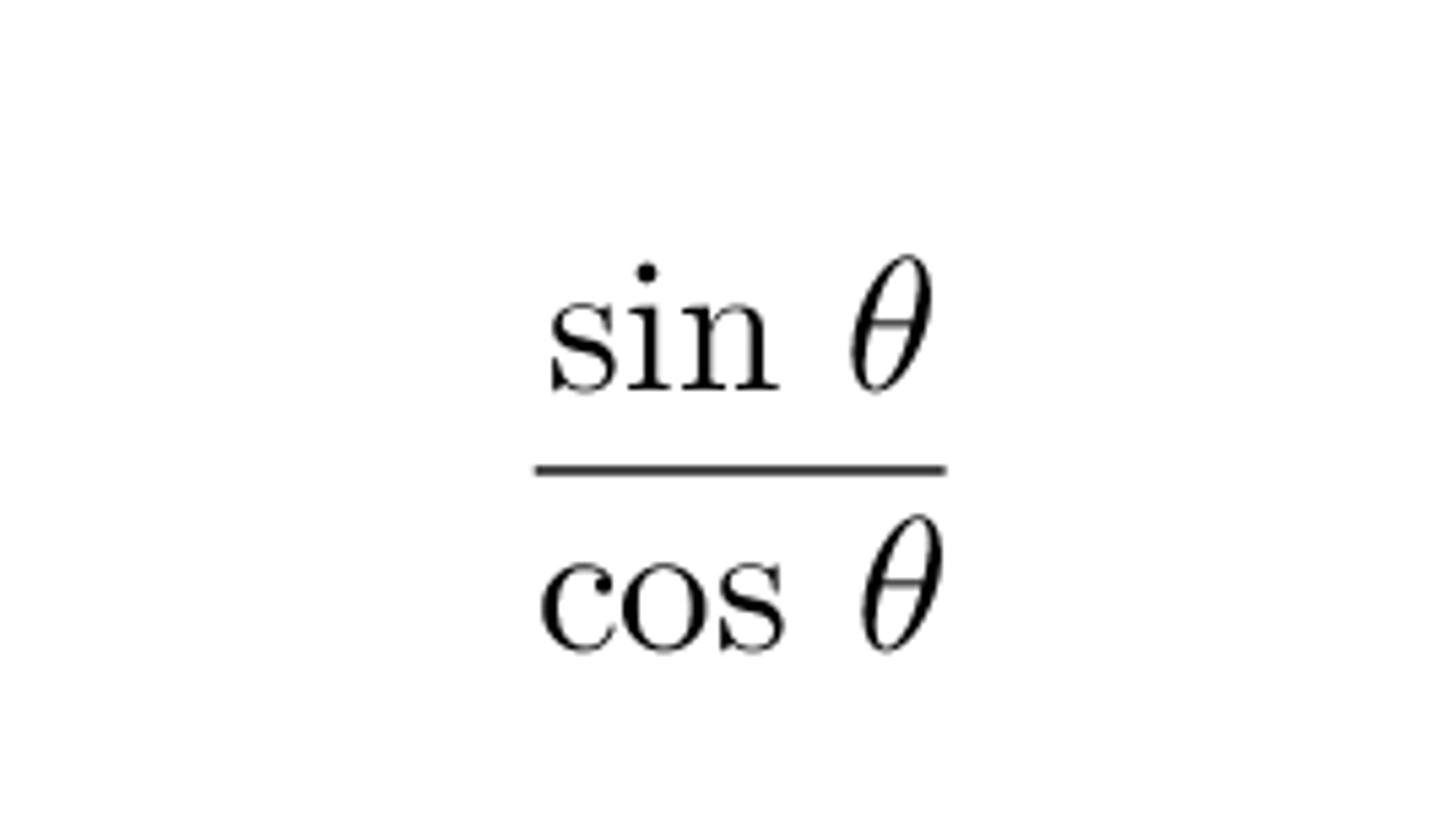
cot θ

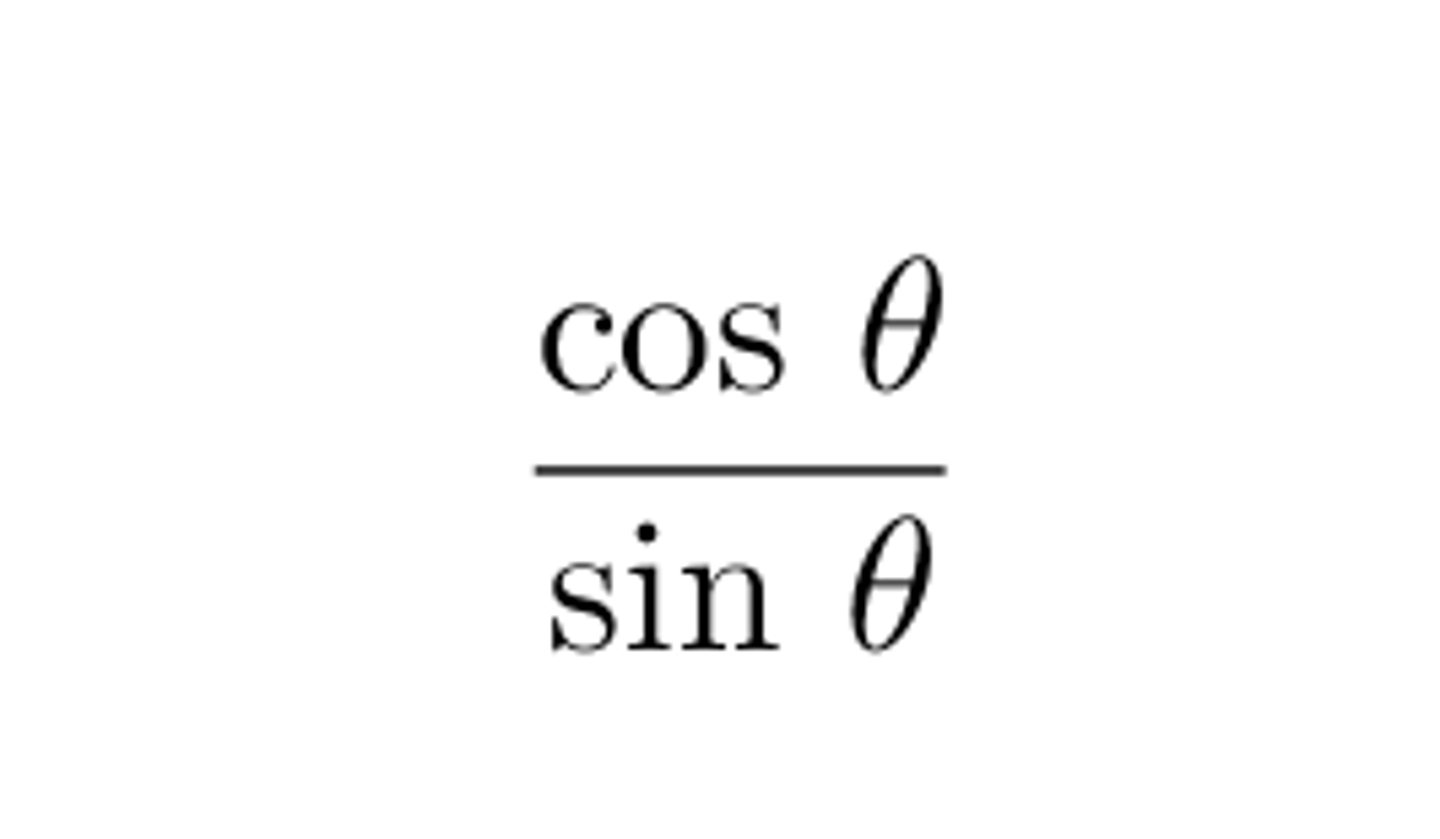
tan² θ

sec² θ - 1

1

sec² θ - tan² θ

cot² θ

csc² θ - 1

sin²θ+cos²θ=?

1

sec²x-1

tan²x

sec²x-tan²x

1

sin²x

1-cos²x

cos²x

1-sin²x

cot²x+1

csc²x

csc²x-cot²x

1

Pulley is smooth

- no friction
- therefore tension is uniform

String is inextensible

- acceleration is constant

string is light

- mass is negligable

linear regression

- do not extrapolate data
- should not use the linear regression line to find a value of x for a given y

experiment

- repeatable process
- rise to number of outcomes

event

A collection of one or more outcomes of an experiment

sample space

the set of all possible outcomes

Mutually exclusive events

P(A or B) = P(A) + P(B)
- cannot occur at same time , no overlap

independent events

P(A and B) = P(A) x P(B)

Probability mass function for B(n,p)

P(X = r) = (nCr)p^r(1-p)^n-r

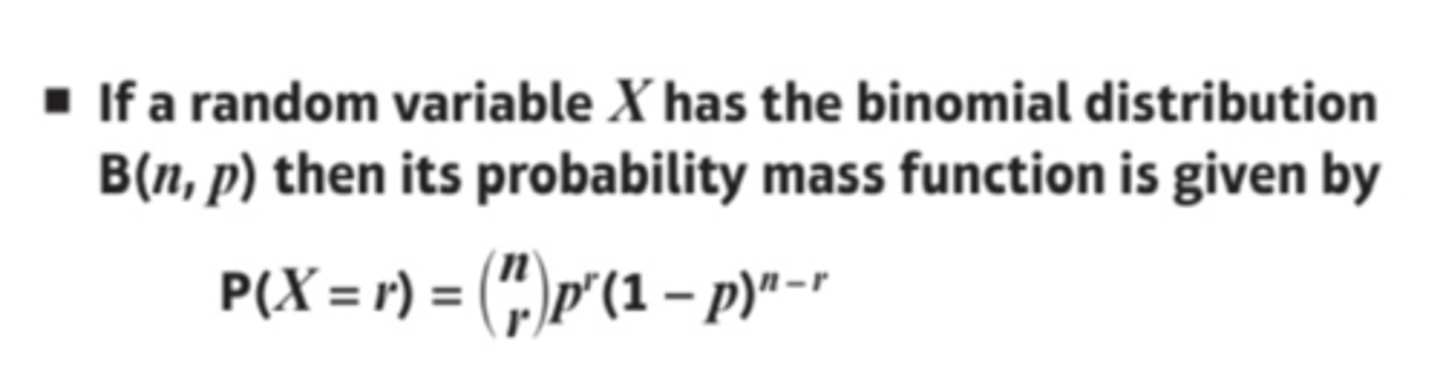
Model using binomial distribution when:

- fixed number of trials

- two possible outcomes

- fixed probability of success

- trials are independent of eachother

product moment correlation

Describes the linear correlation between two variables and takes a value between -1 - 1
-1 - strong negative correlation
0 no linear correlation
1 strong positive correlation

Explain why a linear model may be appropriate to describe the relationship between x and y.

As the points lie reasonably close to a straight line

Reliable estimate

when interpolation is used