lecture 8 hydrology

What does flood routing tell us?

a procedure to determine the outflow hydrograph at a downstream point of a river (or a reservoir) given the inflow hydrograph at an upstream point.

What does the shape of outflow hydrograph depend on ?

depends upon channel geometry, bed slope, length of channel reach, downstream control, initial channel flow, and upstream inflow hydrograph

When you have a wide rectangular channel with no lateral inflow, what does the continuity and moment equations look like (per unit width)

where H is the depth of flow, Q is the discharge = uH, u is the mean velocity of flow, So is the channel bed slope, Sf is the friction slope, g is the acceleration due to gravity, x is the space coordinate in the direction of flow, and t is time

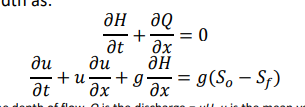
What are the forces acting upon the flood wave?

inertial, pressure, gravity, and friction

Forms of continuity equation

when using Hydraulic Routing, what assumptions are needed ?

uniform velocity distribution (depth averaged), hydrostatic pressure, small bottom slope

Mannings equation

An example of a hydrologic routing relation. Where n = roughness coefficient; A = cross sectional area of stream; Pwet = wetted perimeter (total length of stream bed from one bank to the opposite bank); R = hydraulic radius = A/Pwet; S = slope of river bed

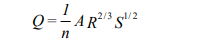
What is the Modified Puls Method used for?

Reservoir flood routing where outflow (Q) depends on water-surface elevation (H), and storage (S) is related to H.

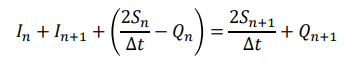
Muskingum Method

K = storage factor
X = weighting factor various between 0 and 0.5 (averages ~0.2)

Obtained by weighting the storage due to inflow (I) and outflow (Q) with X, assuming that discharge and storage are single-valued functions of depth, and that storage responds linearly to discharge

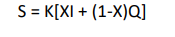
What do we get after substituting the storage equation into the continuity equation?

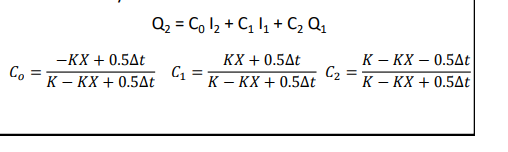
How do we estimate the value of K

The slop of this equation is K value

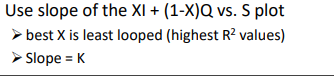
What are values of X for certain cases?

X = 0.0 when inflow I has no effect on storage
X = 0.2-0.3 are the most common for natural streams
X = 0.4-0.5 also for natural streams with little or no flood plains or storage effects
X = 0.5 represents equal weighting between inflow and outflow and would produce translation with little or no attenuation

Steps for modified Puls method

1. At the beginning of routing, inflow (I1 and I2 ), storage S1 , and outflow Q1 are known from initial reservoir conditions. Compute the left side of Eq.1, which equals (2S2 /Dt) + Q2 .

2. Determine Q2 or the graph (or table) of [2S/Δt + Q] vs. Q. This value of Q2 is instantaneous outflow at the end of ∆t.

3. Determine (2S2 /Dt) - Q2 by subtracting twice the value of Q2 of step 2. This gives the value of (2Sn /Dt) - Qn for the next time interval. Steps of Using Modified Puls Method

4. Add the two inflows I1 and I2 and the value in step 3. This gives (2Sn+1/Dt) + Qn+1 for the next time interval.

5. Determine Qn against (2Sn+1/Dt) + Qn+1 of step 4 using the graph of [2S/Δt + Q] vs. Q.

6. Determine (2Sn+1/Dt) – Qn+1 by subtracting twice the value of Qn of step 5. This gives the value of (2Sn /Dt) + Qn for the next time interval.

7. Go back to step 4 and repeat the procedure.