Standing Waves (Part-I)

Standing Wave

• A wave pattern formed by the superposition of two identical waves traveling in opposite directions

• Resulting in fixed nodes and antinodes with no net propagation of the wave pattern.

Resonance

A phenomenon in which a system oscillates with large amplitude when driven at a frequency equal to one of its natural frequencies.

Node

A fixed point in a standing wave where the displacement is always zero for all times.

Antinode

A point in a standing wave where the displacement oscillates with maximum amplitude.

Constructive Interference

Interference that occurs when waves are in phase, causing their amplitudes to add and produce a larger resultant amplitude.

Destructive Interference

Interference that occurs when waves are out of phase by π radians (180°), causing their amplitudes to cancel.

y(x, t) = 2Asin(kx)cos(ωt)

• Standing Wave Equation

• This equation describes a standing wave formed from two identical traveling waves moving in opposite directions.

In-Phase Condition (Standing Waves)

The condition when the two waves are in phase

t = n(T/2)

Value of the t, in the In-Phase Condition of the Standing Waves

Out-of-Phase Condition (Standing Waves)

The condition when the two waves are 180° out of phase

t = ((2n + 1)T)/4

Value of the t, in the Out-of-Phase Condition of the Standing Waves

Node Positions

Locations where

• sin(kx) = 0

• where x = n(λ/2)

• n = 1, 2, 3, ….

Antinode Positions

Locations where

• sin(kx) = ±1

• where x = n(λ/4)

• n = 1, 3, 5, ….

μ = dm/dx

Mathematical representation of Linear Mass Density

Linear Mass Density

Mass per unit length of a string

μ

Symbol that represents the Linear Mass Density

F_T

Symbol that Represents the Tension in the String

v = ((F_T)/μ)^1/2

Mathematical Representation of the Wave Speed on a String

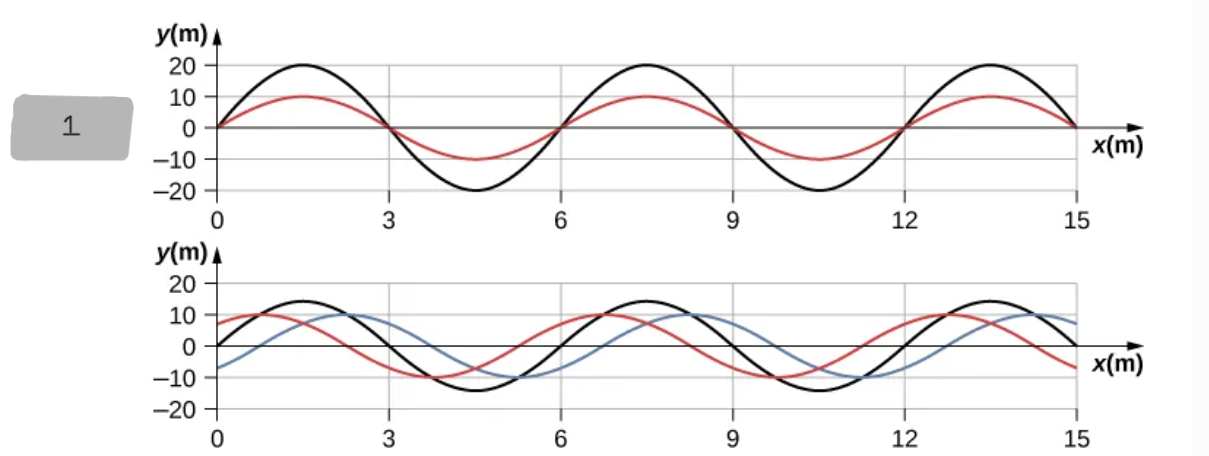
t = 0T

(1)

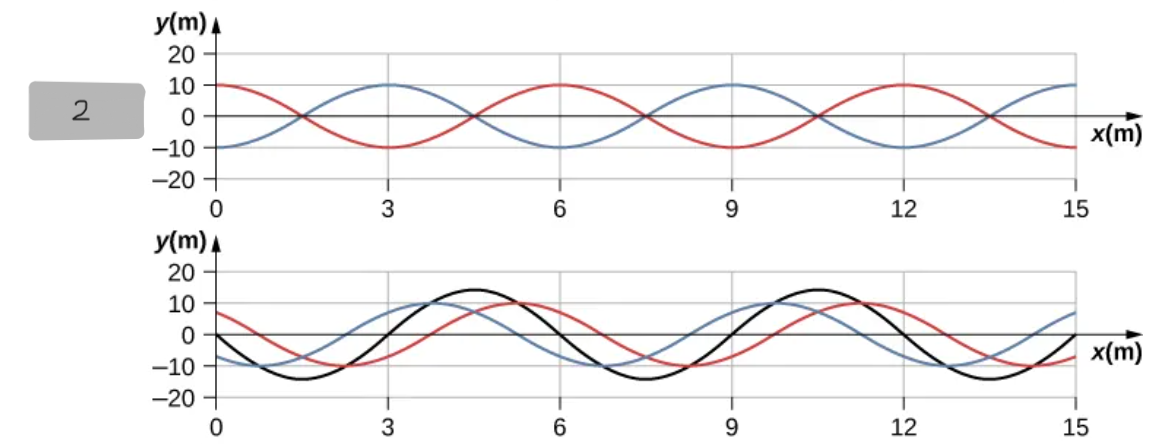
t = (1/4)T

(2)

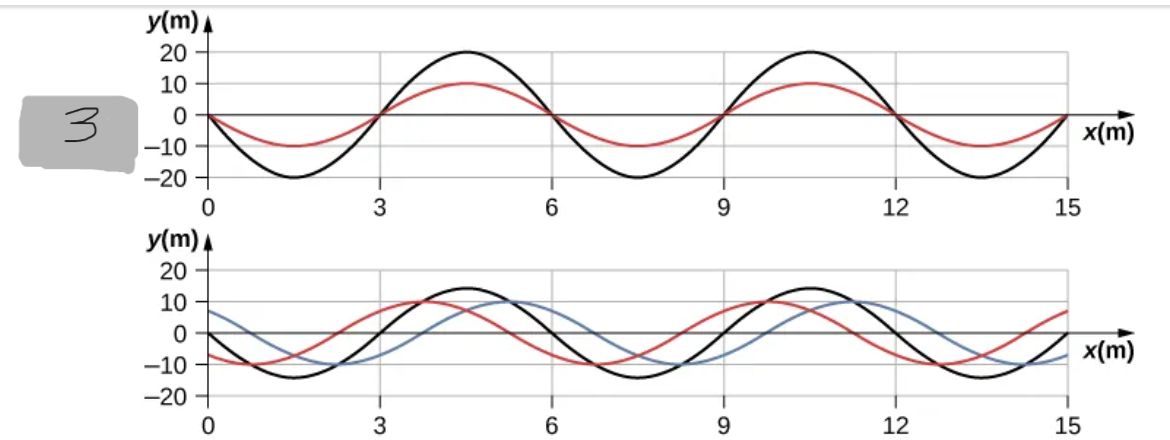
t = (1/2)T

(3)

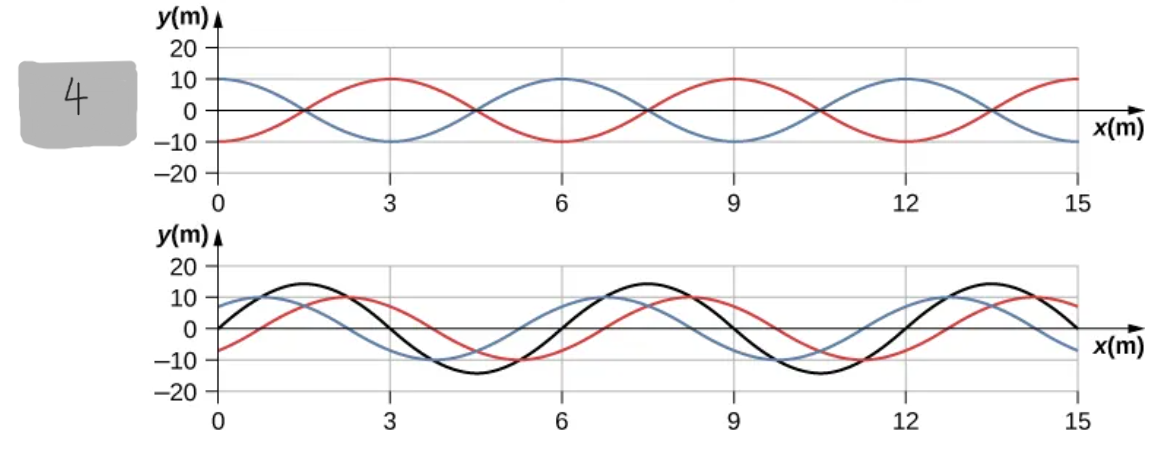
t = (3/4)T

(4)

String Vibrator

(i)

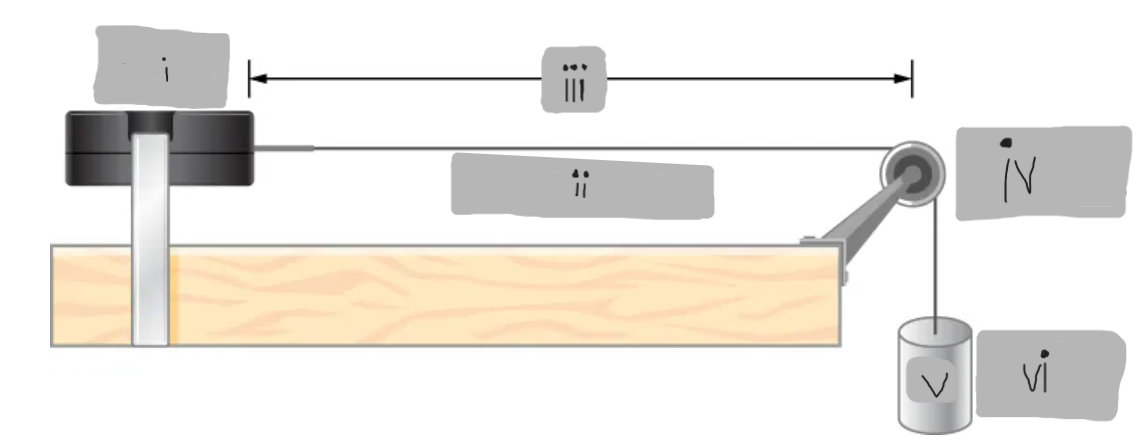
μ = dm/dx = constant

(ii)

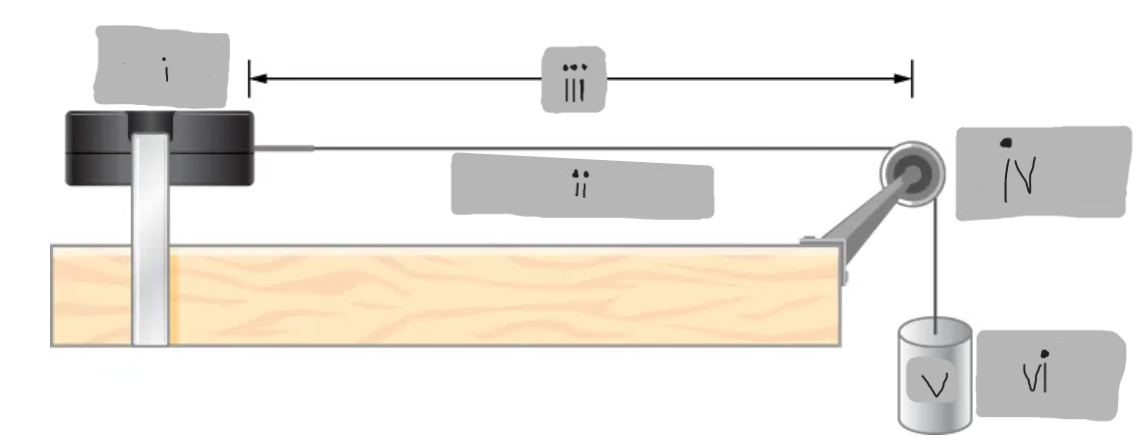
L

(iii)

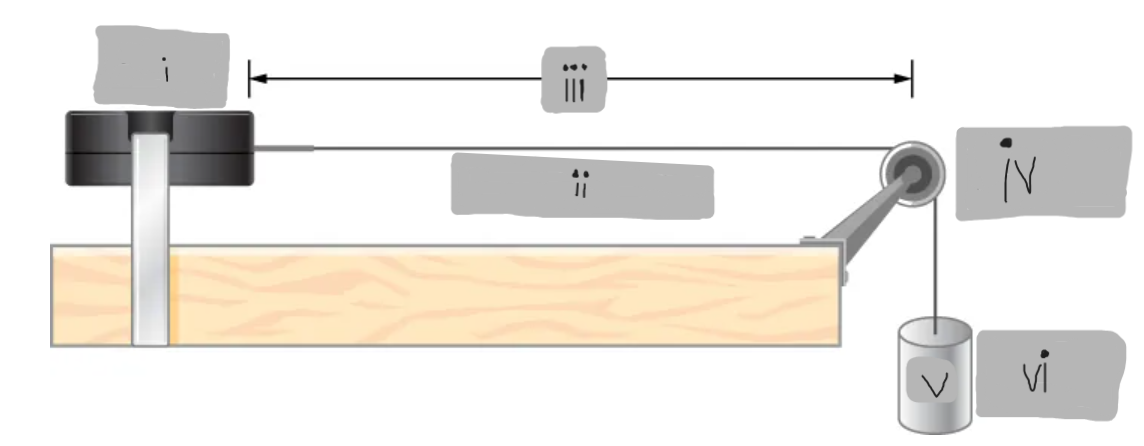
Frictionless Pulley

(iv)

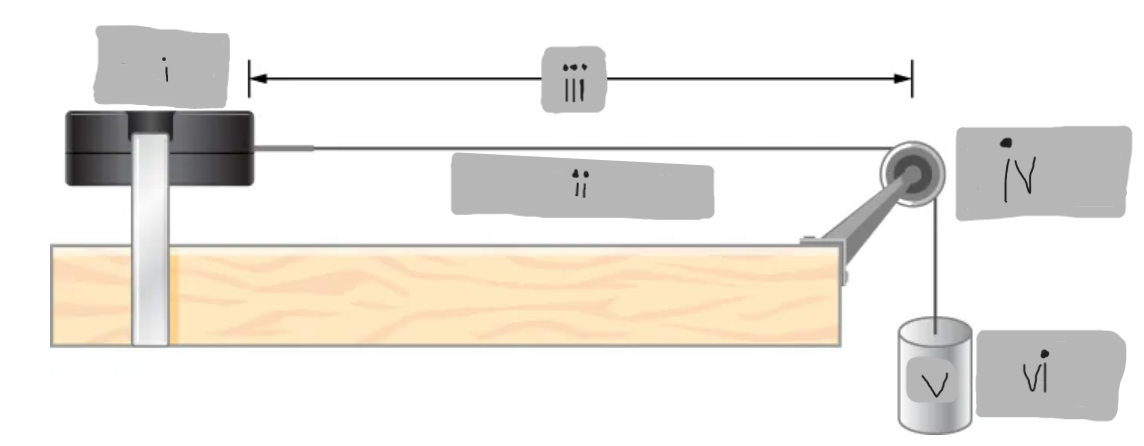
m

(v)

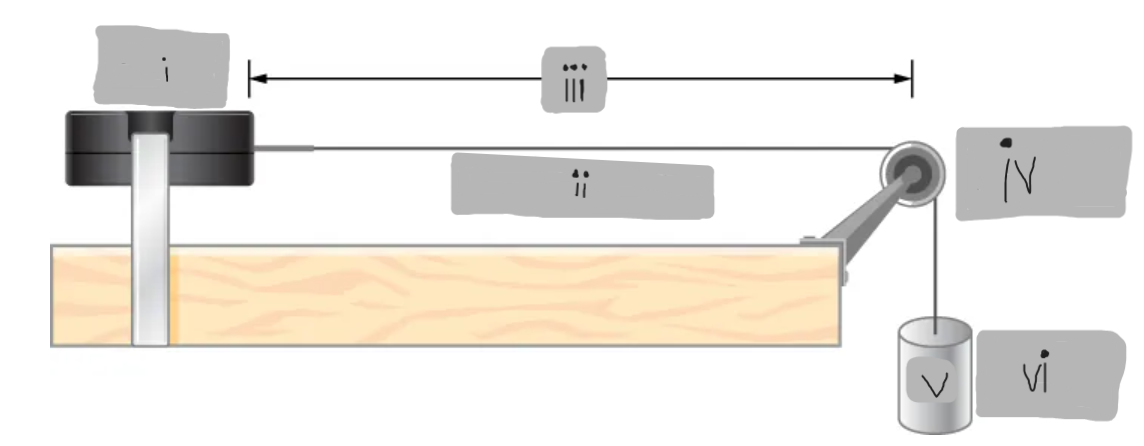
Hanging Mass

(vi)

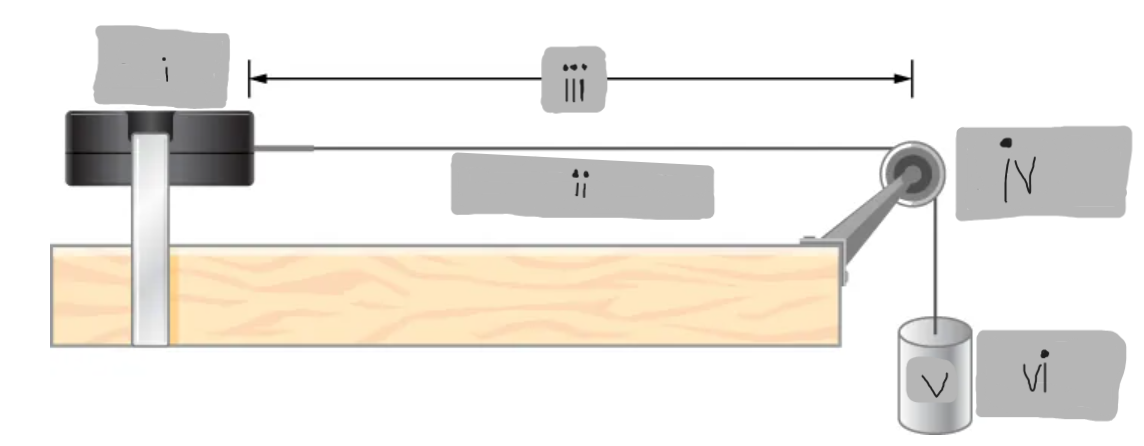
Boundary Conditions (Fixed Ends)

Conditions where both ends of a string are fixed, forcing nodes to exist at both ends.

Fundamental Mode (First Harmonic)

The lowest-frequency standing wave mode, where half a wavelength fits in the string length

λ1 = 2L

Mathematical Representation of the Fundamental Mode

f1 = v/(2L)

Fundamental Frequency: The frequency corresponding to the first harmonic.

Harmonic Number (Mode Number)

An integer n that labels standing wave patterns, with higher values corresponding to higher frequencies and more nodes.

f_n = (nv)/(2L)

Mathematical Representation of the nth Harmonic Frequency (String)

λ_n = (2L)/n

Mathematical Representation of nth Harmonic Wavelength (String)