Ch 7 linear regression

what is regression analysis?

what is regression analysis?

if data is obtained, a statistical procedure called regression analysis can be used to develop an equation showing how the variables are related.

what is a dependent variable?

the variable being predicted, in statistical notation: y = dependent variable

what is an independent variable or predictor variable?

variables being used to predict the value of the dependent variable. in statistical notation: x = independent variable

what is linear regression?

a regression analysis involving one independent variable and one dependent variable.

what is simple linear regression?

a regression analysis for which any one unit change in the independent variable, x, is assumed to result in the same change in the dependent variable, y.

what is the multiple linear regression?

regression analysis involving two or more independent variables.

what is the simple linear regression model?

• the equation that describes how y is related to x and an error term

• simple linear regression model: y = B₀+B₁+E

• parameters: the characteristics of the population, B₀ and B₁

• random variable: error term, E

• the error term accounts for the variability in y that cannot be explained by the linear relationship between x and y

what is estimated regression:

• the parameter values are usually not known and must be estomated using sample data

• sample statistics (denoted b₀ and b₁) are computed as estimates of the population B₀ and B₁

• the equation obtained by substituting the values of the sample statistics b_o and b₁ for B_o and B₁ in the regression equation.

what is the estimated simple linear regression equation:

• y^ = b_o + b₁x

• y^ = point estimator of E(y|x)

• b_o = estimated y-intercept

• b₁ = estimated slope

• the graph of the estimated simple linear regression equation is calles the estimated regression line

what is the estimated regression line?

the graph of the estimated simple linear regression equation

possible lines in simple linear regression:

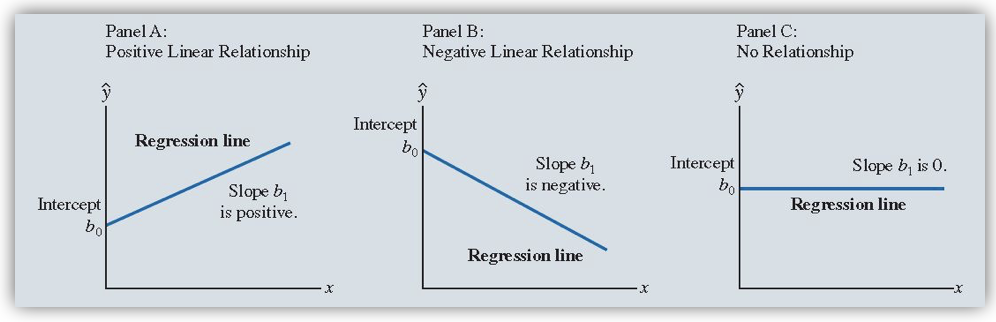
what is the least squares method?

• a procedure for using sample data to find the estimated regression equation

• determine the values of b_o and b₁

what is the inteprestation on b_o and b₁ in the least squares method?

• the slope b₁ is the estimated change in the mean of the dependent variable y that is associated with a one unit increase in the independent variable x

• the y-intercept b_o is the estimated value of the dependent variable y when the independent variable x is equal to zero.

what is the ith residual?

• the error made using the regression model to estimate the mean value of the deoendent variable for the ith observation

  • denoted as e_i = y_i - y^

  • we are finsing the regression that minimizes the sum of squared errors

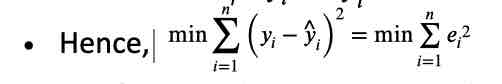
what is an experimental region?

the range of values of the independent variables in the data used to estimate the model

• the regression model is valid only over this region

what is the sum of squares due to error (SSE)?

the value of SSE is a measure of the error in using the estimated regression equation to predict the values if the dependent variable in the sample.

SSE = e_i²

what is the total sum of squares (SST)?

the difference y_i - y- provides a measure of the error involved in using y^- to predict travel time for the ith term. SST = (y_i - y^-)²

what is sum of squares due to regression (SSR)?

measures how much the y^ values on the estimated regression line deviate from y^- . relation between SST, SSR, and SSE: SST = SSR + SSE

what is the coefficient of determination?

• the ratio SSR/SST used to evalute the goodness of fit for the estimated regression equation.

• r² = SSR/SST

• take values between zero and one

• interpreted as the percentage of the total sum of squares that can be explained by using the estimated regression equation

• square of the correlation between y_i and y^_i

• referred to as the simple coefficient of determination in simple regression

what is slope coefficient B_j?

represents the change in the mean value of the dependent variable y that corresponds to a one unit increase in the independent variable x_j, holding the values of all other indpendent variables in the model constant.

what is the multiple regression equation that describes how the mean value of y is related to x_1, x₂, … , x_q?

E( y | x₁, x₂, … , x_q = B₀ + B₁x₁ + B₂x₂ + … + B_qx_q

what is statistical inference?

process of making estimates and drawing conclusions about one or more characteristics of a population (the value of one or more parameters) through the analysis of sample data drawn from the population

in regression, inference is commonly used to estimate and draw conclusions about:

• the regression parameters B₀, B₁, B₂, … , B_q

• the mean value and/or the predicted value of the dependent variable y for specific values of the independent variables x₁*, x₂* , …, x_q*

• consider both hypothesis testing and interval estimation

conditions necessary for valid inference in the least squares regreesion model:

1. for any combination of values of the independent variables x₁, x₂, …, x_q

2. the values of e are statistically independent

testing individual regression parameters:

• to determine whther statistically significant relationships exist between the dependent variable y and each of the indpendent variables x₁, x₂, … , x_q individually

  • if B_j = 0, there is no linear relationship between the independent variable y and the independent variable x_j

  • if B_j ≠ 0, there is a linear relationship between y and x_j

what is a confidence interval?

an estimate of a population parameter that provides an interval believed to contain tha value of the parameter at some level of confidence

what is a confidence level?

indicates how frequently interval estimates based on samples of the same size taken from the same population using identical sampling techniques will contain the treu value of the parameter we are estimating

addressing nonsignificant independent variables:

• if practical experiences dictates that the nonsignificant indpendent variable has a relationship with the dependent variable, the independent variable should be left in the model

• if the model sufficiently explains the dependent variable without the nonsignificant independent variable, then consider rerunning the regression without the nonsignificant independent variable

• the appropriate treatment of the inclusion of exculsion of the y-intercept when b₀ is not statistically significant may require special consideration

testing for an overall regression relationship:

• us an F-test based on the F probability distribution

• if the F-test leads us to reject the hypothesis that the values of B₁, B₂, …, B_q are all zero:

  • conclude that there is an overall regression relationship

  • otherwise, conclude that there is no overall regression relationship