223 definitions

the pivot of a row matrix is

the left most non zero entry in that row

a matrix is in row echelon form if

1. all rows consisting only of 0’s are at bottom

2. pivot if each non zero is in a column to the right of the pivot in the row above it

a matrix is in reduce row echelon form if

1. the matrix is in row echolon form 

2. the pivot in each row is equal to 1

3. each pivot is the only non zero entry on its column

we say x_i is a basic variable for the system if

the ith column of rref(c) has a pivot 

we say the x_i is a free variable for the system if

the ith column of the rref(c) does not have a pivot

the system if inconsistent if and only if

the last column of rref(A) has a pivot

The system has exactly one solution if and only if 

the last column does not have a pivot and every other column of rref(c) has a pivot 

the system has infinitely many solutions if and only if 

the last column of the rref(c) does not have a pivot and rref(A) has a column without a pivot 

a linear combination of vectors v₁, v₂,…,v_n in Rⁿ is a vector of the form 

c₁v₁, c₂v₂,…,c_nv_n

the span of vectors of v₁, v₂,…,v_n in R^m is the set 

span (v₁, v₂,…,v_n) = {c₁v₁₊…+c_nv_n| c₁, c₂…,c_n ∈ R}

a set of vectors {v₁, v₂,…,v_n} in R^m

At least one of the vectors is a linear combination of others: that is v_i ∈ span(v₁, v₂,…,v_i-1, v_i+1,...v_n)

a vector space (over the real numbers) is any set of vectors V in Rⁿ that satisfies all of the following properties:

1. V is non empty

2. V is closed under scalar multiplication

3. V is closed under vector addition

let V be a vector subspace of Rⁿ. A spanning set (also known as a Generating Set) for V is

any subset B of V so that V = span(B)

a subset B of a vector space V is called a Basis if

1. B is a spanning set and 

2. B is linearly independent 

Let V be a nonzero vector subspace of Rⁿ. Then the dimension of V, denoted dimV, is 

the size of any basis for V 

the standard basis for R is the set E :={e₁, e₂ , . . .,e_n } where e_i is

the vector in n dimensional space where 1 in the ith coordinate and 0 in all other coordinate 

Let A be an mxn matrix with column vectors A = (v₁ v₂ · · · v_n). Then, for a vector x in Rⁿ the matrix-vector product of A and x is the vector in R^m defined by

Ax = x₁v₁ + x₂v₂+ … + x_nv_n

Let A be an mxn matrix. Then, the matrix transformation associated to A is the function

T_A : Rⁿ → R^m defined by T_A(x) = Ax

A function F: Rⁿ → R^m is called linear if it satisfies the following two properties for all vectors v,w ∈ Rⁿ and scalars c ∈ R

1. F(v + w) = F(v) + F(w)

2. F(cw) = cF(w)

Let F: Rⁿ → R^m be a linear transformation. Then, the defining matrix of F is the mxn matrix M satisfying

F(x) = Mx

A function f: X →Y is called one-to-one (or injective) if the following property holds

for all y ∈ Y there is at most one input x ∈ X so that f(x) = y

A function f: X →Y is called onto (or surjective) if the following property holds

for all y ∈ Y there is at least one input x ∈ X so that f(x) = y

A function f : X → Y is called bijective if

f is both injective and surjective

Let V be a subspace of Rⁿ and W a subspace of R^m. An isomorphism between V and W is

any linear bijective function F: V → W

The kernel of F is the subset ker(F) ⊆ Rⁿ defined by

ker(F) := {x ∈ Rⁿ: F(x) = 0} ⊆ Rⁿ

The image of F is the subset im(F) ⊆ R^m defined by

im(F) := {F(x): x ∈ Rⁿ} ⊆ R^m

The Rank of F is

the dim of im(F)

The Nullity of F is

the dim of ker(F)

The column space of A is the subspace of R^m given by

Col(A) := Span(v₁, v₂,…,v_n)

The Null space of A is the subspace of Rⁿ given by

Nul(A) := {x∈ Rⁿ : Ax = 0}

The nullity of A is

the dimension of Nul(A)

The Rank of A is

the dimension of Col(A)

A system of linear equations is called homogeneous if

the constatnt coeff in every equation is 0

The sum of A and B is the mxn matrix given by

A + B:= (v¹+w¹ v²+w² … vⁿ+wⁿ)

The scalar product of A with C is the mxn matrix given by

cA: = (cv₁ cv₂ … cv_n)

Let A be an mxk matrix and B = (b₁ · · · b_n)
be a kxn matrix. Then, the matrix product of A and B is the mxn matrix

AB:= (Ab₁ Ab₂ … Ab_n)

the identity matrix I_n is

nxm I_n = (x₁ x₂ …x_n)

that is I_n = [(1 0 … 0), (0 1 … 0), (0 0 …1)]

Let A be an nxn matrix. The inverse of A, if it exists, is

the matrix B such that AB = I_n and BA = I_n (not always the same though)

An n x n matrix is called elementary if

it can be obtained by performing exactly one row operation to the identity matrix 

The unit square is the subset of R² given by

S := {α1e1 + α2e2 : 0 ≤ α1, α2 ≤ 1}.

An ordered basis {b1,b2} for R² is called positively oriented if

we can rotate b1 counterclockwise to reach b2 without crossing the line spanned by b2. Otherwise, the basis is called negatively oriented.

Let F: R² → R² be a linear transformation. Then, the determinant of F, denoted by det(F), is the oriented area of F(S). That is,

det(F) :=

area(F(S)) if {F(e1), F(e2)} is positively oriented

−area(F(S)) if {F(e1), F(e2)} is negatively oriented

0 if area(F(S)) = 0.

If A is a 2 × 2 matrix, the determinant of A, denoted by det(A),

det(A) := det(TA)

The unit cube is the subset of R³ given by

C := {α1e1 + α2e2 + α3e3 : 0 ≤ α1, α2, α3 ≤ 1}.

For an n × n matrix A =(aij)

the ij-minor of A is defined to be the (n − 1) × (n − 1) matrix A(ij) with the ith row and jth column deleted.

Let A be the n × n matrix with ij-entry equal to aij . Then we define the determinant of A by the following cofactor expansion formula:

det(A) := a11 det(A11) − a12 det(A12) + · · · + (−1)n+1a1n det(A1n)

Let A be an n×n matrix. A non-zero vector v is an eigenvector

of A if

Av = λv where 

Let A be an n × n matrix with eigenvalue λ.

(1) The λ-Eigenspace of A is the vector subspace of R

n defined by

Eλ := Nul(A − λIn).

The geometric multiplicity of λ

the dimension of the λ-eigenspace Eλ.

For an n × n matrix A, the characteristic polynomial of A is called

χA(x) = det(A − xIn).

Let B = {v1, v2,…, vn} be an ordered basis for a vector space V.

Recall that every vector x in V can be written in the form

x = x1v1 + · · · + x_nv_n

The B-coordinates of x is the vector in Rⁿ given by

[x]_B :=

(x1

.

.

.

xn)

Let C and B be bases for a vector space V . Then, the change

of basis matrix MC←B is the matrix satisfying

M_C←B[x]_B = [x]_C

Let C be a basis for a vector space V . Then, for any x, y ∈ V and scalar k ∈ R we have

[x + y]_C = [x]_C + [y]_C and [kx]_C = k[x]_C.

Let {b1, . . . ,bn} be a linearly independent subset of a vector space V .

Then, for any basis C of V , the set {[b1]C, . . . , [bn]C}

is linearly independent 

Let F: Rⁿ→Rⁿ be a linear transformation, and B be any basis for R^n. Then, the defining matrix of F with respect to the basis B is the matrix M so that…

[F(x)]_B = M[x]_B
we use the notation M = M_F,B

Twon×nmatrices B and C are called similar if they represent the same function, but in possibly different bases.That is

there is a single linear transformation F:Rⁿ→Rⁿ so that M_F,B = B and M_F,C =C where B and C are bases for Rⁿ

An n×n matrix D is called diagonal if

the only non zero entries in the matrix appear on the diagonal. That is

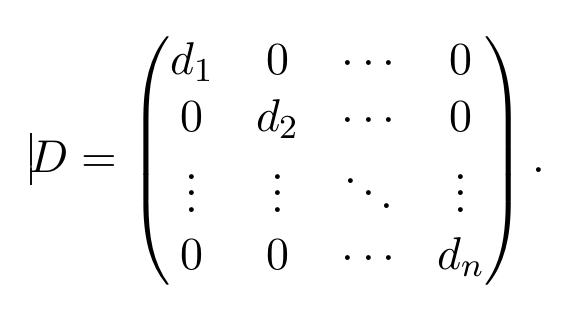
In this case we write D = diag(d1, d2,…dn)

An n×n matrix is called diagonalizable if

it is similar to a diagonal matrix

Suppose that A is an n×n diagonalizable matrix with eigenvalues λ1,...,λn and corresponding linearly independent eigenvectors v1,...,vn. We call the equality

A = CDC^-1

the EIGENDECOMPOSITION of the matrixA. By the Diagonalization Theorem, we know that

D=diag(λ1,...,λn) and C= (vector)v1 ··· (vector)vn

The dot product of vector u and v is the scalar

u (dot) v = u1v1 + u2v2 + …+ unvn

Let vector uand v be vectors in Rⁿ

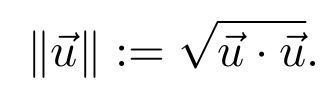
The distance between vectors u and v is

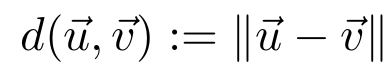
We say that u and v are orthogonal if

u (dot) v = 0

A basis B={v1,v2,...,vn} is orthogonal if

vector u_i (dot) v_j for every i ≠ j

An basis B is called orthonormal if it’s orthogonal and

||v_i|| = 1 for every v_i in B

We call an n×n matrix Q orthogonal if

its column vectors form an orthonormal basis for Rⁿ

Equivalently, Q is called orthogonal if Q^T = Q^-1

For vectors x, y in Rⁿ, the orthogonal projection of x onto y is

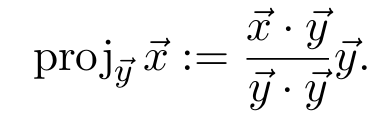
An n×n matrix A is called orthogonally diagonalizable if

there exists an orthogonal matrix Q and a diagonal matrix D so that Q^⊤AQ = D

Suppose that A is an n×n symmetric matrix with eigenvalues λ1,...,λn and orthonormal basis of eigenvectors{v1,...,vn}. We call the equality

A = QDQ^T

a SPECIAL DECOMPOSITION of A, where

D = diag{λ₁,...,λ_n} and Q = (v₁ … v_n)

Let A be an m×n matrix and {v1,...,vn} be an orthonormal basis for Rⁿ of eigenvectors for A^⊤A, as above. The singular values of A are

the scalars σ_i = ||Av_i|| for i = 1,…,n