Chapter 11 Exercises: Conditional Proofs (Symbolic Logic)

conditional proof

a method of proof that involves making an assumption

• used to prove ANY conditional statement

• could be the conclusion of the argument or an intermediate step

1. Indent and make an assumption.

   1. Justification is ACP: assumption for conditional proof.

2. Derive the consequent of the conditional using the rules we’ve already introduced.

3. After you reach the consequent, return to the left margin and write the conditional, using the indented lines and CP for the justification.

How is a conditional proof constructed?

True

True or False: No valid proof may end on an indented line.

True

True or False: Once an assumption has been discharged, no indented line within the conditional proof may be used to justify any later step in the proof.

True

True or False: Any earlier line on the left margin of your proof (or above the current line within the same conditional proof) may be used to help justify the next line of your conditional proof.

False

True or False: Conditional proof may only be used when the (overall) conclusion of thea rgument you’re trying to prove is a conditional.

True

True or False: A single proof can contain multiple conditional proofs.

False

True or False: When you derive a line such as R within a conditional proof, what you’ve shown is that R is validly entailed by the premises of the argument. 

True

True or False: When you derive a line such as R within a conditional proof, what you’ve shown is that if the premises and your assumption were all true, then R would have to be true also.

1. (G ∨ T) ⊃ O           /G ⊃ O

      2. G                       [ACP]

      3. G ∨ T                [2, Add]

      4. O                       [1, 3 MP]

5.  G ⊃ O                  [2-4 CP]

What justifications should appear in the blanks in the proof below?

1. (G ∨ T) ⊃ O           /G ⊃ O

      2. G                       (?)

      3. G ∨ T                (?)

      4. O                       (?)

5.  G ⊃ O                     (?)

True

True or False: The proof below is correct.

1. A                         /B ⊃ A

Indent/ 2. B                 ACP

Indent/ 3. A ∨ A           1, Add

Indent/ 4. A                   3, Taut

5. B ⊃ A                        2-4, CP

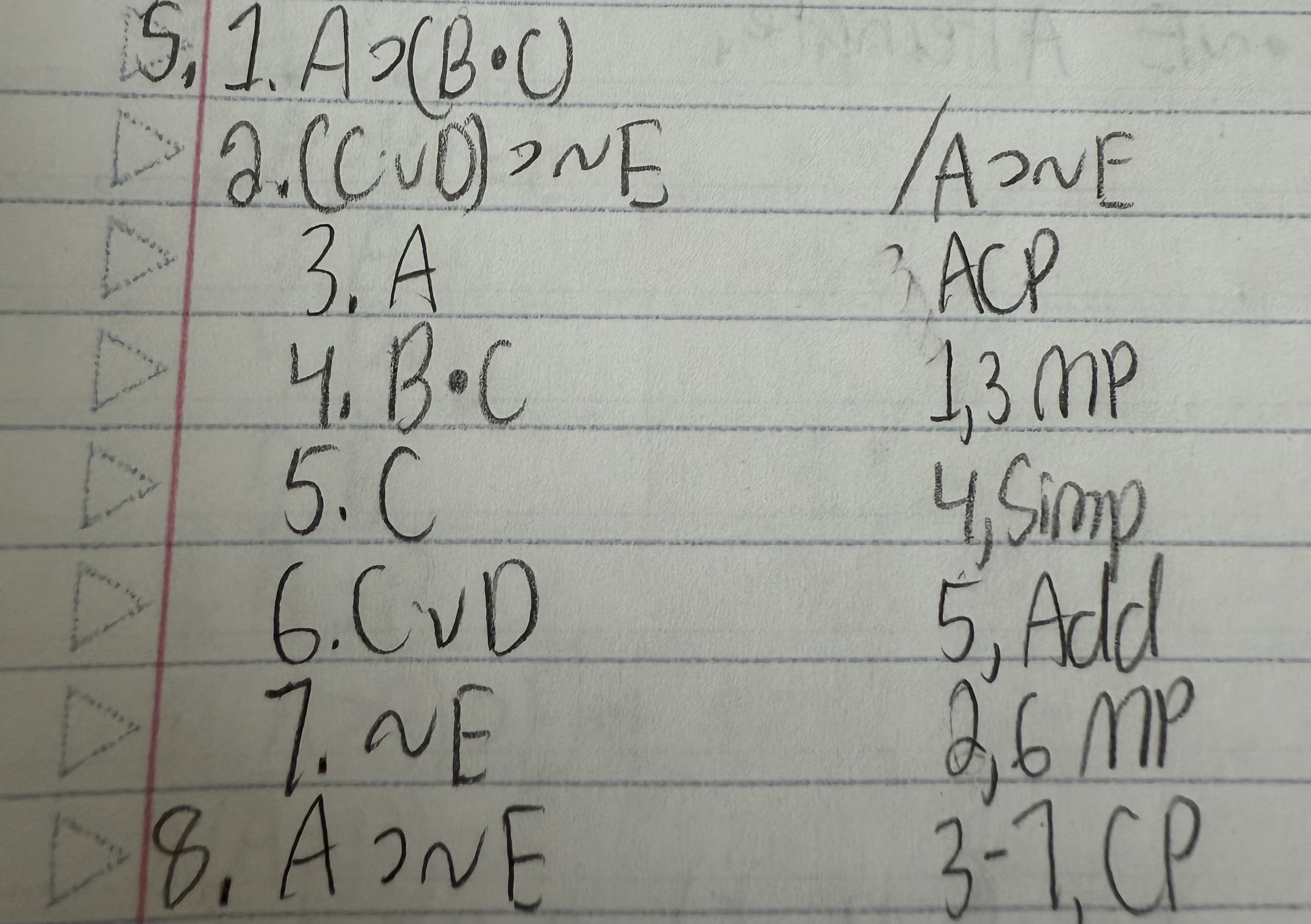
Use a conditional proof for the argument below:

1. A ⊃ (B ● C)

2. (C ∨ D) ⊃ ∼E                        /A ⊃∼E

Use a conditional proof for the argument below:

1. P ⊃ Q

2. (P ● Q) ⊃ ∼R /P ⊃ ∼R

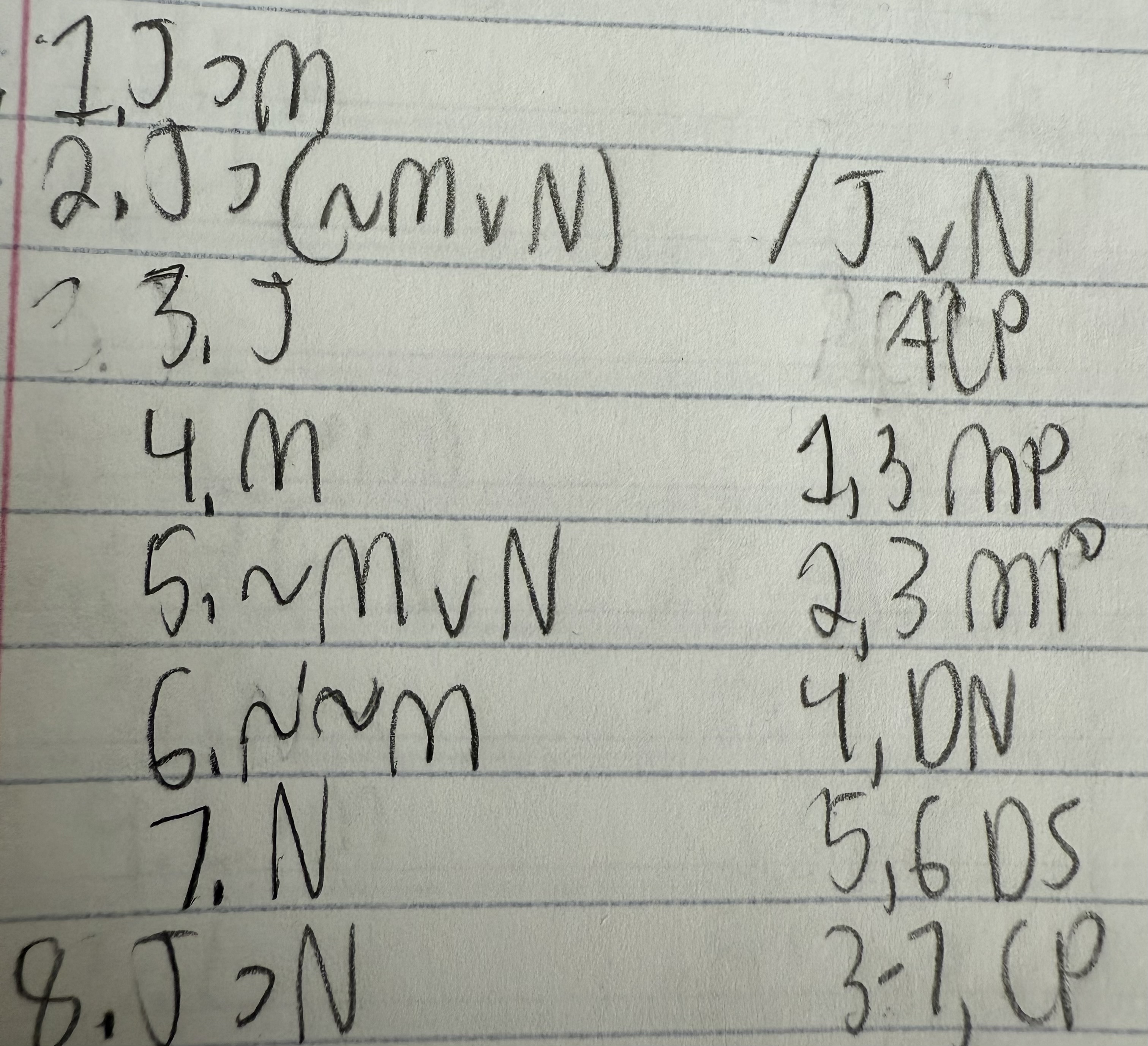
Use a conditional proof for the argument below:

1. J ⊃ M

2. J ⊃ (∼M ∨ N)           /J ⊃ N

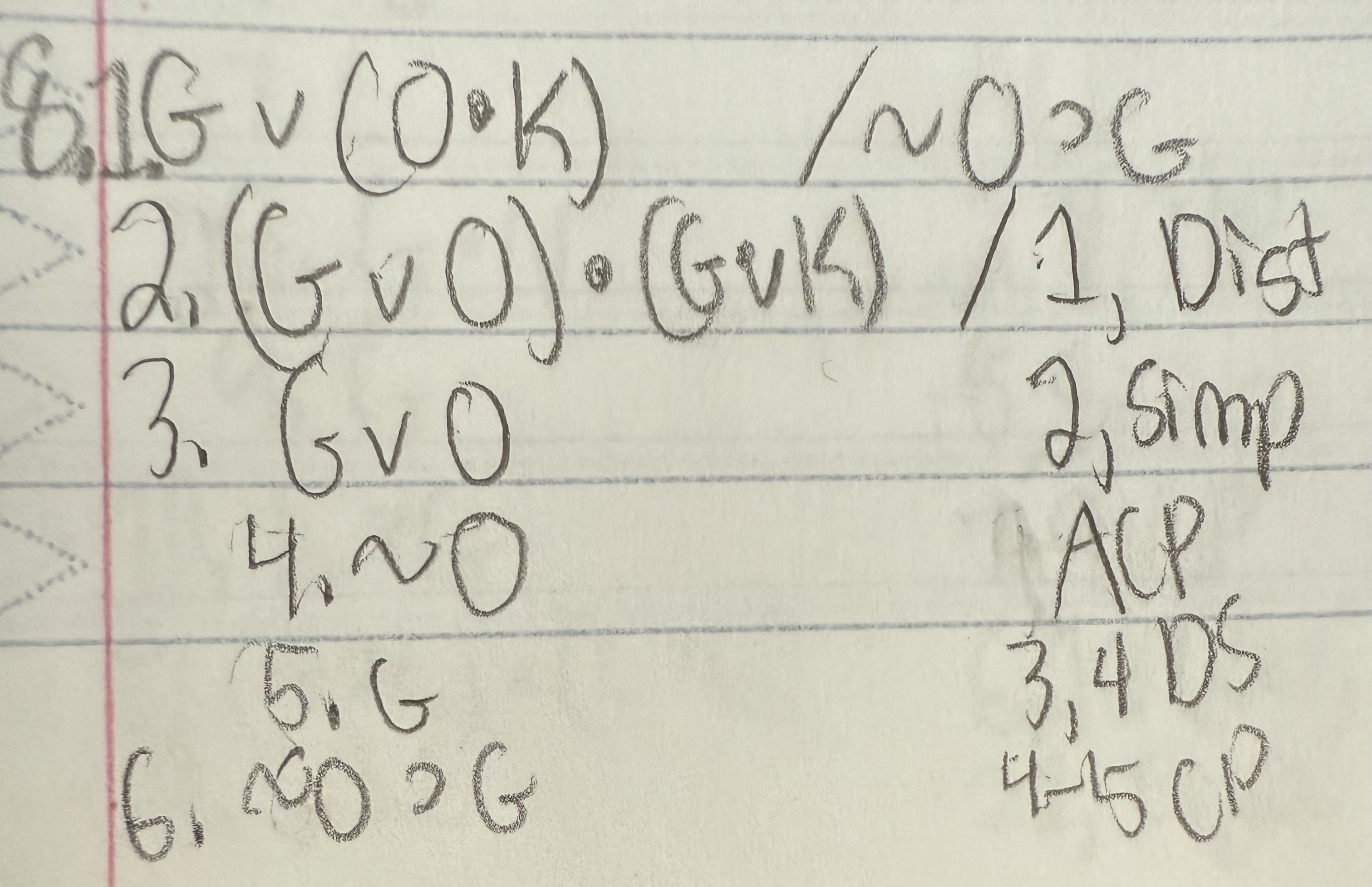
Use a conditional proof for the argument below:

Hint: remember that a conditional proof does not have to be started immediately.

1. G ∨ (O ● K)               /∼O ⊃ G

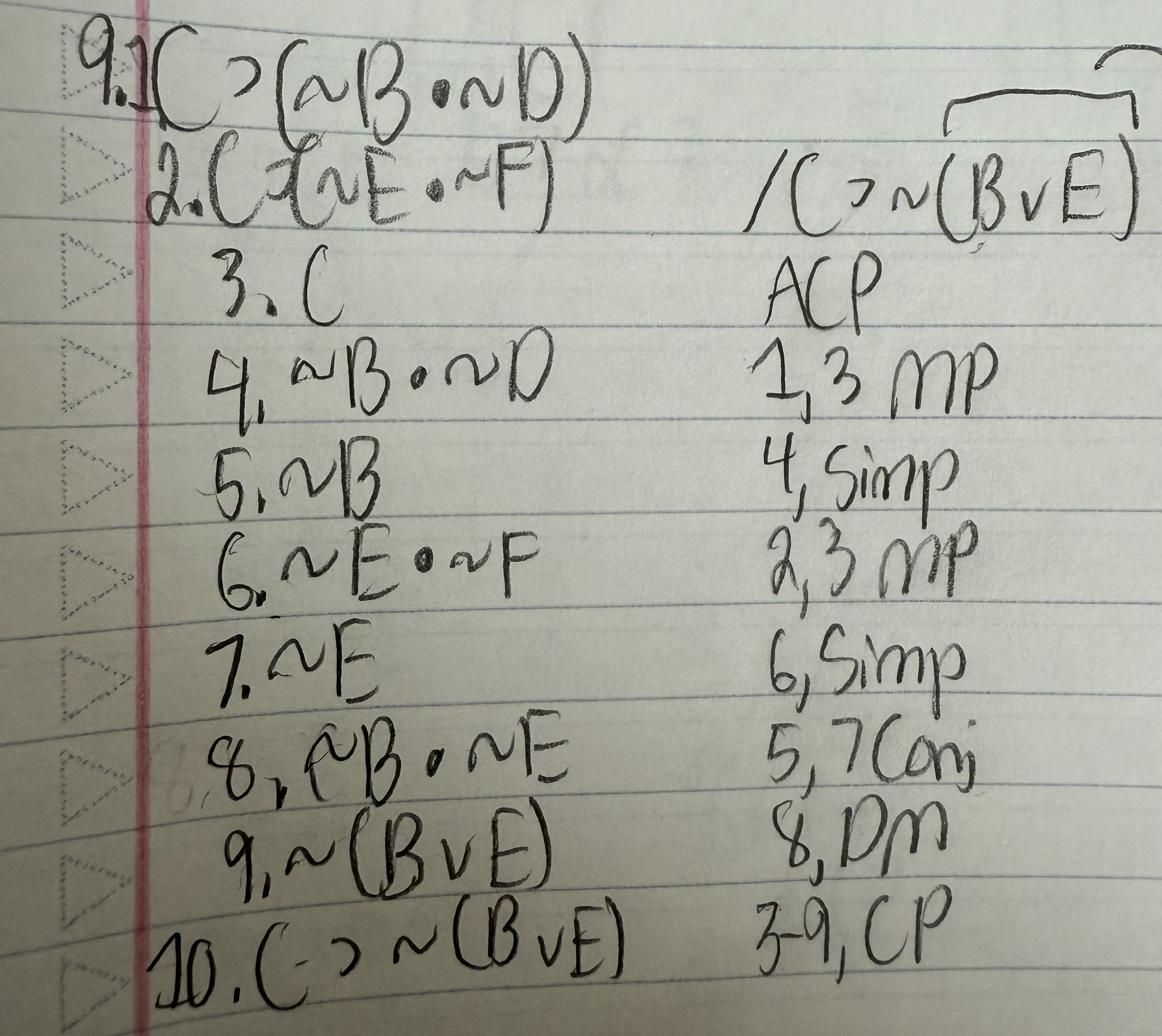
Use a conditional proof for the argument below:

1. C ⊃ (∼B ● ∼D)

2. C ⊃ (∼E ● ∼F)                 /C ⊃ ∼(B ∨ E)

Use a conditional proof for the argument below:

1. ∼P ∨ (Q ● R)

2. Q ⊃ L                     /P ⊃ (R ● L)

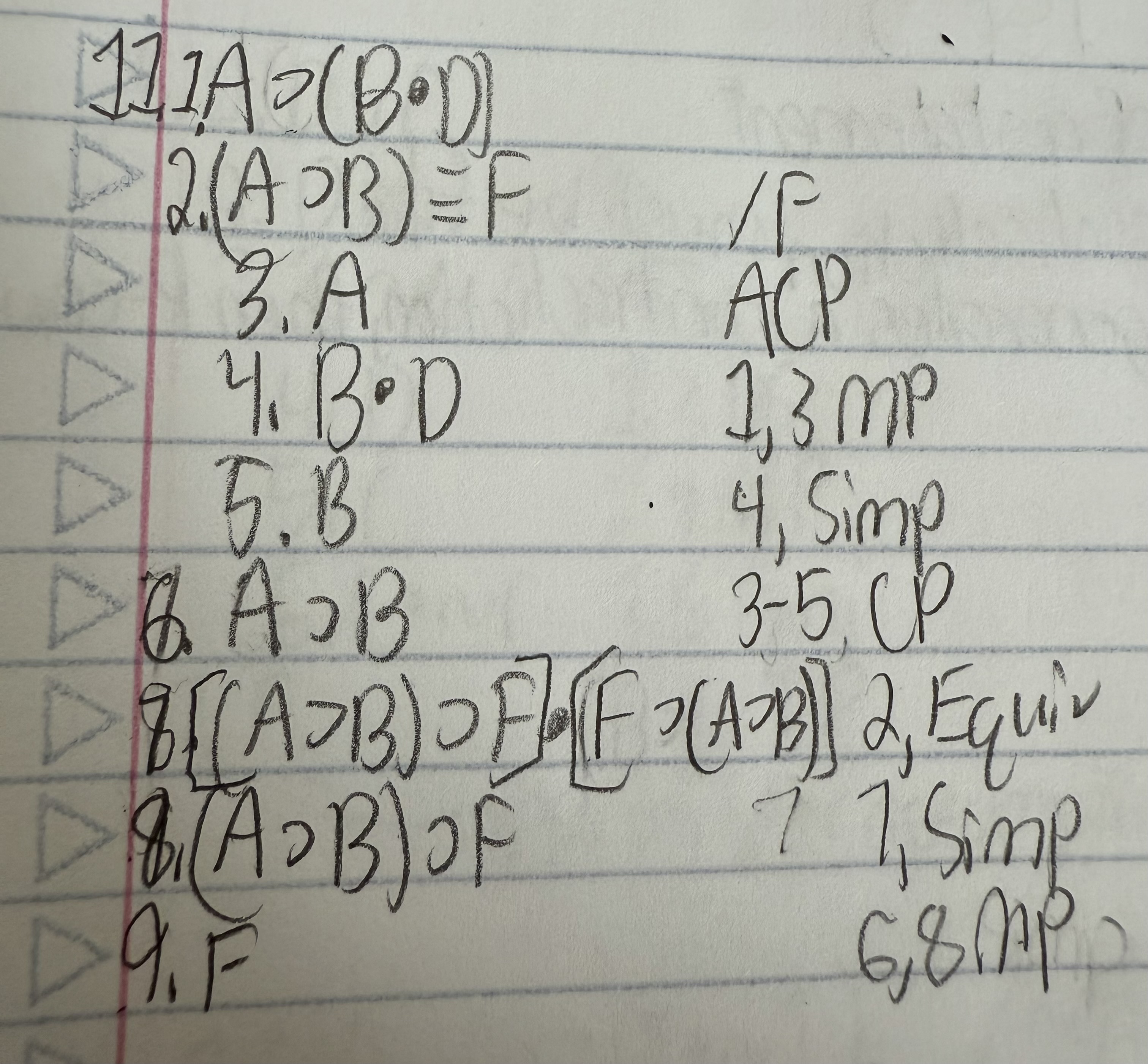
Use a conditional proof for the argument below:

1. A ⊃ (B ● D)

2. (A ⊃ B) ≡ F            /F

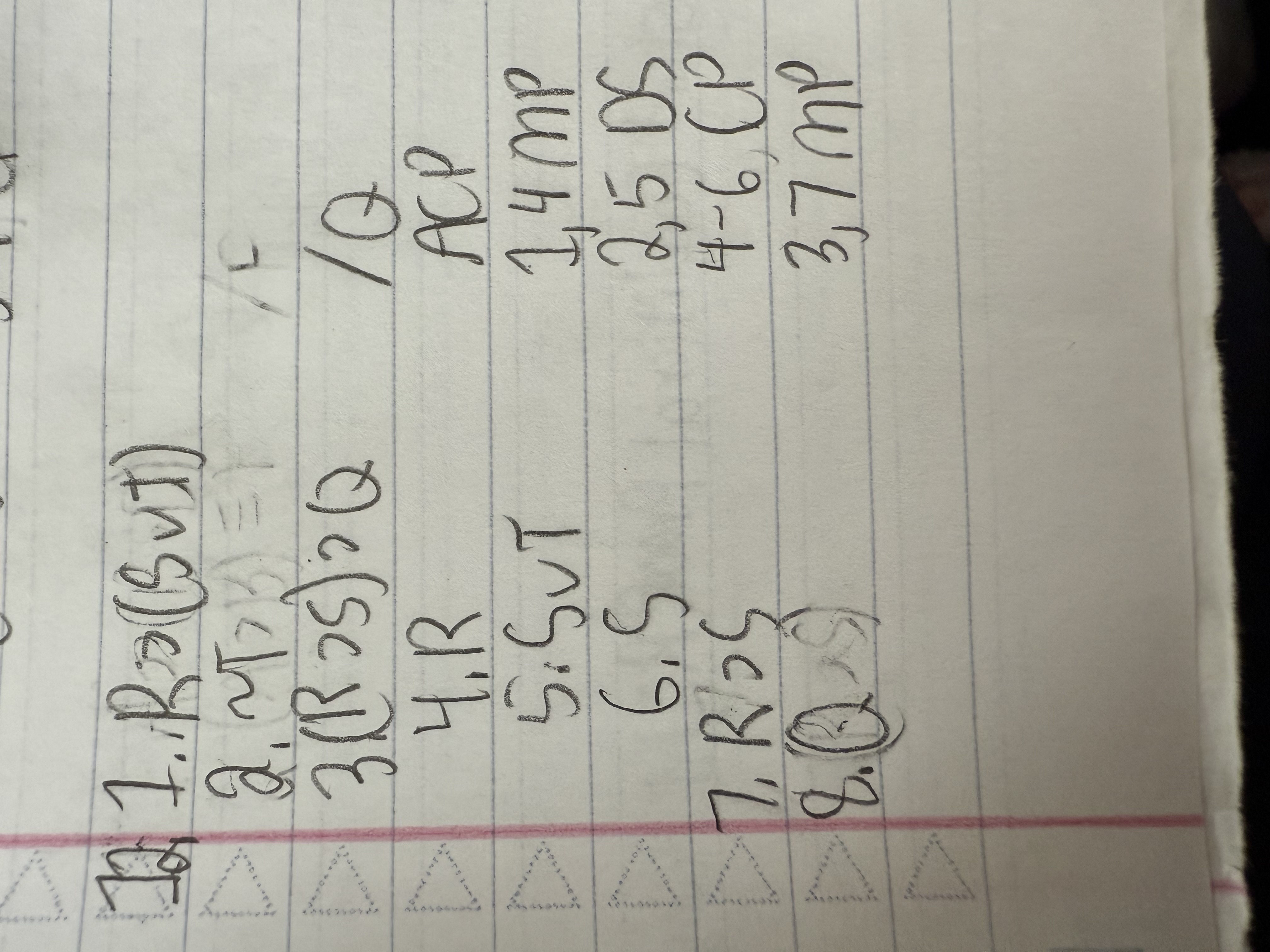
Use a conditional proof for the argument below:

1. R ⊃ (S ∨ T)

2. ∼T

3. (R ⊃ S) ⊃ Q          /Q

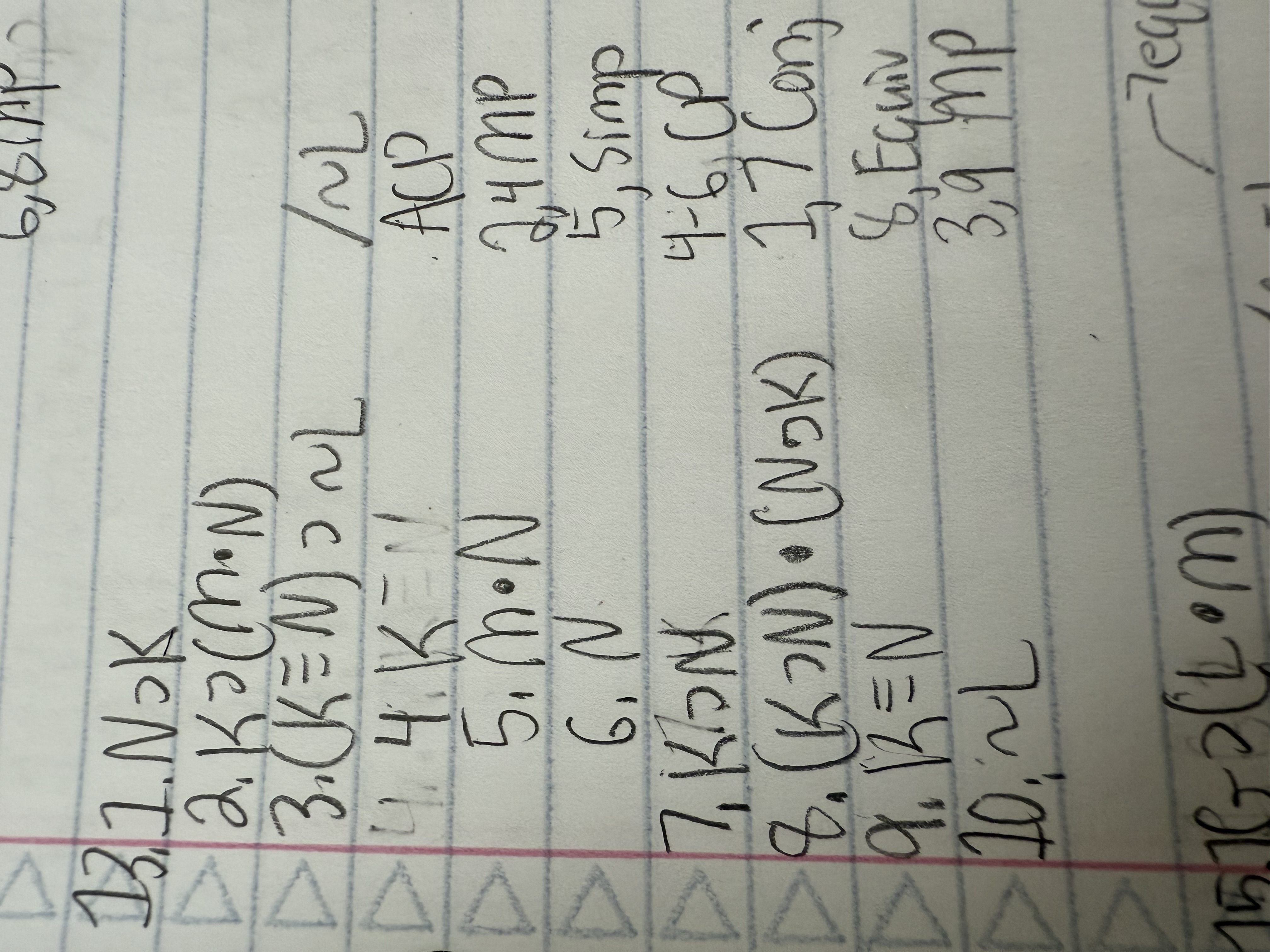
Use a conditional proof for the argument below:

1. N ⊃ K

2. K ⊃ (M ● N)

3. (K ≡ N) ⊃ ∼L          /∼L

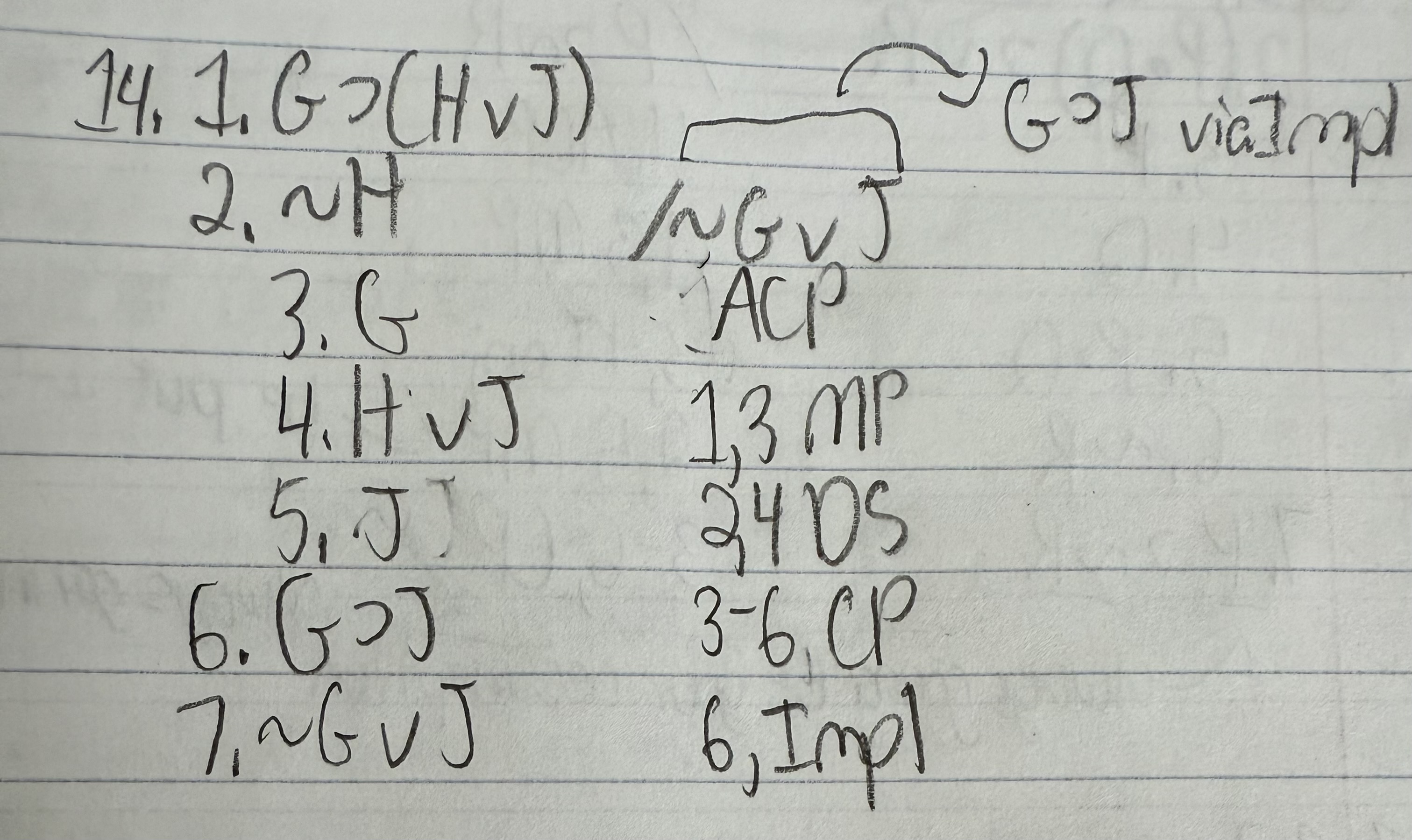
I think this is the answer, but we didn’t actually do this in class, so I don’t know!

Use a conditional proof for the argument below:

Hint: what is the conclusion equivalent to by implication?

1. G ⊃ (H ∨ J)

2. ∼H                /∼G ∨ J

Use a conditional proof for the argument below:

Hint: what is G  L equivalent to by the conjuctive form of the equivalence rule?

1. G ⊃ (L ● M)

2. L ⊃ (G ● N)          /G ≡ L