stat: t-toetsen

wat zijn t-toetsen?

We beschouwen niet meer dat we  kennen, want onrealistisch

• Oplossing gebruiken van s (standaardafwijking v steekproef), enkel als n groot is.

• T-toetsen gebruiken ipv z-toetsen

one sample t-test

= 1 steekproef

We gebruiken nu niet meer tabel A (= z-toetsen), maar tabel D (= t-toetsen)

Formule:

• Standaard error (SE): s/|n

• Vrijheidsgraden (k): bepaald door s ~ n-1 wordt gebruikt niet n (zie H1)

  • T(k) = t-verdeling

  • Specifieke t-verdeling

Wanneer t-verdelingen gebruiken?

• Normale verdeling: symmetrisch, unimodaal en klokvormig

• Hoe groter k, hoe meer de t-verdeling de normaalverdeling nadert (dus: hoe meer kans op een normale verdeling -> zie H1)

• Spreiding/ variantie (s) is groter

Betrouwbaarheidsinterval ~ opp C

• Formule (zie extra)

• Foutmarge: t* s/ √n

• p-waarde: 1-C/2  (1 staartje)

• t*: bovenste p-kritieke waarde (rechts)

  • afhankelijk van betrouwbaarheidsniveau: 68-95-99,7-regel

  • afhankelijk van # vrijheidsgraden (k)

fasen

• Hypotheses stellen

  • H₀ : µ = µ₀

  • Ha: µ <> µ₀ -> eenzijdig of tweezijdig

• bepalen ~ hier: 0,05

• Formules toepassen

• Kijken in tabel D -> p-waarde

  • p-waarde > alpha : niet significant

  • p-waarde </= alpha : significant

  • Bij gebruiken v betrouwbaarheidsinterval: kijken ligt het erin of niet?

    • Ligt er niet tussen → dan Ha

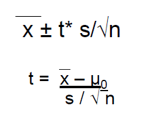
paired sample t-test

= 2 herhaalde metingen bij dezelfde steekproef

• Dezelfde metingen op verschillende momenten (pre en post)

• Met 2 analoge instrumenten (~ instrumenten dat hetzelfde meten)

Bedoeling

• je gaat een gemiddelde nemen van de pre-test en post-test. En dan zien is er een verschil/ effect tussen de 2. (geen effect, dan is het verschil = 0)

fasen

• Hypotheses stellen

  • H₀ : µ = µ₀

  • Ha: µ <> µ₀ -> eenzijdig of tweezijdig

• bepalen ~ hier: 0,05

• Formules toepassen

• Kijken in tabel D -> p-waarde

  • p-waarde > alpha : niet significant

  • p-waarde </= alpha : significant

  • Bij gebruiken v betrouwbaarheidsinterval: kijken ligt het erin of niet?

    • Ligt er niet tussen → dan Ha

robuusdheid van t-procedure (sample en paired)

= als kansberekeningen in toets ongevoelig zijn voor afwijkingen en gemaakte veronderstellingen

• Zeer robuust tov niet-normaliteit, maar niet robuust tov uitbijters (x en s zijn niet resistent)

• < 15pp: enkel bij normale verdeling + geen uitbijters

• >/= 15pp: bij normale verdeling (kan een klein beetje afwijken) + geen uitbijterq

• >/= 40pp: t-toetsen mag altijd gebruikt worden

independent sample t-test

wanneer gebruiken?

• Between design: 2 onafhankelijke groepen (bv. experimenteel en controlegroep)

  • Verschil tussen 2 steekproeven

• Bedoeling: gemiddelde in beide groepen bekijken en vergelijken. Beide steekproeven komen uit dezelfde populatie (Bv. rokers vs niet rokers of jongens vs meisjes)

formule

• Betrouwbaarheidsinterval ~zit 0 tussen het interval?

• # vrijheidsgraden: kleinste v n₁ -1 of n₂ -1

levence test

• variantietest ~ kijken of de variantie hetzelfde is bij beide groepen of niet

• F-toets voor het bepalen van homogeniteit/ gelijkheid van de varianties. Bekijken op = 0,01

  • Niet significant: equal variance assumed

  • Significant: equal variance not assumed

• Waarom 0,01 gebruiken? F-toets is zeer weinig robuust voor niet-normaliteit waardoor die snel in de 5% voorkomt. Men moet veel strenger zijn

equal variance assumed

• als de 2 steekproeven/ populaties dezelfde standaardafwijking hebben. (dezelfde variantie)

• Gevolg: men gebruikt formule van pooled variance

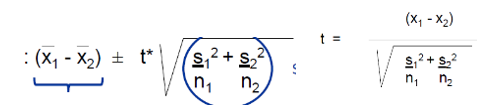
robuustheid independent sample t-test

• Independent sample t-test is robuuster dan one/ paired sample t-test

• T-toets is daar altijd nauwkeuriger