MM - Chapter 5: Basics of Digital Audio (copy)

what is sound?

Geluid is een golfverschijnsel zoals licht, maar macroskopisch → het gaat over luchtmoleculen die samengedrukt en uitgebreid worden door een fysiek apparaat.

• vb: een luidspreker beweegt heen en weer en maakt een longitudinale drukgolf die wij als geluid waarnemen.

• omdat geluid een drukgolf is, heeft het continue waarden (niet gedigitaliseerd).

Ondanks dat drukgolven longitudinaal zijn, vertonen ze gewone golfgedragingen zoals:

• reflectie (weerkaatsing)

• refractie (hoekverandering bij overgang naar een medium met andere dichtheid)

• diffractie (afbuigen rond een obstakel)

meten → de druk in een bepaalde locatie meten → transducer om de druk naar spanning om te zetten

Om een digitale versie van geluidsgolven te gebruiken, moeten we gedigitaliseerde representaties van audio maken.

Signalen kunnen worden opgesplitst in een som van sinusoïden → gewogen sinussen kunnen samen een complex signaal vormen.

pitch / fundamental frequence / overtones

pitch / fundamental frequence / overtones

• pitch: relatief, hoe een geluid klinkt, bepaald door de freq [relatief]

• fundamental frequentie: toon hoogte, de laagste frequentie component → bepaalt de pitch → partials [absolute measure]

• harmonische overtones: klankkleur, veelvouden van de fundamentele frequentie, geven kleur / karakter aan geluid → partials

• Noot A boven centrale C = vastgelegd op 440 Hz.

Octaven

• Eén octaaf hoger = frequentie verdubbeld.

• Voorbeeld: A4 (440 Hz) → A5 (880 Hz).

Complexe klanken

• Niet-gehele veelvouden → niet-A-noten → complexere, rijkere klank.

Bespreek digitization of sound. Wat betekenen sampling en quantization?

Digitalisering betekent: omzetten naar een stroom getallen, bij voorkeur gehele getallen voor efficiëntie.

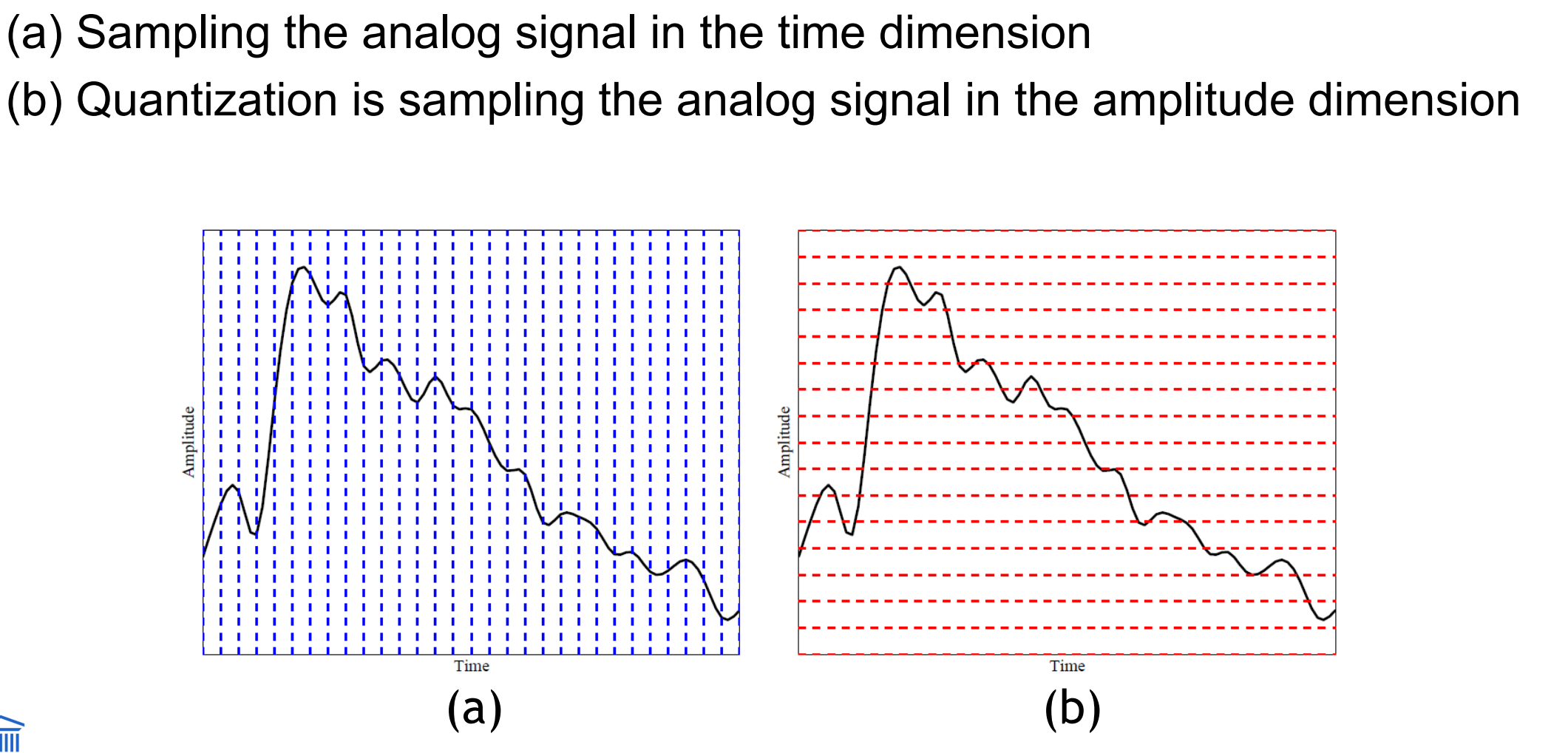
Geluid heeft een 1-dimensionale aard (amplitude hangt af van tijd).

Om te digitaliseren moet het signaal gesampled worden in elke dimensie: in tijd en in amplitude.

• Sampling = meten van de grootheid waarin we geïnteresseerd zijn, meestal op gelijkmatig verdeelde intervallen.

• Eerste soort sampling = alleen meten op gelijkmatig verdeelde tijdsintervallen → heet gewoon sampling.

  • De snelheid waarmee dit gebeurt = de samplingfrequentie.

  • Voor audio typisch: sampling rates van 8 kHz (8000 samples/sec) tot 48 kHz.

  • Deze range wordt bepaald door het Nyquist-theorema (later besproken).

kwantisatie: sampling in de aplitude / spannings-dimensie

Om te beslissen hoe we audiodata digitaliseren, moeten we antwoorden op:

• Wat is de sampling rate?

• Hoe fijn wordt de data gekwantiseerd, en is de kwantisatie uniform?

• Hoe wordt audiodata geformatteerd en/of gecomprimeerd (bestandstype)?

Nyquist theorem

• voorbeeld

• uitleg

• nog iets …

• aliasing uitleggen

Het Nyquist-theorema stelt hoe vaak we in de tijd moeten samplen om het originele geluid te kunnen reconstrueren.

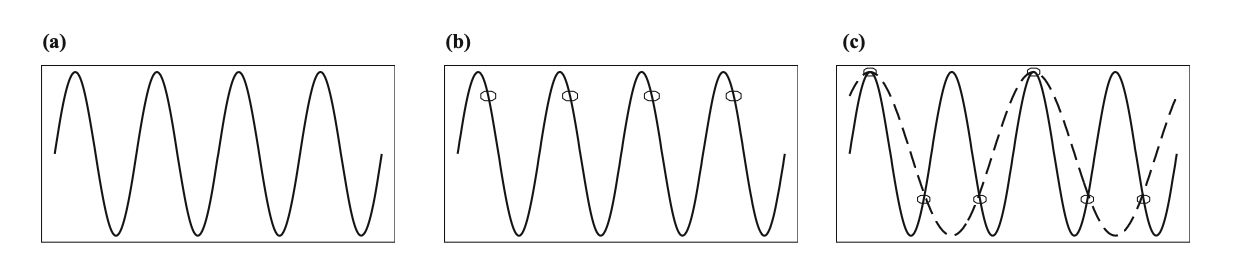
• a = enkele sinusgolf

  • zuiver frequentie signaal → elektronische instrumenten

• b = sampling rate = werkelijke frequentie

  • vals signaal → constante met nul freq

• c = sampling 1.5 * f

  • alias → frequentie lager dan de juiste

  • bij 1.5 → helft van de juiste

=> sampling rate van 2*fmax

• Dit heet de Nyquist-snelheid (Nyquist rate).

Nyquist-theorema: als een signaal bandbeperkt (bandlimited) is, d.w.z. er is een ondergrens f1 en een bovengrens f2 van frequentiecomponenten in het signaal, dan moet de sampling rate minstens 2(f2 – f1) zijn.

Nyquist-frequentie: de helft van de Nyquist-snelheid.

folding: f > fnyquist → gevouwen onder nyquist → aliasing

• Aangezien het onmogelijk is frequenties boven de Nyquist-frequentie te reconstrueren, hebben de meeste systemen een anti-aliasingfilter dat de frequentie-inhoud beperkt tot een bereik op of onder de Nyquist-frequentie.

De relatie tussen de samplingfrequentie, de werkelijke frequentie en de aliasfrequentie is als volgt:
f_alias = f_sampling – f_true, voor f_true < f_sampling < 2 × f_true.

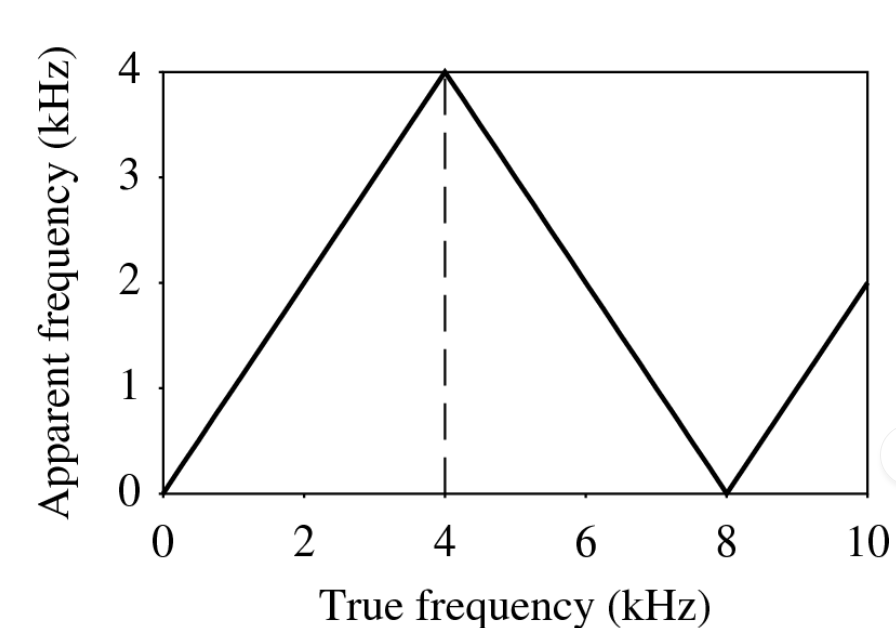
wat is apparent frequency

= de laagste frequentie van een sinusgolf die exact dezelfde samples heeft als de inputsinusgolf.

De figuur toont de relatie tussen de schijnbare frequentie en de inputfrequentie: vouwen (folding) van een sinusgolf die gesampled is aan 8 kHz. De vouwfrequentie (folding frequency), weergegeven als stippellijn, is 4 kHz.

Shannon’s sampling theorem

if a signal xa(t) is bandlimited with Xa(w) = 0 for |w| > wm, then xa(t) is uniquely determined by its samples provided that ws >= 2wm. The original signal may then be completely recovered by passing xs(t) through an ideal low-pass filter.

aka

Als een signaal bandbeperkt is tot ω_m, dan kan het volledig en uniek gereconstrueerd worden uit zijn samples als er gesampled wordt met minstens ω_s≥2ω_m, via een ideale low-pass filter.

• the frequency is ws/2 is called the Nyquist frequency

• if the condition is not satisfied, aliasing distorion occurs

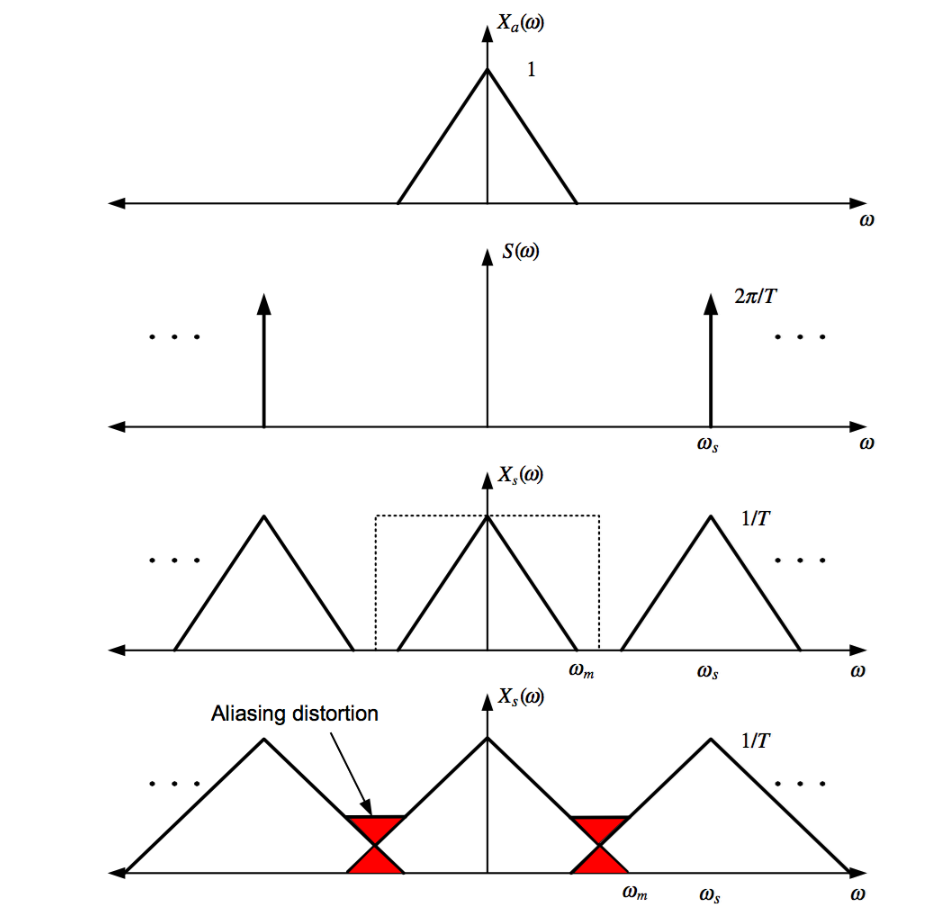
Deze figuur toont Shannon’s sampling theorem:

• Bovenste grafiek: het originele analoge signaal Xₐ(ω) met bandlimiet ωₘ.

• Tweede grafiek: het sampling spectrum S(ω), met pulsen op veelvouden van de samplefrequentie ωₛ = 2π/T.

• Derde grafiek: het gesamplede spectrum Xₛ(ω), een herhaling (replica) van het originele spectrum rond veelvouden van ωₛ.

→ Als ωₛ > 2ωₘ (dus ≥ Nyquist rate), blijven de replica’s netjes gescheiden en kan je het origineel perfect reconstrueren.

• Onderste grafiek: als ωₛ ≤ 2ωₘ, overlappen de replica’s → aliasing (rood aangeduid), wat onherstelbare vervorming geeft.

Kort: om aliasing te vermijden, moet je minstens dubbel zo snel samplen als de hoogste frequentie in het signaal.

Signal to noise ratio (SNR)

De verhouding van de kracht van het juiste signaal en de ruis wordt de signaal-ruisverhouding (SNR) genoemd — een maat voor de kwaliteit van het signaal.

De SNR wordt meestal gemeten in decibel (dB), waarbij 1 dB een tiende van een bel is. De SNR-waarde, in eenheid van dB, wordt gedefinieerd in termen van logaritmen met grondtal 10 van de kwadraten van spanningen, als volgt::

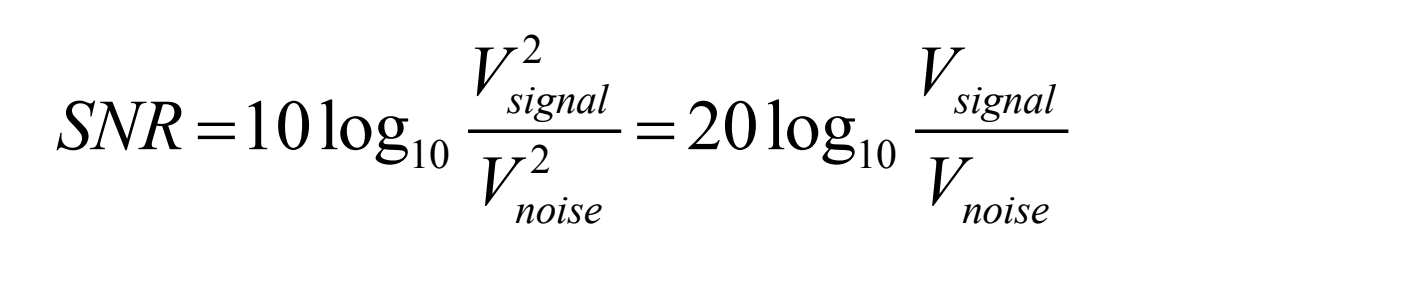
De gebruikelijke geluidsniveaus die we om ons heen horen, worden beschreven in termen van decibels, als een verhouding ten opzichte van het stilste geluid dat we kunnen horen.

Quantization error en Signal to quantization noise ratio (SQNR)

Naast alle ruis die mogelijk al aanwezig was in het originele analoge signaal, is er ook een extra fout door kwantisatie.

• Als spanningen eigenlijk tussen 0 en 1 liggen maar we slechts 8 bits hebben om waarden op te slaan, dwingen we alle continue spanningswaarden effectief in slechts 256 verschillende waarden.

• Dit introduceert een afrondingsfout. Het is niet echt “ruis”, maar wordt toch kwantisatieruis (of kwantisatiefout) genoemd.

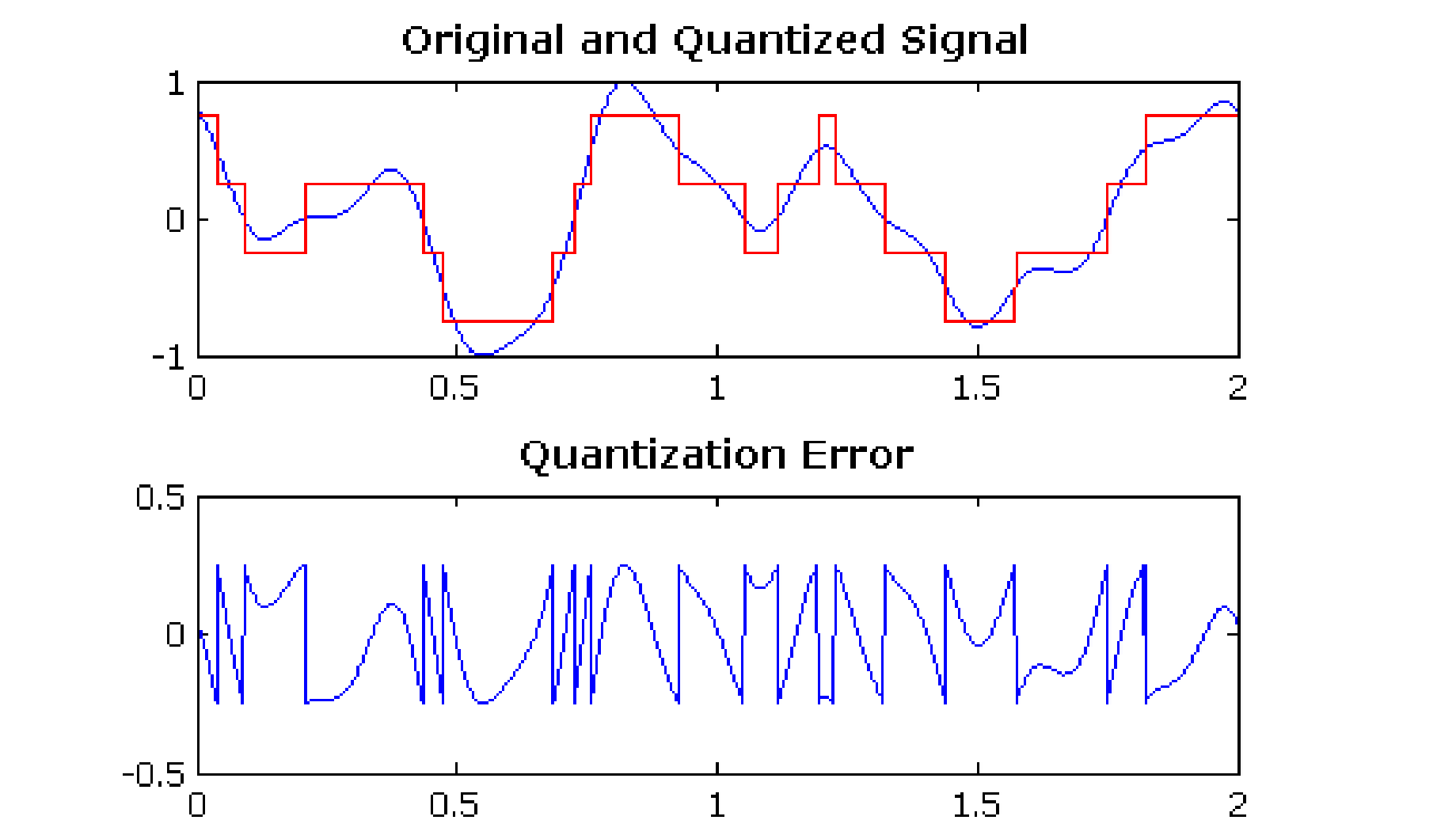
De kwaliteit van de kwantisatie wordt gekarakteriseerd door de signaal-tot-kwantisatieruisverhouding (SQNR).

• Kwantisatieruis: het verschil tussen de werkelijke waarde van het analoge signaal, voor het specifieke samplingmoment, en de dichtstbijzijnde kwantisatie-intervalwaarde.

• In het uiterste geval kan deze fout maximaal zo groot zijn als de helft van het interval.

linear and nonlinear quantization

Lineair formaat: samples worden meestal opgeslagen als uniform gekwantiseerde waarden

Niet-uniforme kwantisatie: fijnere niveaus instellen waar mensen het best horen

• Weber’s Wet zegt formeel: gelijk waargenomen verschillen zijn evenredig met absolute niveaus →
  ΔResponse ∝ ΔStimulus / Stimulus

• Oplossing door integratie (met integratieconstante C):
  r = k ln(s) + C

• Of herschreven (waar s₀ = laagste stimulusniveau dat respons geeft, r = 0 als s = s₀):
  r = k ln(s / s₀)

Niet-lineaire kwantisatie: eerst analoog signaal transformeren van ruwe s-ruimte naar theoretische r-ruimte, daarna uniform kwantiseren

• Voor audio: μ-law-encoding (of u-law)

• In Europa (telefonie): gelijkaardige regel, A-law

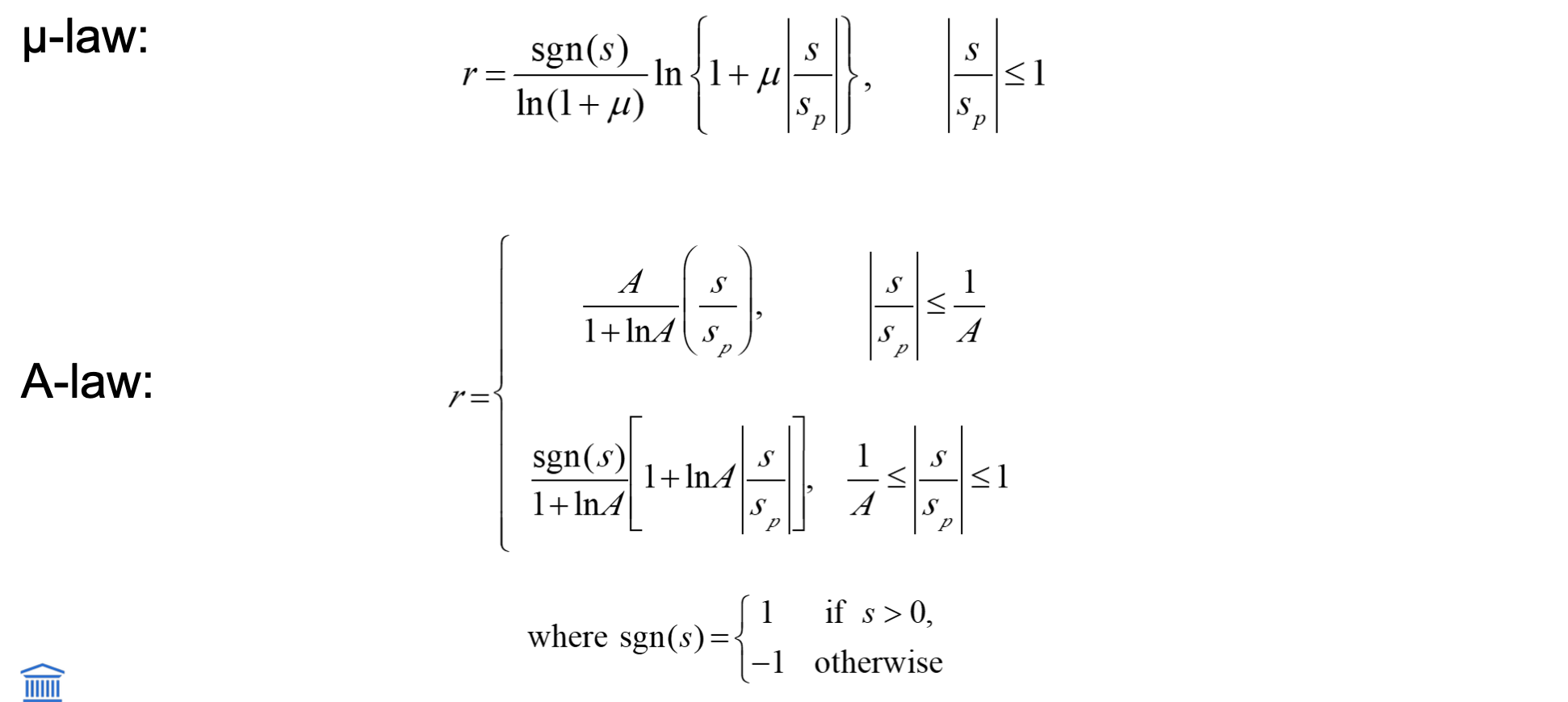
Stap-voor-stap:

• eerst normaliseren door signaal te delen door kleinste stimulus die een respons uitlokt → s/s0

• Dan pas je de logtransformatie toe → compressor

  • A/µ - law

  • Dit zet je signaal om naar de r-ruimte, waar de schaal past bij

  • menselijke perceptie

    • kleine veranderingen bij zachte signalen → groot

    • luide signalen → klein.

• Vervolgens kwantiseer je r uniform

  • dus je deelt r op in gelijke stappen, omdat je dankzij de transformatie al rekening hebt gehouden met de niet-lineaire gevoeligheid van het menselijk gehoor.

• ontvanger kant via expander de oorspronkelijke schaal herstellen

companing: compressing + expanding

Dus ja: eerst transformeren, dan uniform kwantiseren. Dat is hoe μ-law en A-law werken.mens → mu of A

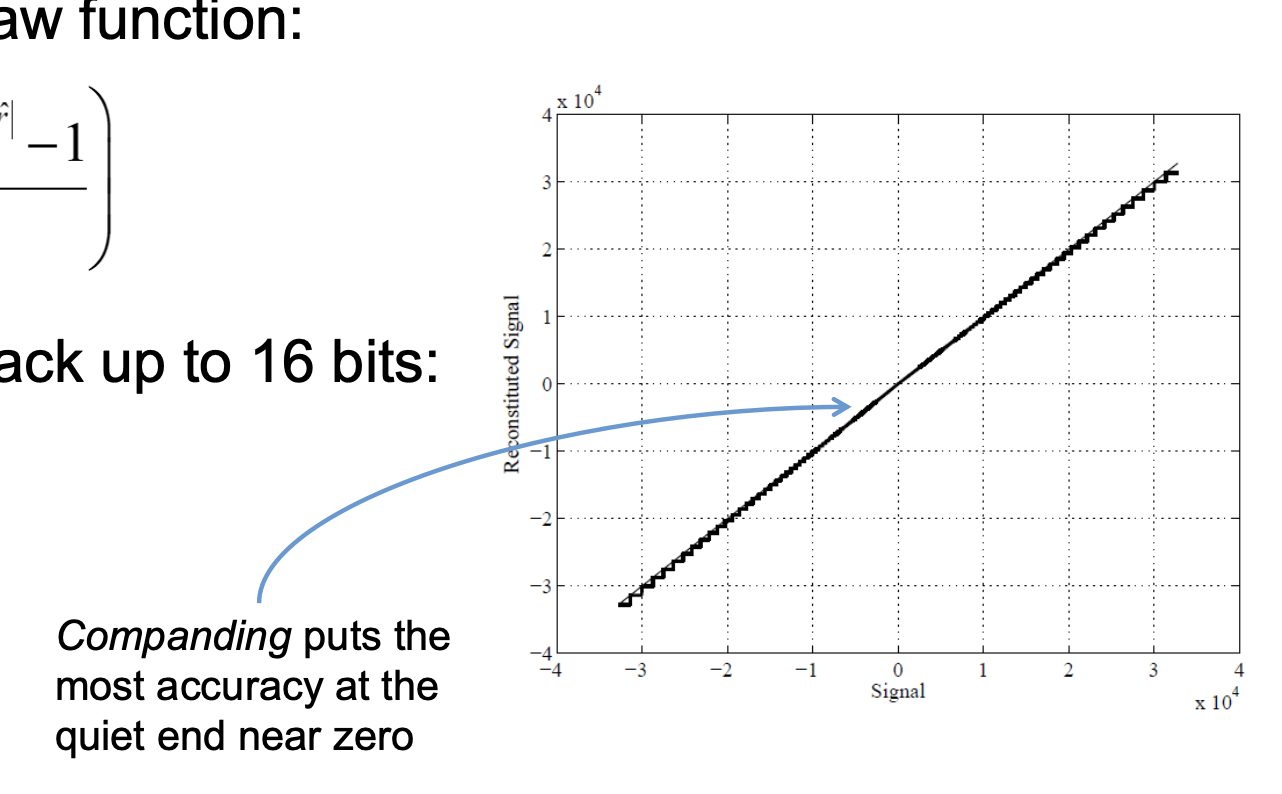
bit allocation in μ-law

In μ-law willen we de beschikbare bits inzetten waar de menselijke perceptie het meest gevoelig is voor kleine veranderingen.

• signaal met kleinere bitdiepte verzenden

• μ-law begint vaak met een bitdiepte van 16 bits, maar verzendt met slechts 8 bits.

• Aan de ontvangerzijde wordt het signaal weer uitgebreid naar 16 bits.

Stappen:

1. Begin met analoog signaal s, meestal in bereik [−2¹⁵, 2¹⁵−1] voor 16 bits.
   → Normaliseer naar bereik [−1, 1] door te delen door 2¹⁵.

2. Pas de μ-law transformatie toe met μ (bijvoorbeeld 255):
   → Zet s om naar r met logaritmische schaal (compressor).
   → Hierdoor krijgen zachte signalen meer detail, luide signalen minder, volgens menselijke gevoeligheid.

3. Reduceer bitdiepte:
   → Zet r om naar 8-bits sample met
   r̂ = sign(s) · floor(128 · r).

4. Transmissie:
   → Verzend enkel de 8-bits r̂, waardoor bits worden bespaard.

5. Aan de ontvangerzijde:
   → Normaliseer r̂ door te delen door 2⁷.
   → Pas inverse μ-law toe (expander) om oorspronkelijke schaal terug te halen.
   → Herstel zo een 16-bit signaal met redelijke kwaliteit.

Theorie uit het boek aangevuld:

• Dit proces heet companding (compressing + expanding).

• Oorspronkelijk analoog uitgevoerd, maar nu vaak volledig digitaal.

• Het werkt door eerst in de s-ruimte te transformeren naar de r-ruimte (via logaritmische compressie), daar uniform te kwantiseren, en bij ontvangst weer terug te transformeren.

audio filtering

Voor sampling en AD-conversie wordt het audiosignaal meestal gefilterd om ongewenste frequenties te verwijderen. Welke frequenties behouden blijven, hangt af van de toepassing:

• Voor spraak: meestal tussen 50 Hz en 10 kHz behouden, andere frequenties geblokkeerd met een bandpass-filter dat lagere en hogere frequenties wegfiltert.

• Voor muzieksignalen: typisch van ongeveer 20 Hz tot 20 kHz behouden.

Aan de DA-converterkant kunnen hoge frequenties opnieuw opduiken in de output:

• Door sampling en kwantisatie wordt het vloeiende inputsignaal vervangen door een reeks stepfuncties die alle mogelijke frequenties bevatten.

• Daarom gebruikt men aan de decoderzijde een low-pass-filter na het DA-circuit.

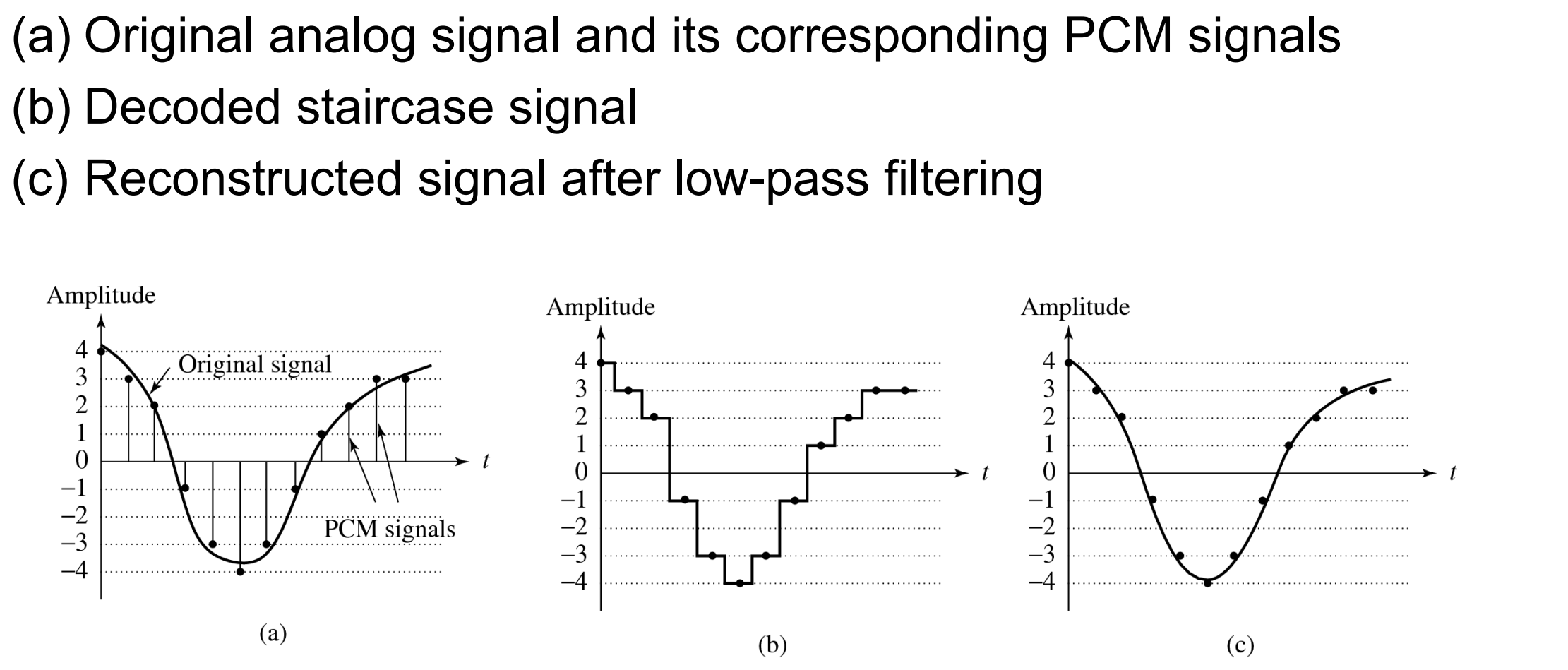
Figuur:
(a) Oorspronkelijk analoog signaal en bijhorende PCM-signalen
(b) Gedecodeerd trapjessignaal
(c) Gereconstrueerd signaal na low-pass-filtering

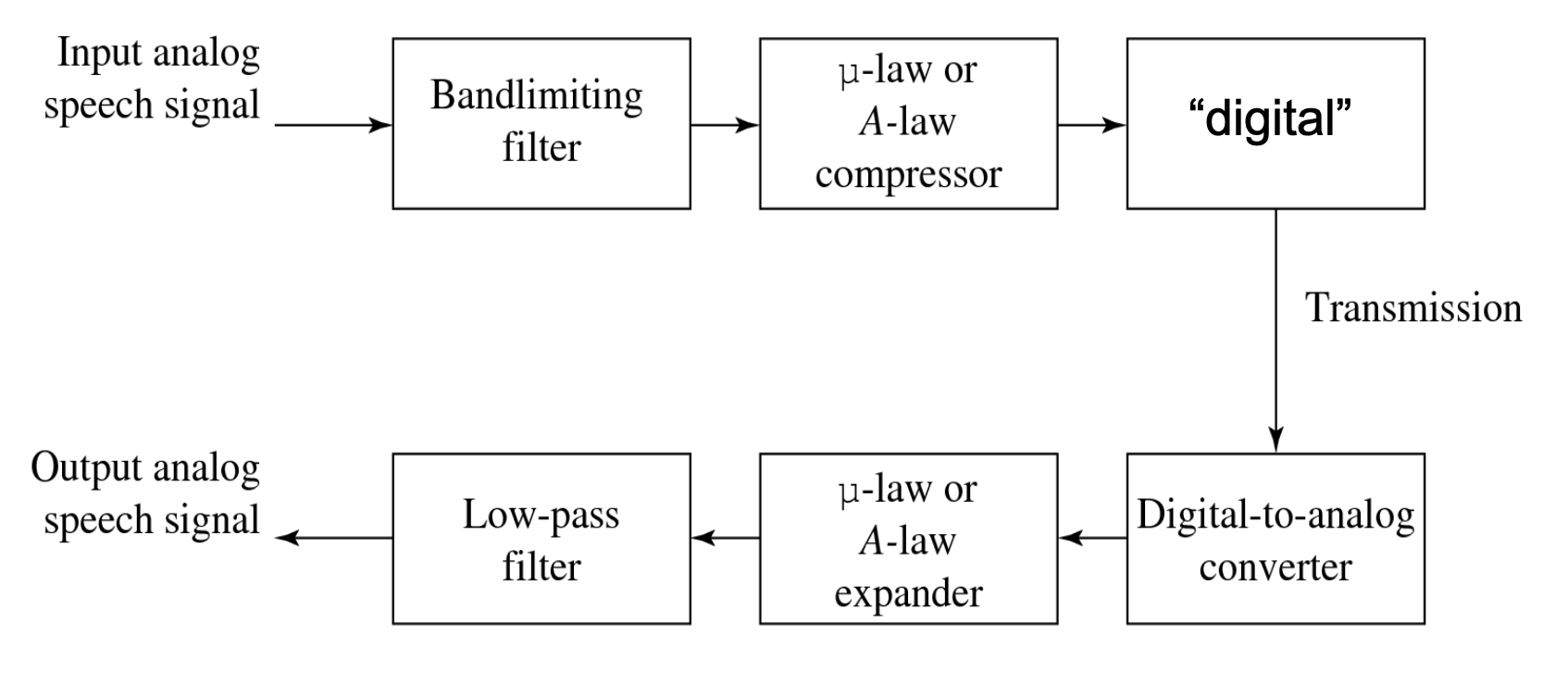
Digitization of sound volledig proces (figuur)

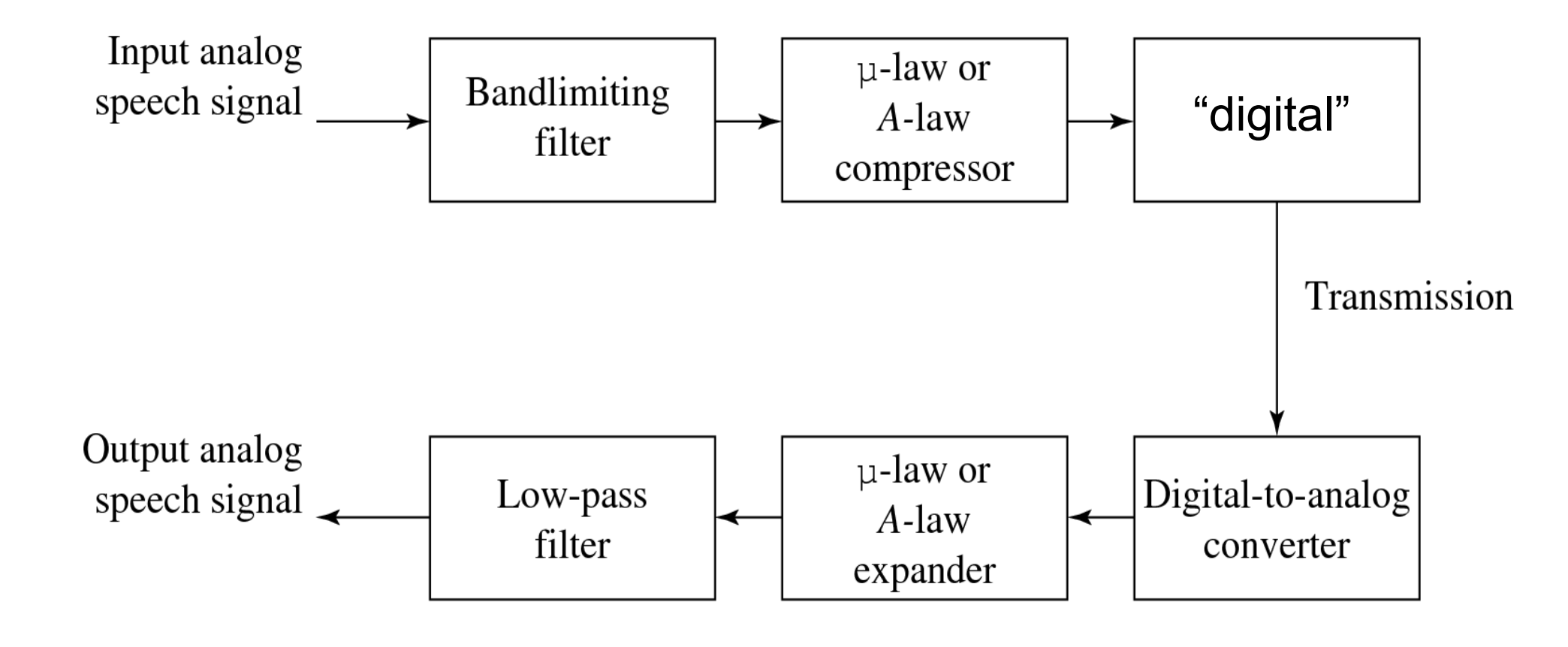
Toelichting bij figuur:

Bovenzijde (voor transmissie):

• Input analoog spraaksignaal gaat eerst door een bandlimiterend filter → ongewenste frequenties (te laag of te hoog) worden weggefilterd.

• Daarna wordt een μ-law of A-law compressor toegepast → logaritmische transformatie zodat zachte signalen fijn en luide signalen grof behandeld worden (past bij menselijke perceptie).

• Vervolgens wordt het signaal gedigitaliseerd (sampling + kwantisatie) en overgedragen.

Onderzijde (na transmissie):

• Digitaal signaal wordt eerst omgezet naar analoog via een digital-to-analog converter.

• Vervolgens herstelt de μ-law of A-law expander de oorspronkelijke schaal (inverse transformatie).

• Tot slot haalt een low-pass-filter de hoge frequenties weg die door de trapstructuur (sampling/kwantisatie) ontstaan zijn → gereconstrueerd, glad analoog uitgangssignaal.

Kort gezegd: dit schema toont het volledige compressie–transmissie–expansieproces (companding) dat we besproken hebben, inclusief filtering, transformatie en herstel.

audio quality vs data rate (kort)

om een digitaal audio signaal te transmitten → uncompressed data rate wordt groter naarmate meer bits gebruikt worden voor quantisatie

stereo verdubbeld meestal de bb

Synthetics sounds (2 approaches)

FM (Frequency Modulation)

• Usually, FM is carried out using a sinusoid argument to a sinusoid

Basisidee: geluid(golf) gegenereerd obv formules ipv sample waarden
We maken een signaal met een carrierfrequentie ωc en voegen een extra modulerende frequentie ωm toe.

Parameters voorbeeld (figuur 5.10d):

• ωc = 2, ωm = 4

• ϕm en ϕc (faseconstanten) zorgen voor tijdverschuivingen → interessantere klank.

Functie A(t) (envelope):

• tijdsafhankelijke functie die de algemene luidheid over tijd bepaalt.

• gebruikt om het geluid in en uit te faden.

• typisch patroon zoals bij gitaarsnaar: attack, decay, sustain, release.

Functie I(t):

• tijdsafhankelijke functie die harmonischen (“overtones”) creëert door het modulatiefrequentiebereik te veranderen.

  • klein I(t) → vooral lage frequenties hoorbaar.

  • groot I(t) → ook hoge frequenties hoorbaar.

Toepassing:
FM-synthese wordt gebruikt in goedkope geluidskaarten, maar ook in kaarten met backward compatibility.
Door de parameters van de generatiefunctie aan te passen, kan men veel verschillende klanken produceren.

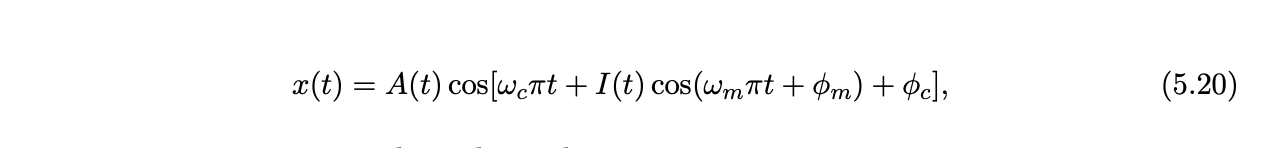
Wave Table-synthese

• Een nauwkeurigere manier om geluiden te genereren uit digitale signalen

• Ook simpelweg bekend als sampling

• Bij deze techniek worden de echte digitale samples van geluiden van echte instrumenten opgeslagen

• Omdat wave tables in het geheugen op de geluidskaart worden bewaard, kunnen ze door software gemanipuleerd worden zodat geluiden gecombineerd, bewerkt en verbeterd kunnen worden

Quantization and transformation of data (coding of audio)

1. uitleg (3)

2. verschillende stappen

codering = quantization + transofrmatie → opslaan / versturen

• voor audio:

  • µ-law: companding

  • algo: temporele redundantie benut

• Verschillen tussen het huidige en een vorig signaalpunt

  • verminderen grootte van de signaalwaarden

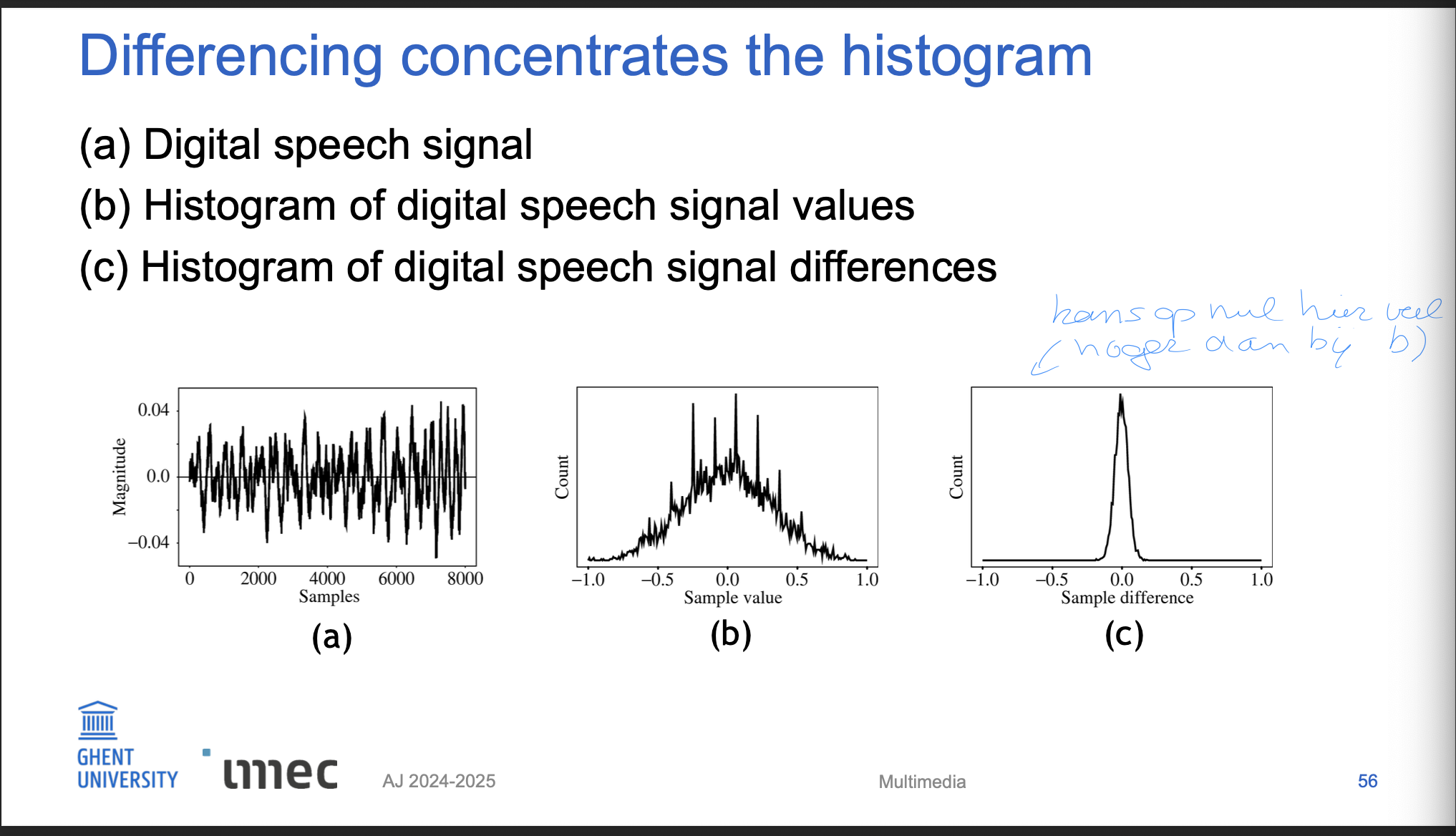
  • histogram verdeling concentreren in kleiner bereik

• variantie van waarden verkleinen

  • lossless compressiemethoden → bitstroom genereren met kortere bitlengtes voor waarschijnlijkere waarden

Elke compressiemethode heeft drie stappen:

1. Transformatie: De invoerdata wordt getransformeerd naar een nieuwe representatie die makkelijker of efficiënter te comprimeren is

2. Loss: Er kan informatie verloren gaan:

   1. kwantisatie is de belangrijkste ‘lossy’ stap

   2. beperkt aantal reconstructie niveaus, minder dan in originele

3. Entropiecodering: wijs een codewoord (vormt een binaire bitstroom) toe aan elke uitvoerwaarde of symbool (verliesloos proces); dit kan een vaste-lengtecode zijn of een variabele-lengtecode, zoals Huffman-codering (hoofdstuk 6)

In het algemeen heet gekwantiseerd sample-uitvoer voor audio PCM (Pulse Code Modulation)
De verschillenversie heet LPC (lossless) of DPCM (lossy, met kwantisatie); een simpele maar efficiënte variant heet DM
De adaptieve versie heet ADPCM

PCM voor spraak compressie

Hier is een kort overzicht:

Pulse Code Modulation (PCM)

• Basis: zet analoge signalen om naar digitale signalen via sampling en kwantisatie.

  

Processtappen:

1. Input analoog signaal → sampling → kwantisatie → digitaal signaal (PCM).

2. Tijdens transmissie kan bitreductie toegepast worden (bijv. met μ-law of A-law).

3. Aan de ontvangende kant: digitaal → analoog via DA-conversie + low-pass-filter voor gladde reconstructie.

Belangrijk:

• μ-law / A-law compressie: gebruikt om gevoeligheid voor kleine veranderingen te behouden én bitgebruik te verminderen.

• Low-pass-filter aan outputzijde verwijdert hoge frequenties die ontstaan door trapvormige reconstructie.

• Dit hele schema is de standaard voor telefoniesignalen en sluit aan bij datacommunicatieconcepten.

Differential coding of audio

• hoezo kan dit?

• iets te maken met codering?

Hier een korte en gestructureerde samenvatting:

Audioopslag met verschilcodering

• In plaats van simpel PCM gebruikt men vaak opslag die verschillen tussen opeenvolgende samples benut (kleinere getallen → minder bits nodig).

Temporal redundancy

• Tijdafhankelijke signalen tonen vaak consistentie → verschil tussen huidig en vorig sample (difference signal) geeft een histogram met piek rond nul.

• Voorbeeld:
   - Lineair rampsignaal met constante helling → vlak histogram.
   - Afgeleide (verschilsignaal) → spike in histogram op hellingswaarde.

Codering

• Door bit-string codewoorden toe te wijzen aan verschillen kunnen:
   - Korte codes gaan naar veelvoorkomende waarden.
   - Lange codes gaan naar zeldzame waarden.

Lossless predictive coding

• leg uit

• wat is het probleem + oplossing

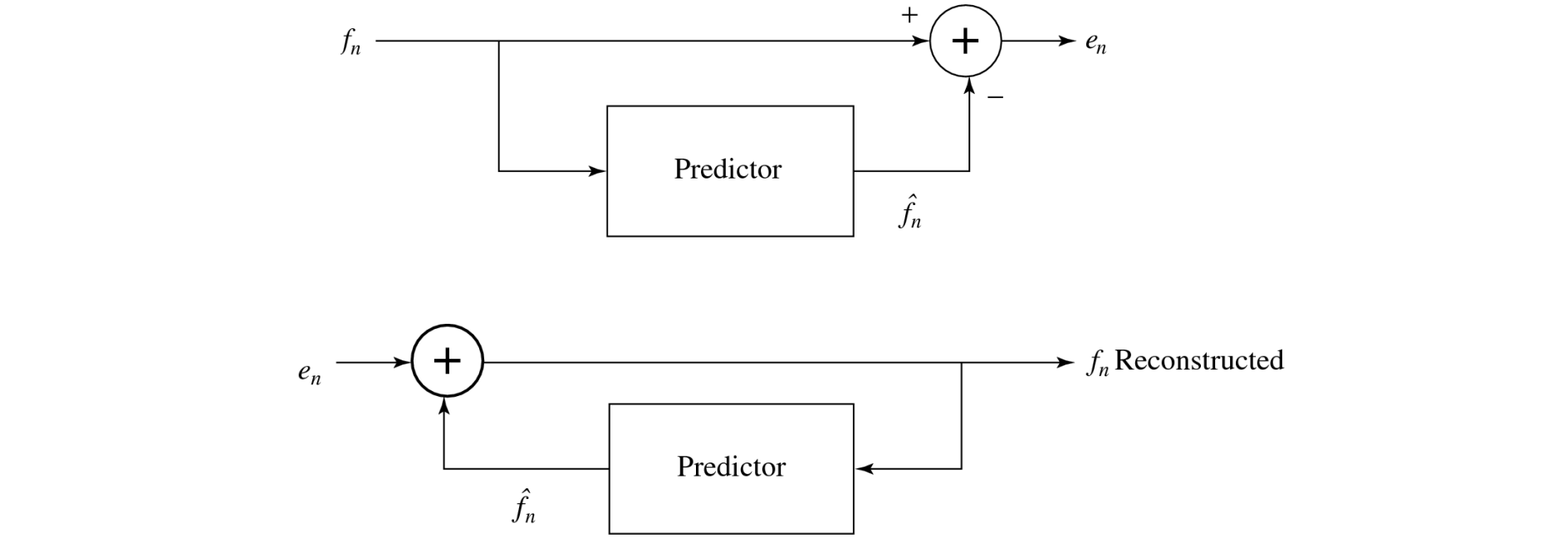
• schematic diagram (figuur!)

→ zorg daje ier ook “oef” op kan

Predictive coding → enkel verschillen doorsturen, niet het sample zelf

• Volgende sample voorspeld als huidig sample

• Verstuurd: verschil tussen vorige en volgende

Stappen: vinden van verschillen en deze doorsturen met PCM

• Note that differences of integers will be integers. Denote the integer input signal as the set of values fn. Then we predict values ˆfn as simply the previous value, and define the error en as the difference between the actual and the predicted signal:
  

  

• Verbetering: lineaire predictor function

  • kans dat een vorige fn-x een betere voorspelling is

  • → Voorspelling op basis van meerdere vorige waarden

    

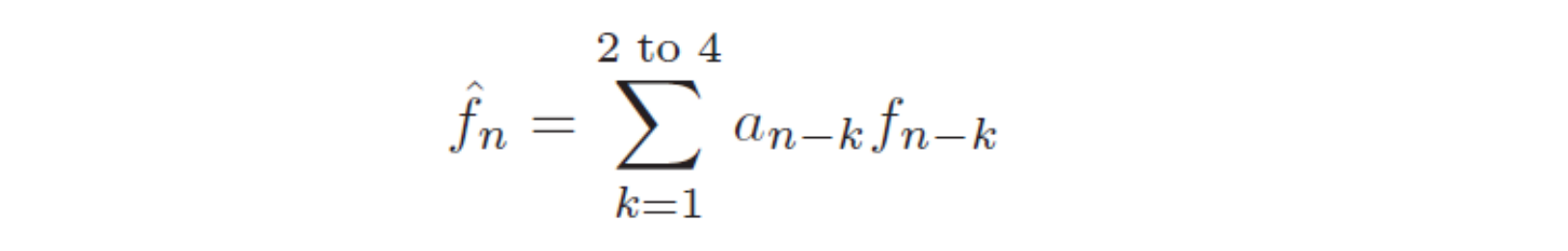
probleem

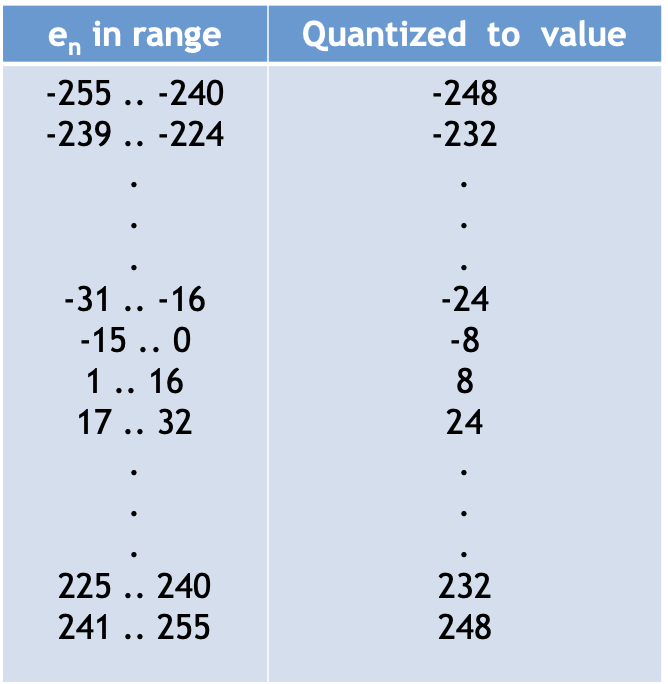
• integer sample values: [0, 255]

• verschillen: [-255, 255]

• dynamic range * 2 → dubbel zoveel bits nodig om de verschillen te sturen

oplossing

• 2 nieuwe codes: shift-up en shift-down → 32

• Voor deze (SU, SD) worden speciale codewaarden gereserveerd.

• We gebruiken codewoorden enkel voor een beperkte set signaalverschillen, bv. bereik [-15,16].

• Verschillen binnen dit bereik → direct coderen.

• Verschillen buiten dit bereik → gebruik SU/SD (Shift-Up / Shift-Down) in stappen, gevolgd door een waarde binnen [-15,16].

Voorbeeld:

• 100 verzenden → SU, SU, SU, 4
  → dus drie keer SU en dan 4

• 18 → SU, -14

Differential Pulse code modulation (DPCM)

• wat

• stappen

• schematic diagram (figuur!)

Differential PCM is exactly the same as Lossless Predictive Coding, except that it incorporates a quantizer step.

• One scheme for analytically determining the best set of quantizer steps, for a non-uniform quantizer, is the Lloyd-Max quantizer, which is based on a least-squares minimization of the error term.

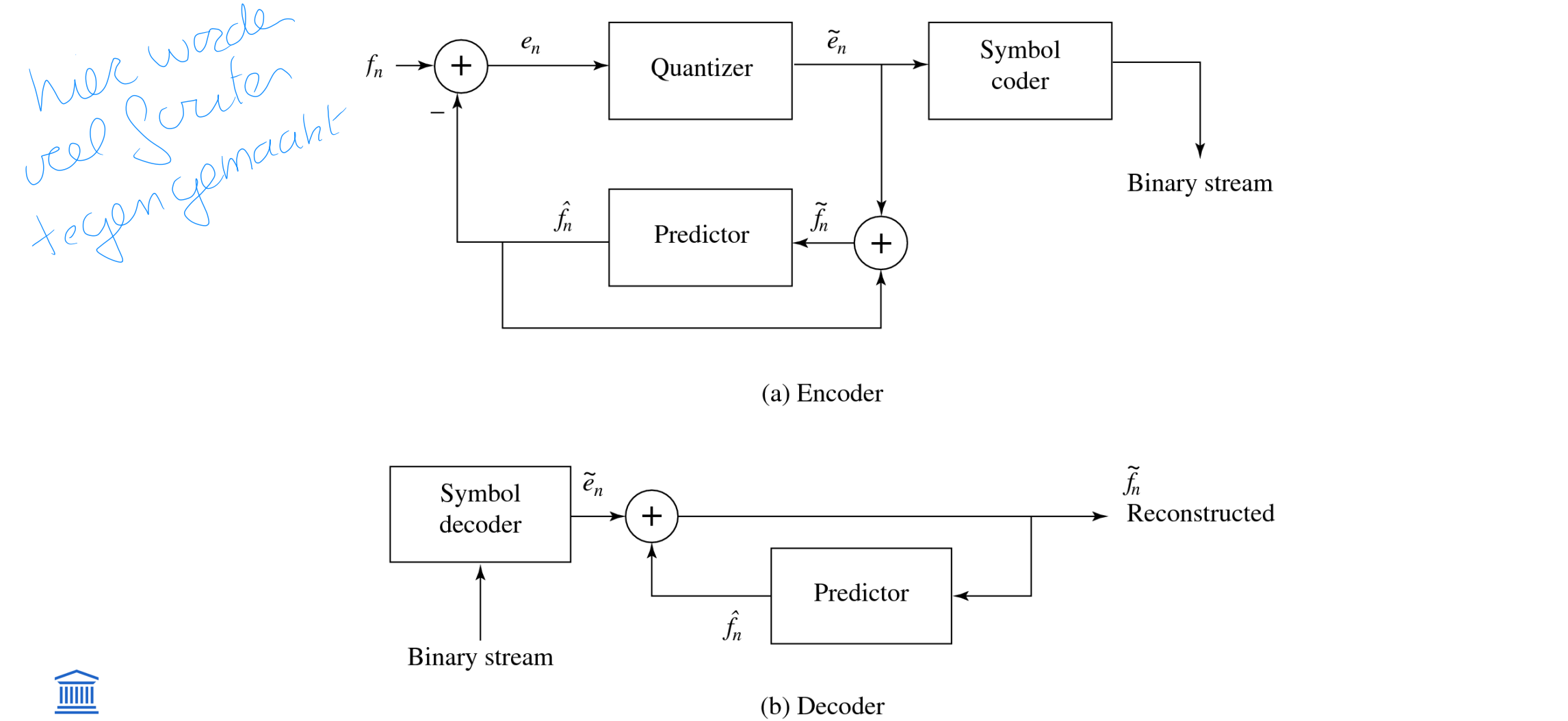
• Nomenclature:

  • signal values fn: the original signal

  • ^fn : the predicted signal

  • ~fn : the quantized, reconstructed signal

Steps in a DPCM encoder:

1. form the prediction

2. form error en by subtracting the prediction from the actual signal

3. quantize the error to a quantized version ~en

   1. 

4. assign codewords for quantized error values ~en using entropy coding, e.g. Huffman coding (Chapter 6)

The distortion is the average squared error ( en - ~en = fn - ~fn)

One often plots distortion versus the number of bit levels used. A Lloyd-Max quantizer will do better (have less distortion) than a uniform quantizer

extra:

• in predictor: gebruik maken van fn → effectieve signalen, ipv de gereconstrueerde ~fn

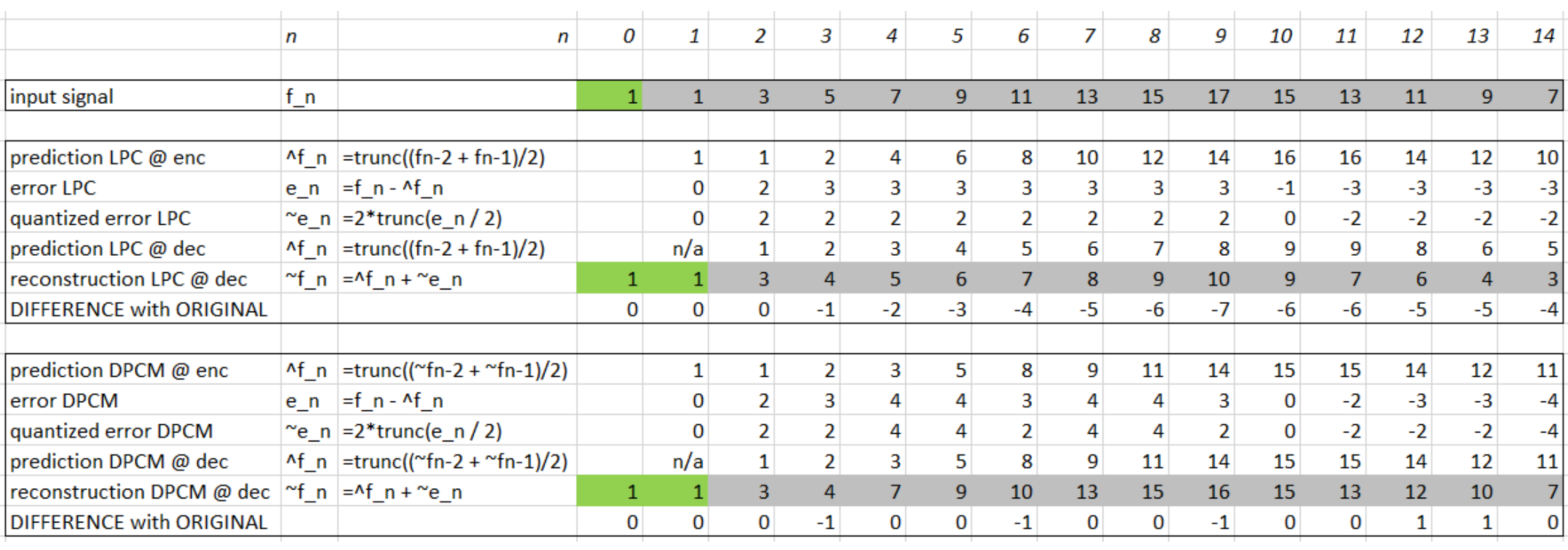
voorbeeld DCPM

Belang van feedback loop bij dpcm

als je quantization toepast op e_n in normal forward LPC veroorzaak je drift

(drift = niet in sync zijn van encoder en decoder)

Delta modulation

• uniform delta DM

• adaptive DM

Simplified version of DPCM, often used as a quick AD converter

Uniform-Delta DM: een enkele gekwantiseerde fout waarde, positief of negatief (1-bit coder)

• produces coded output that follows the original signal in a staircase fashion.

• the prediction simply involves a delay.

• the set of equations is:

  

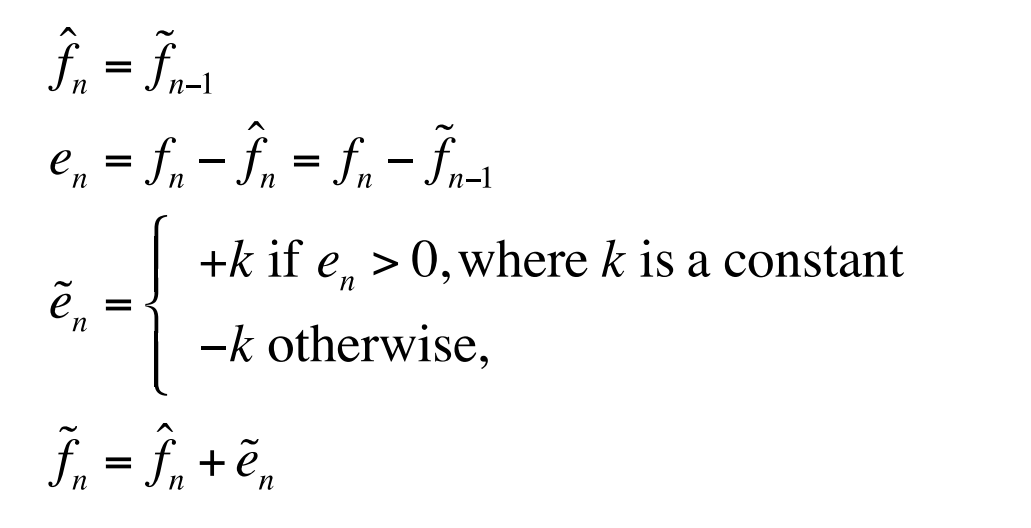
However, DM copes less well with rapidly changing signals. One approach to mitigating this problem is to simply increase the sampling, perhaps to many times the Nyquist rate.

Adaptive DM
If the slope of the actual signal curve is high, the staircase approximation cannot keep up. For a steep curve, one could/should change the step size k adaptively

Adaptive DPCM

ADPCM (Adaptieve DPCM)

ADPCM bouwt verder op DPCM door de coder dynamisch aan te passen aan het invoersignaal.
DPCM bestaat uit twee hoofdcomponenten:

• de quantizer (kwantisator)

• de predictor (voorspeller)

---

Aanpassen van de kwantisator

We kunnen de stapgrootte en de beslissingsgrenzen aanpassen door een niet-uniforme kwantisator te gebruiken.

• Voorwaartse adaptieve kwantisatie:
  → gebruikt eigenschappen van het invoersignaal zelf.

• Achterwaartse adaptieve kwantisatie:
  → gebruikt eigenschappen van het gekwantiseerde outputsignaal
  → Als de kwantisatiefouten te groot worden, moet je de niet-uniforme kwantisator aanpassen.

---

Aanpassen van de voorspeller

We kunnen ook de voorspeller aanpassen door de voorspellingscoëfficiënten aan te passen.

• Dit kan via voorwaartse of achterwaartse aanpassing

• Soms heet dit ook Adaptive Predictive Coding (APC)

Let op:

• De voorspeller is meestal een lineaire functie van eerdere gereconstrueerde gekwantiseerde waarden.

• Het aantal vorige waarden dat je gebruikt heet de orde van de voorspeller.
   → Als je M vorige waarden gebruikt, heb je M coëfficiënten nodig:
    a₁, a₂, ..., a_M

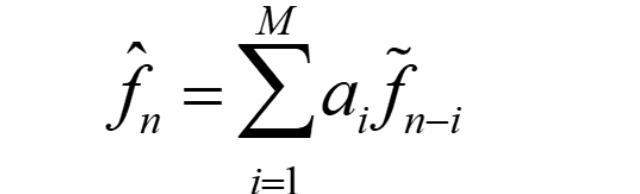
Wanneer we de predictiecoëfficiënten willen aanpassen die vermenigvuldigen met eerdere gekwantiseerde waarden, krijgen we een complex stelsel van vergelijkingen dat moeilijk oplosbaar is.

• Stel dat we een least-squares-benadering gebruiken om de beste waarden te vinden van de coëfficiënten a_i

  

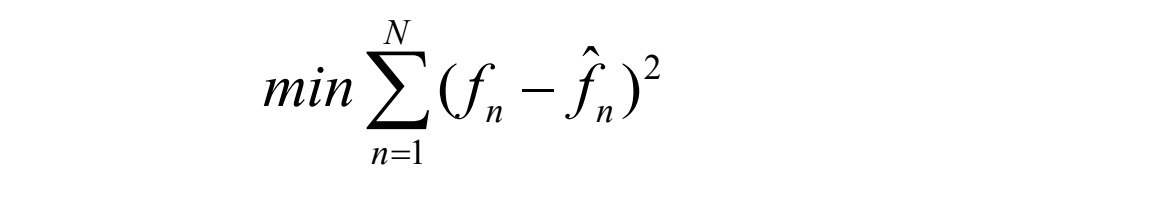
• Uitleg:

  • Hier sommeren we over een groot aantal samples fnf_nfn​, van een huidige spraaksegment.

  • Maar omdat f^n afhankelijk is van de kwantisatie, wordt dit moeilijk oplosbaar.

  • Idealiter zouden we tegelijk ook de fijnheid van de kwantisatie moeten aanpassen aan het signaal. Dit maakt het probleem nog complexer.

• In plaats daarvan gebruikt men typisch een eenvoudiger probleem:

  Gebruik niet f^n​ (de gekwantiseerde voorspelling), maar gewoon f_n​ zelf in de voorspelling.

  

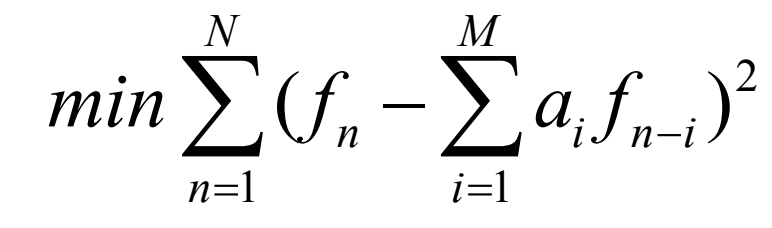
• Differentiation with respect to each of the ai​, and setting to zero, produces a linear system of M equations that is easy to solve.(The set of equations is called the Wiener-Hopf equations.)

figuur adpcm

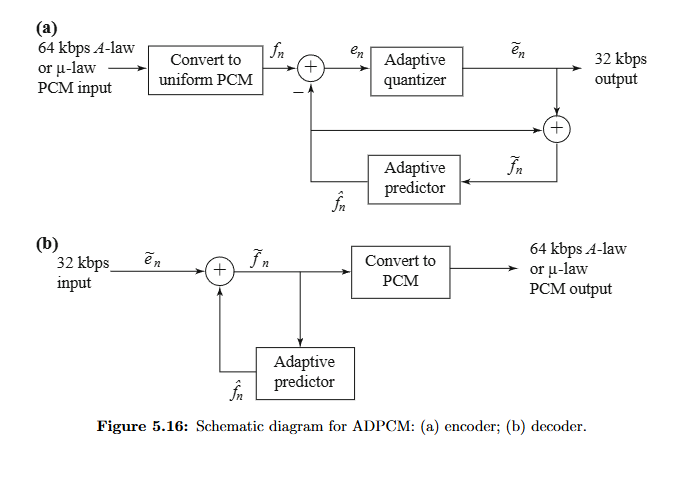
overzicht