exponentials + logs

what is an exponential function

y = a^x

where a>0

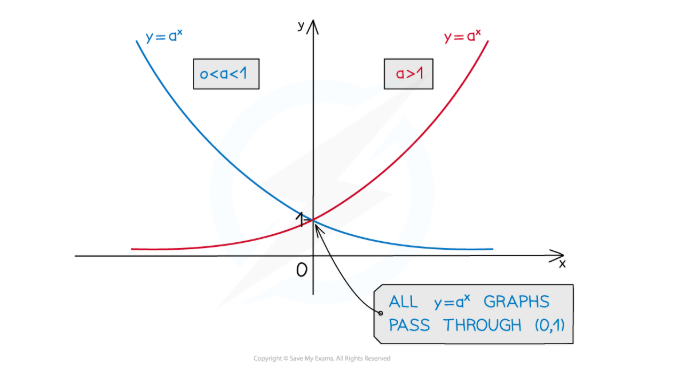
show an exponential graph

all pass through (0,1) - bc anything to the power of 0 is 1

asymptote at x-axis (y will never = 0)

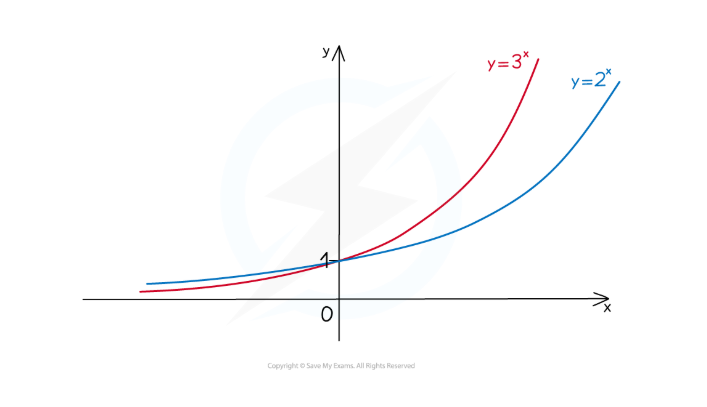
show the difference between the exponential graphs with diff a values, when a is BIGGER THAN ONE

bigger = further in + steeper

show the difference between the exponential graphs with diff a values, when a is SMALLER THAN ONE

smaller = further in + steeper

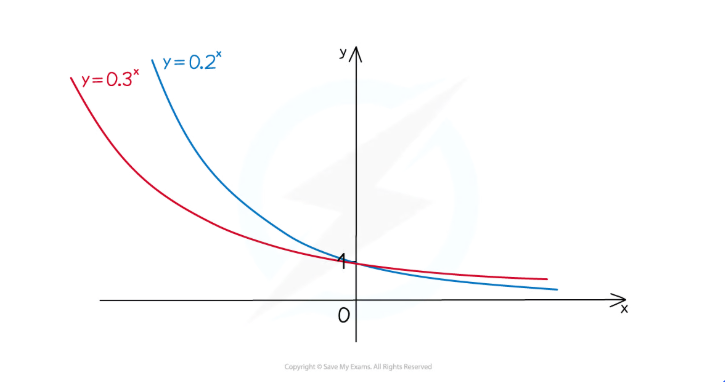
a>1 vs 0<a<1

a bigger than 1 = exponential GROWTH

a smaller than 1 = exponential DECAY

why is a=1 not considered

would be a straight line —> 1 to the power of anything is 1

another way of writing a = b^x

log _b a = x

you’d say “log base b of a = x”

aka: what power of b do you need to create a?

what about negative numbers

you can’t log negative numbers (in the a-level course)

what are some useful log shortcuts

log x = log base 10 of x

ln x = long base e of x (aka natural log of x)

what is e

an irrational number

= 2.718

has a special property:

the function y = e^x gives a differntial of e^x as well!! (gradient the same as function)

usual function for exponential growth

y = Ae^kx

y = y coordinate

A = initial value

e = e

k = constant

x = x coordinate (t often used tho to depict time)

usual function for exponential decay

y = Ae^-kx

y = y coordinate

A = initial value

e = e

k = constant

x = x coordinate (t often used tho to depict time)

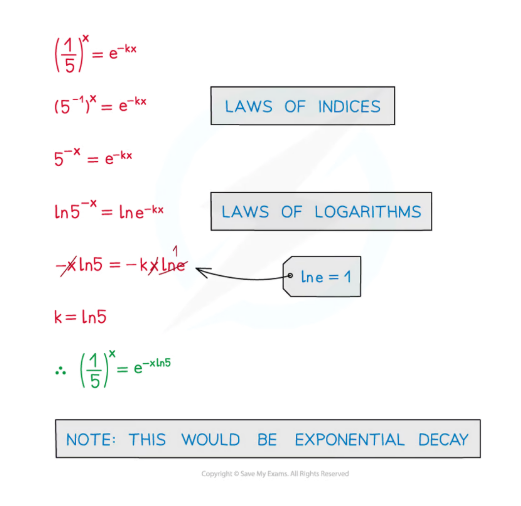
how to rewrite a normal exponential function into one involving e

basically take ln of both sides then solve for k

how to differentiate y = e^kx

.

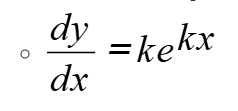
how to differentiate y = e^-kx

.

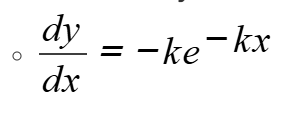
log law involving adding (and where it comes from if u can)

log_ax + log_ay = log_a(xy)

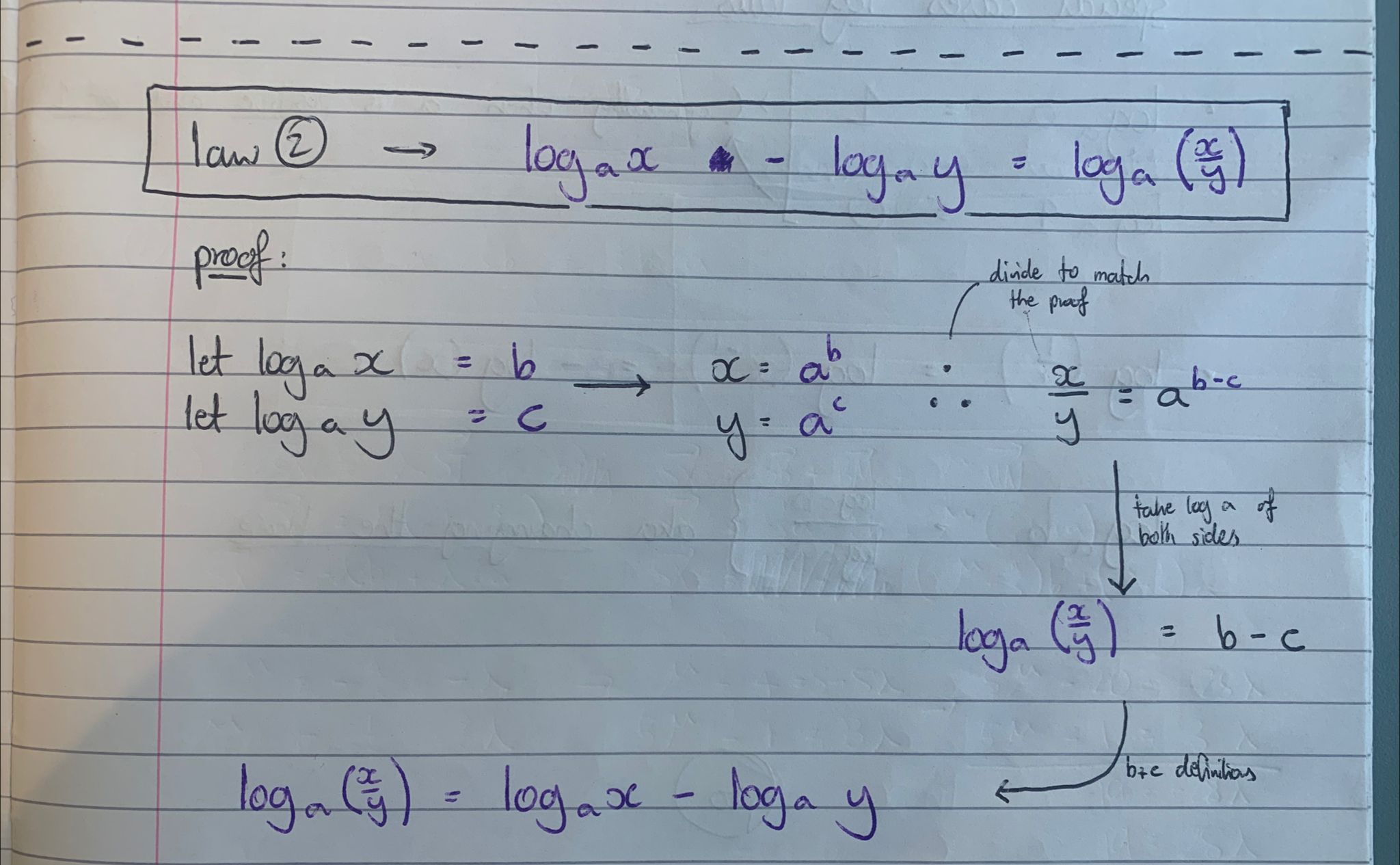
log law involving subtracting (and where it comes from if u can)

log_ax - log_ay = log_a(x/y)

log law involving powers (and where it comes from if u can)

log_a(x^k) = k(log_ax)

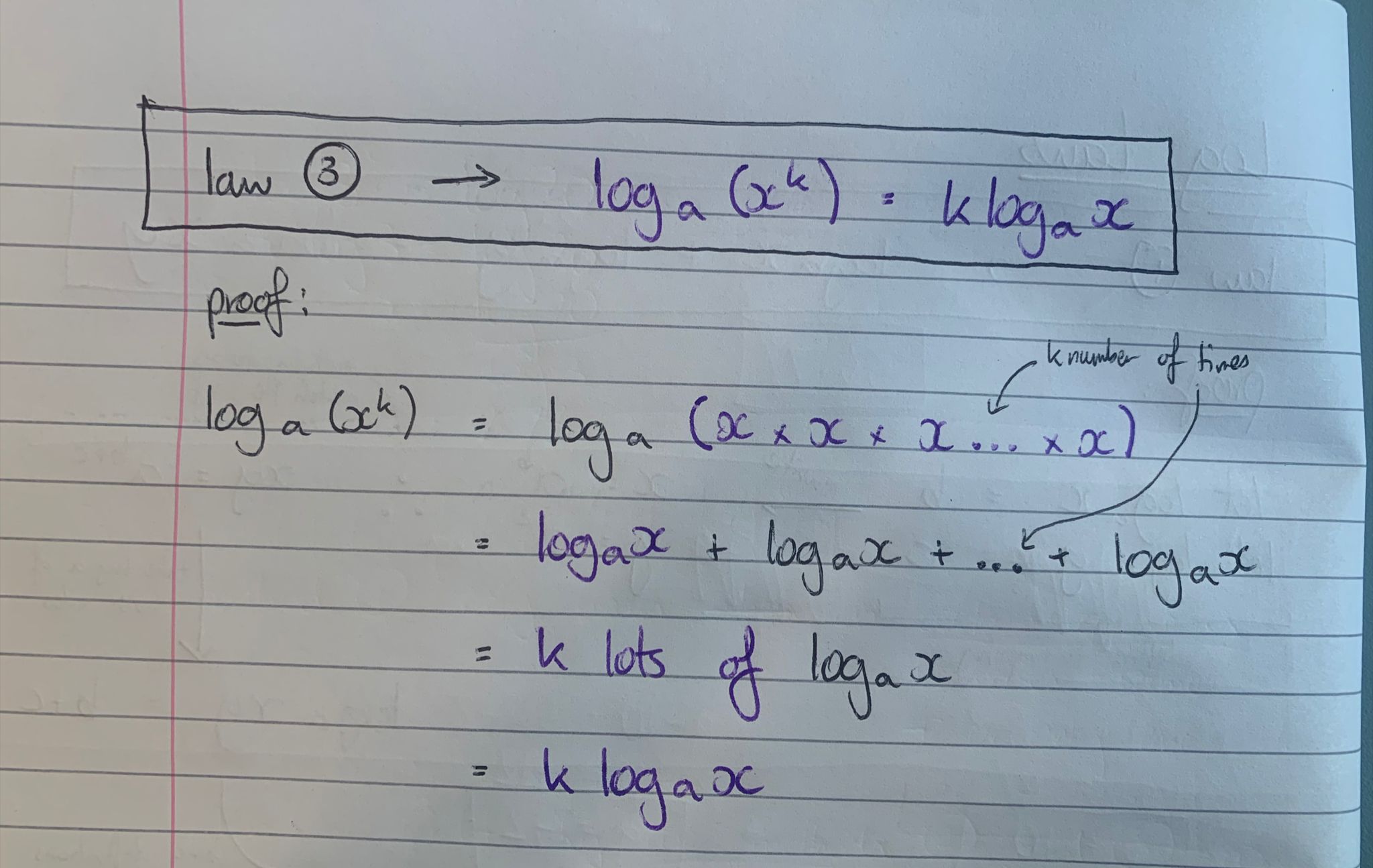
other smaller rules that are good to know

see the picture

two extras are also:

• log_a(a^x) = x

• a^(log_ax) = x

best way of solving exponential equations

take ln of both sides

what might they put in logs questions

hidden quadratics - watch out for them!

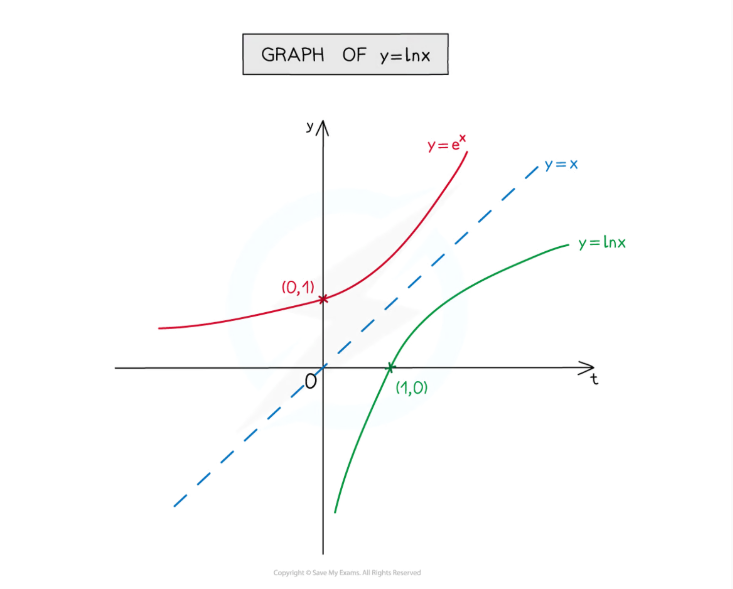
how do graphs of the log of something look compared to their respective exponential graphs

hit the x axis at (1,0)

its basically a reflection in the line y=x

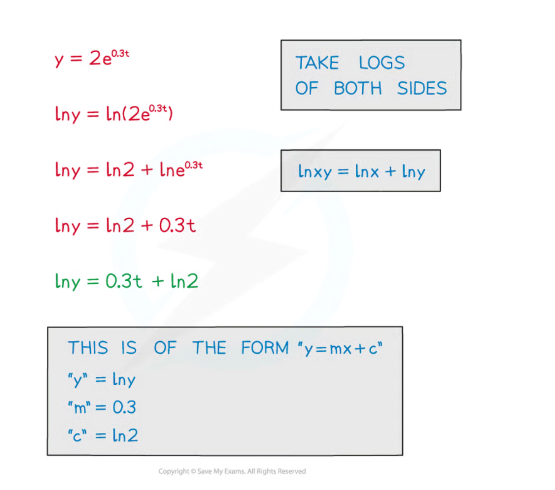
how to turn an exponential graph into a linear log graph

take ln of both sides (if e is involved - otherwise just take logs)

the graph will have at least one logarithmic axis

the equation will become y = mx + c (just with diff things for m and c)

best way to practice graphs in this topic

use desmos so u see how they work!