Calculus - Limits and Some Derivatives

indeterminant form

when you take the limit and the result is 0/0

factoring techniques

• change of variable

• diff of squares

• diff/sum of cubes

• grouping

• common factoring

• trinomial factoring

• factor theorem

• breaking shit down

floor function

f(x) that outputs the greatest integer less than or equal to x

requirements for continuity

• no breaks in individual domains

• left one-sided limit = right one-sided limit

• limit = output of function

a function is continuous at a point if:

the limit taken of the input = the output given by the function

slope from tangent line definition (formula)

derivative f’(x)

a fn is differentiable at a point provided that

f’(t) exists (the limit as h approaches 0 exists)

a fn is differentiable on an interval provided that:

• for all points (t) inside the interval domain, f’(t) exists

if a fn is differentiable, it is

continuous

if a fn is continuous, it is

not necessarily differentiable

for parts on the graph f(x) where the slope appears steep, it would

form a VA at the x-coord on the differentiablity graph f’(x)

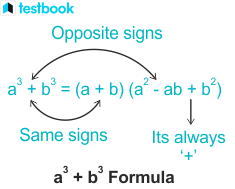
sum and diff of cubes

diff of cubes is like the same logic but obvi looks opposite

limit properties

function is discontinuous if

• limit when approaching from the right does not equal the limit when approaching from the left

• limit of the val does not equal the output of the function when you input the val

checking continuity →

• check endpoints

completing the square

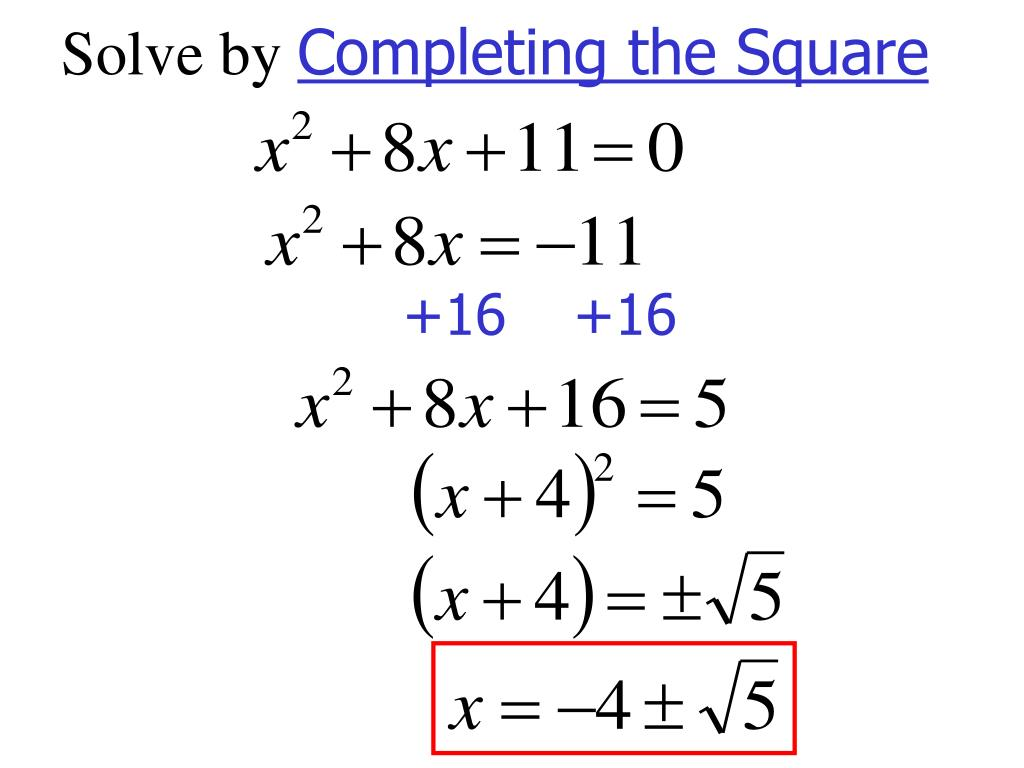
when do limits not exist

• at a vertical asymptote

• when one-sided limits are not equal

(x²-1)^ 3 =

(x-1)³(x+3)³

where is a function not differentiable?

where the derivative of the function is undefined (check the domain)