15 Increasing/Decreasing, Concavity of Functions, Relative and Absolute Extrema

What happens to the slope when function is increasing?

(1) slope/derivative is positive

What happens to the slope when functions is decreasing?

(1) slope/derivative is negative

If f’(x) > 0 on (a, b), then…

(If your derivative or slope is positive then your) Function is increasing

If f’(x) < 0 on (a, b), then…

(If you derivative or slope is negative then your) Function is decreasing

If f’(x) = 0 then…

(If your derivative or slope is zero then your) Function is a horizontal line

What is concavity?

(1) the second derivative 

(2) how a curve is increasing or decreasing, at a slower rate or at a faster rate

What happens to the slope when it’s decreasing and increasing as it concaves up?

(1) flatter, decreasing at an increasing rate (at a higher point the slope goes from more negative to less negative as it goes down)

(2) steeper, increasing at an increasing rate

What happens to the slope when it’s increasing and decreasing as it concaves down?

(1) flatter, increasing at a decreasing rate

(2) steeper, decreasing at a decreasing rate (at a higher point the slope goes from negative to more negative as it goes down)

Point of Inflection

(1) the point where you change concavity

(2) when the slope becomes zero

If f’’(x) > 0, then

(If the second derivative is positive, then you get a) Concave up

If f’’(x) < 0, then

(If the second derivative is negative, then you get a) Concave down

If f’’(x) = 0, then

Possible inflection point

Relative Max

(1) peak of an interval

(2) highest point of an interval

(3) relative max: function changes from increasing to decreasing

Relative Min

(1) lowest point of an interval

(2) relative min: function changes from decreasing to increasing

What happens to the slope when you approach relative max or min?

(1) the slope becomes zero

Critical Number

(1) the number or point at which a curve has a horizontal tangent, where the slope equals zero

(2) the place or period where your slope equals zero

Steps to Solving for the Critical Point

Step 1: Take the first derivative of your function

Step 2: Set first derivative equal to zero
**If you have a denominator, set the denominator to zero and that could give you any undefined points aswell

What is the absolute max?

(1) the highest point on an interval

What is the absolute min?

(1) the lowest point on an interval

Do all graphs have absolute max/min on (−∞,∞)?

Some graphs don’t such as:

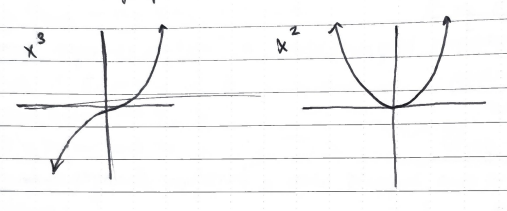
Absolute Max and Min on Closed Intervals

(1) on any continuous closed interval, absolute max/min will occur at either the critical numbers or the endpoints

Absolute Max and Min on Open Intervals

(1) if they occur, they must do so at the critical numbers

Steps to Find the Absolute Max/Min

Step 1: Find the derivative/slope

Step 2: Set derivative/slope equal to zero to find the critical numbers (isolate, factor, rationalize)

Step 3: Take critical points and the given interval and set up a T-table to plug in x values into the original function

Step 4: Discern, once you plug in the numbers, your outputs f(x) will give you the heights

How to Factor GCF w/Rational Exponents

Step 1: Pick the x-variable with the lowest value exponent

Step 2: Divide the inside by the one you’ve factored out