Precalc Flashcards

To find the y-intercept of a function

Let x = 0 and solve for y.

To find the x-intercept of a function

Let y = 0 and solve for x.

The only way for a fraction to equal zero is if…

the numerator equals zero

How do you know when a rational function has a hole?

It contains the same factor in the numerator and denominator

How do you know when a rational function has a vertical asymptote?

There is a real factor in the denominator that does not appear in the numerator.

What do you look at to determine a horizontal asymptote?

The degree of the numerator and the denominator.

If the degree of the numerator is less than the degree of the denominator

y = 0 is a horizontal asymptote

If the degree of the numerator is equal to the degree of the denominator

Look at the leading coefficients of the numerator and denominator

If the degree of the numerator is greater than the degree of the denominator

There is no horizontal asymptote (look for a slant asymptote)

Increasing Function

If a < b,

then f(a) < f(b)

If the rate of change of a function is positive on an interval

the function is increasing on that interval

Decreasing Function

If a < b,

then f(a) > f(b)

If the rate of change of a function is negative on an interval

the function is decreasing on that interval

Concave UP

The rate of change is INcreasing

Concave DOWN

The rate of change is DEcreasing

Rate of Change formula

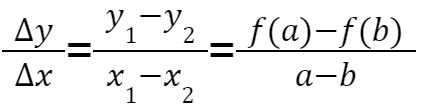
Rate of Change What it means

Slope of a secant line

If the rate of change of g(x) is increasing on an interval

g(x) is Concave UP on the interval

If the rate of change of g(x) is decreasing on an interval

g(x) is Concave DOWN on the interval

Parent function - linear

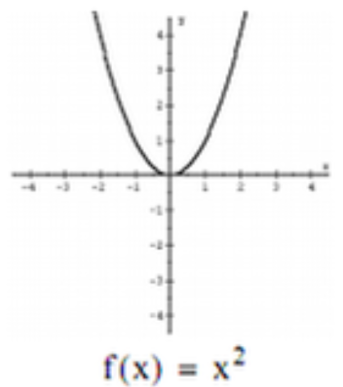
Parent Function - Quadratic

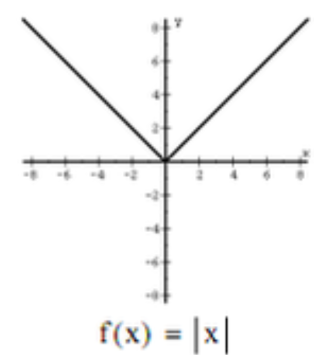
Parent function - absolute value

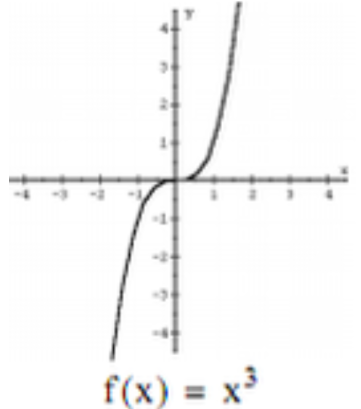
Parent Function - Cubic

Parent function - Square root

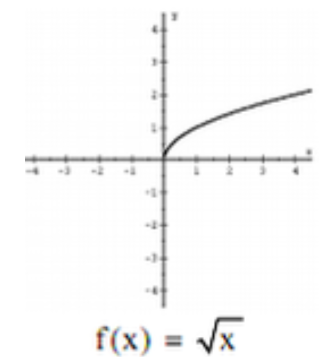
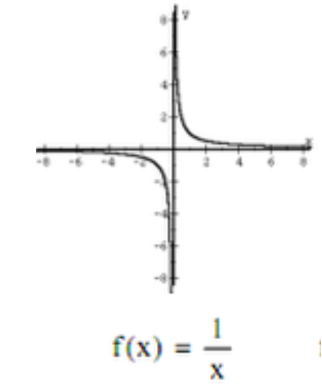
Parent function - reciprocal

inflection point

A point where a function’s graph changes concavity

Even Function

f(-x) = f(x)

Symmetric across y-axis

Odd function

f(-x) = -f(x)

Symmetric across the origin

Sum of Cubes

a³ + b³ = (a + b) (a² - ab + b²)

Difference of Cubes

a³ - b³ = (a - b)(a² + ab + b²)