D420 Discrete Math: Logic

proposition

a statement that is either true or false

^

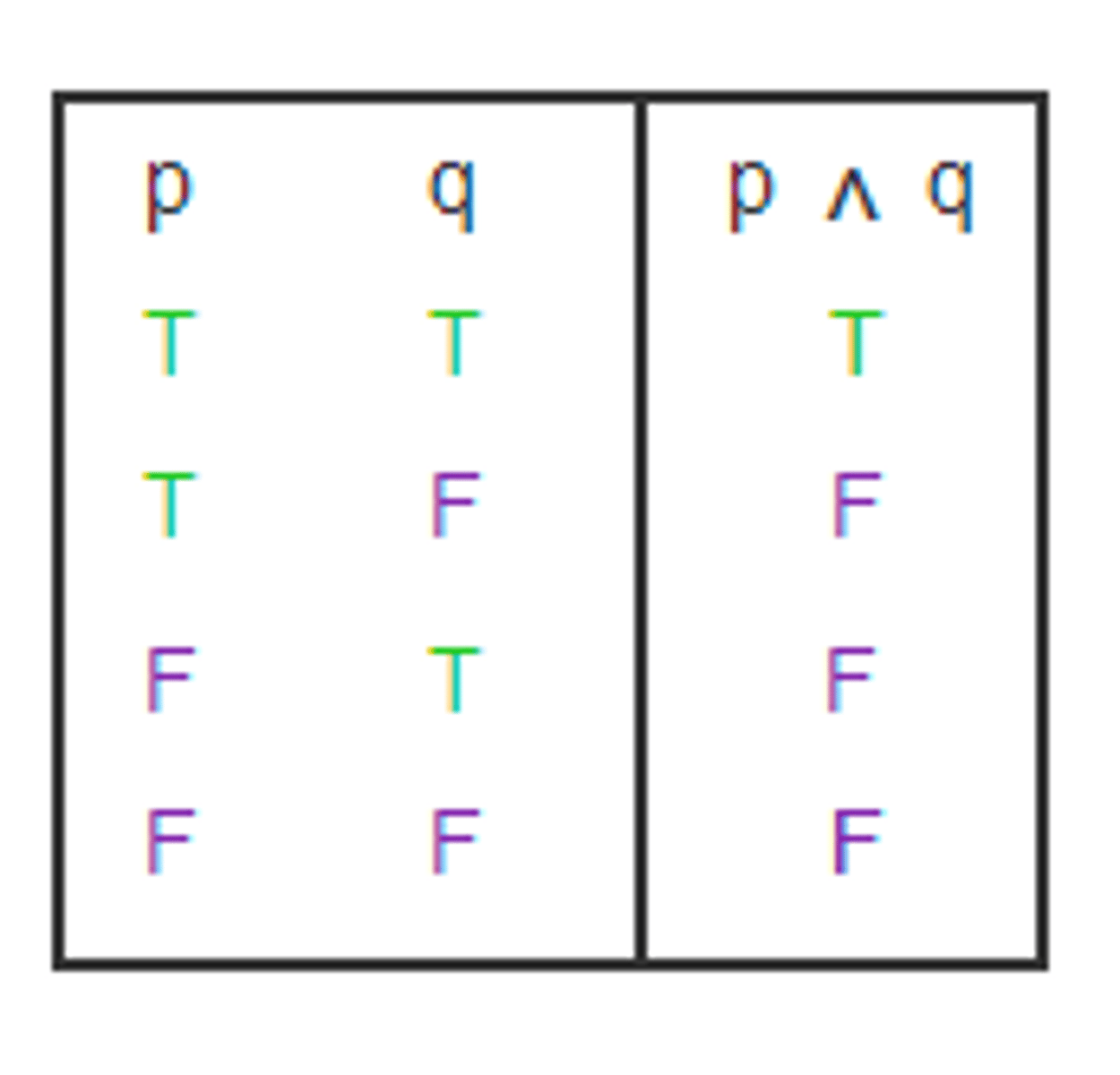
and

v

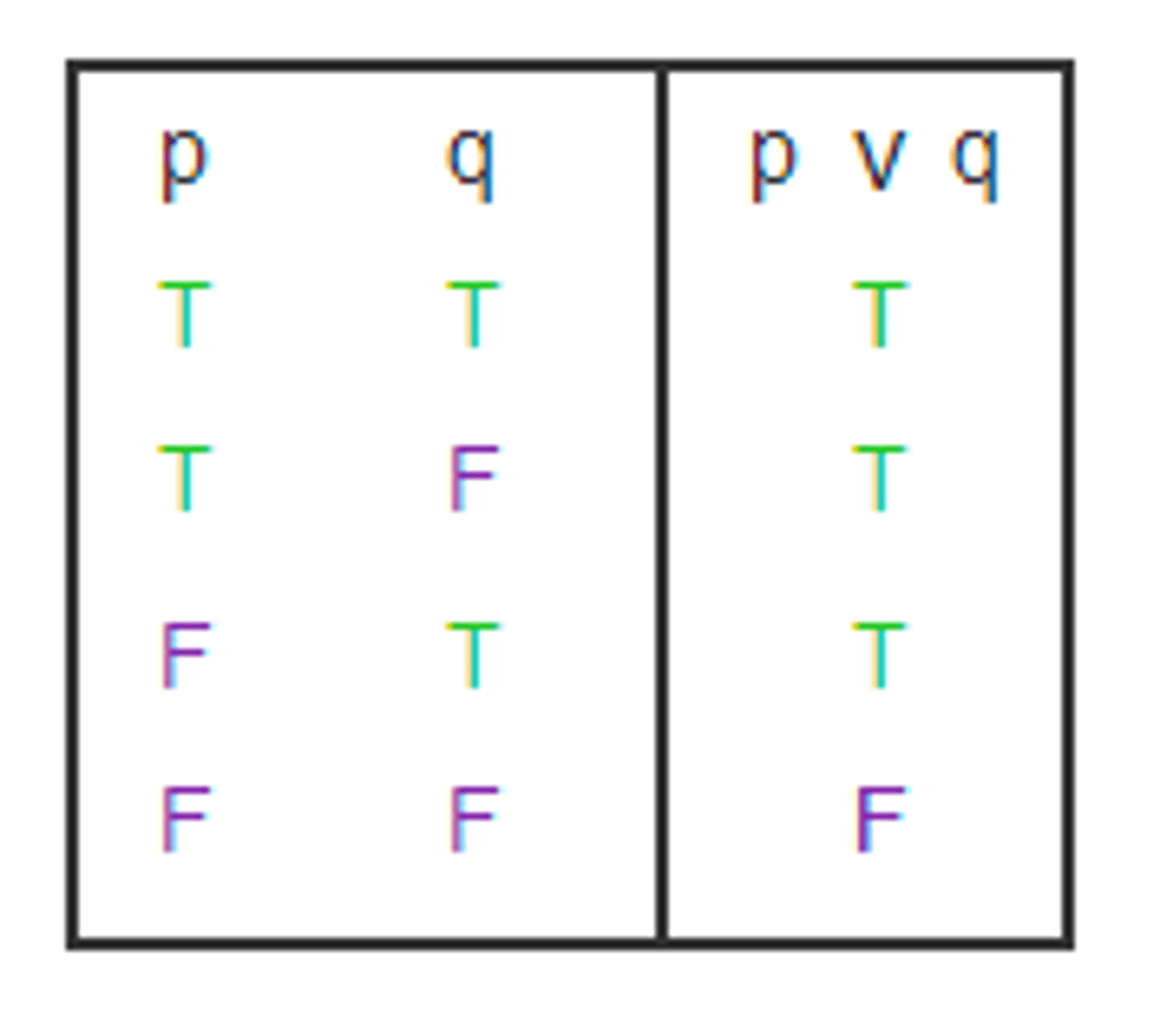
or

¬

negation

→

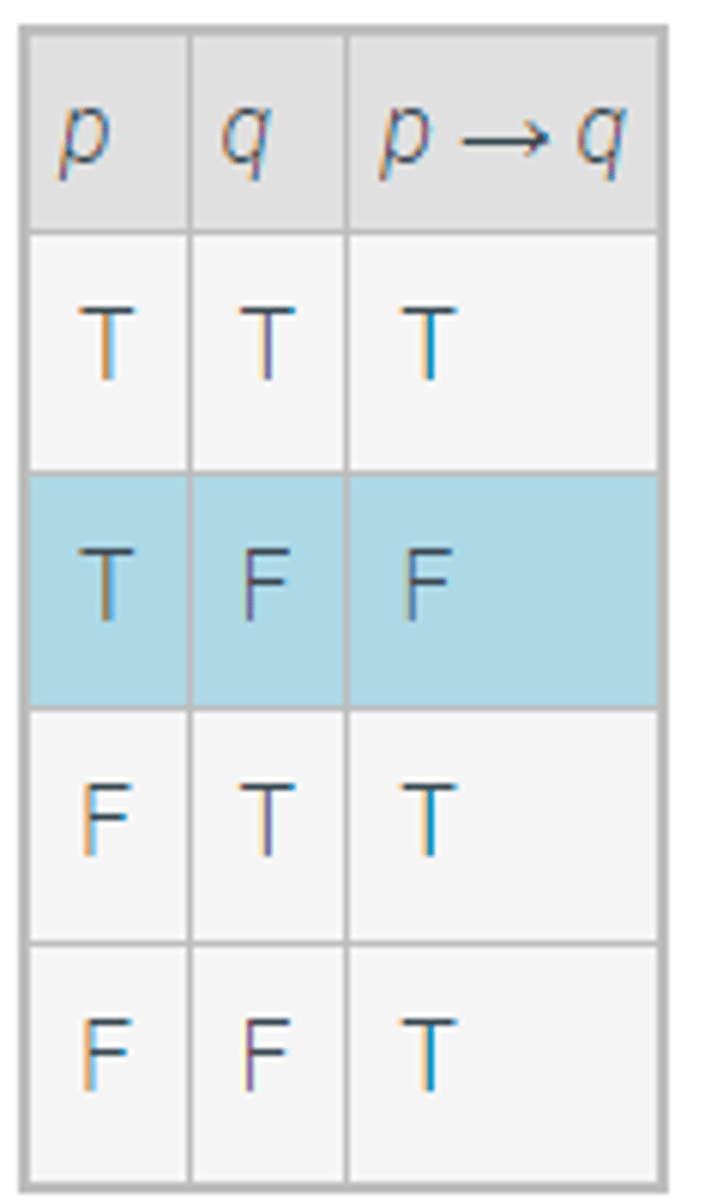
conditional operation, "if p, then q"

Equivalent English expressions that mean "if p, then q"

If p, q

q, if p

p implies q

p only if q

p is sufficient for q

q is necessary for p

in a conditional proposition "→" p is the _______ and q is the __________

p is the hypothesis and q is the conclusion

The converse is the opposite of the conditional statement

For example, the converse of p → q (if p then q) is q → p (if q then p). If p → q is true, it does NOT guarantee that q → p is true

The inverse is the negation of the conditional statement

For example, the inverse of p → q (if p then q) is ¬p → ¬q (if not p then not q). If p → q is true, it does NOT guarantee that ¬p → ¬q is true

The contrapositive is the opposite and negative of the conditional statement

For example, the contrapositive of p → q (if p then q) is ¬q → ¬p (if not q then not p). If p → q is true, it DOES guarantee that ¬q → ¬p is true

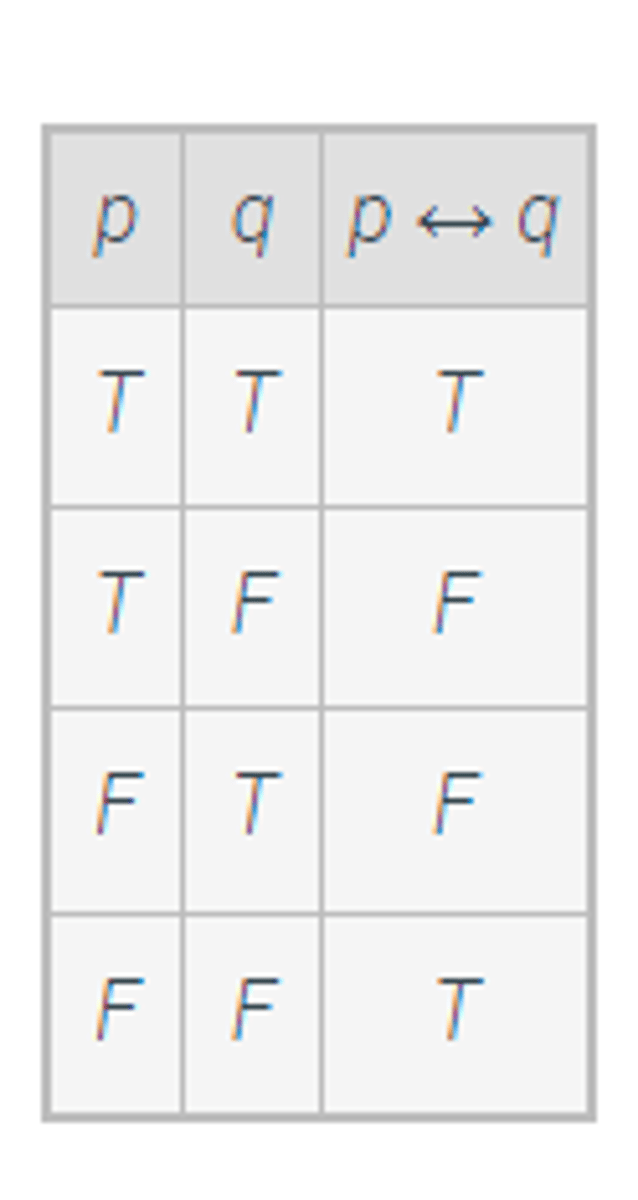
biconditional operation

is read "p is necessary and sufficient for q" or "if p then q, and conversely" or "p if and only if q"

Logical equivalence p ≡ q

Two compound propositions are logically equivalent if they have the same truth value. That is, the truth value in the final column in a truth table is the same for both compound propositions

tautology

If the compound propositions is always true. For example, p∨¬p.

contradiction

if the compound proposition is always false. For example, p∧¬p.

De Morgan's Law

logical equivalences that show how to correctly distribute a negation operation inside a parenthesized expression containing the disjunction or conjunction operator.

¬(p ∨ q) = (¬p ∧ ¬q)

¬(p ∧ q) = (¬p ∨ ¬q)

Absorption laws

p ∨ (p ∧ q) ≡ p

p ∧ (p ∨ q) ≡ p

Associative laws

(p ∨ q) ∨ r ≡ p ∨ (q ∨ r)

(p ∧ q) ∧ r ≡ p ∧ (q ∧ r)

Commutative laws

p ∨ q ≡ q ∨ p

p ∧ q ≡ q ∧ p

Complement laws

p ∧ ¬p ≡ F

¬T ≡ F

p ∨ ¬p ≡ T

¬F ≡ T

Conditional identities

p → q ≡ ¬p ∨ q

p ↔ q ≡ ( p → q ) ∧ ( q → p )

Distributive laws

p ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r)

p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r)

Domination laws

p ∨ T ≡ T

p ∧ F ≡ F

Double negation law

¬(¬p) ≡ p

idempotent laws

p ∨ p ≡ p

p ∧ p ≡ p

identity laws

p ∧ T ≡ p

p ∨ F ≡ p

predicate

a logical statement whose truth value is a function of one or more variables

domain of the predicate

the set of all possible x values for P(x) is called the domain of the predicate

universal quantifier

"for all x", is denoted ∀x, P(x). This means that for all values of x in the domain of P(x), the predicate is true.

existential quantifier

"there exists an x" such that P(x) is denoted ∃x, P(x). This means there is at least one x in the domain of the predicate that yields a truth value for P(x).

To show that ∀x, P(x) is not a true statement

we need only show for one x, P(x) is false.

To show that ∃x, P(x) is not a true statement

we need to show for all values of x, P(x) is false

free variable

A variable x in the predicate P(x) is called a free variable because it is not quantified. That is, the variable is free to take on any value in the domain.

bound variable

The variable x in the statement ∀xP(x) is a bound variable because it is quantified. That is, the variable is bound to a quantifier.

If statement has no free variables...

then the statement is a proposition because its truth value can be determined

DeMorgan's laws for quantified statements

¬∀xP(x) ≡ ∃x¬P(x)

¬∃xP(x) ≡ ∀x¬P(x)

DeMorgan's law for quantified statements are the same laws for propositions

nested quantifiers

A logical expression with more than one quantifier that binds different variables in the same predicate

∀x∀y M(x,y)

For every pair of x and y, M(x,y) is true

∃x∃y M(x,y)

There exists at least one pair of x and y such that M(x,y) is true

∃x∀y M(x,y)

There exists at least one x that pairs with ALL y, such that M(x,y) is true

∀x∃y M(x,y)

For each x, there is at least one y, such that M(x,y) is true

DeMorgan's law with nested quantifiers

¬∀x ∀y P(x, y) ≡ ∃x ∃y ¬P(x, y)

It is not true for all x and for all y, P(x, y).

There exists at least one pair (x, y) such that P(x, y) is false.

DeMorgan's law with nested quantifiers

¬∀x ∃y P(x, y) ≡ ∃x ∀y ¬P(x, y)

It is not true for all x there exists a y, such that P(x, y) is true

There exists at least one x and for all y, P(x, y) is false.

DeMorgan's law with nested quantifiers

¬∃x ∀y P(x, y) ≡ ∀x ∃y ¬P(x, y)

It is not true that there exists an x for all y, such P(x, y) is true

For all x, there is at least one y, such that P(x, y) is false.

DeMorgan's law with nested quantifiers

¬∃x ∃y P(x, y) ≡ ∀x ∀y ¬P(x, y)

It is not true that there exists a pair of x and y, such that P(x, y) is true.

For every pair of (x, y), P(x, y) is false.

argument

consists of a collection of propositions that include a set of premises called the hypotheses and a concluding one called the conclusion. Symbolically, we use p1, p2, ... pn to represent the hypotheses and c for the conclusion.

argument is expressed as

(p1 ∧ p2∧ ... ∧ pn) → c

A proposition can be true or false whereas an argument is

valid or invalid

The argument is valid if...

all the premises are true AND the conclusion is true. It is invalid otherwise.

Modus ponens

Given p;

if p then q;

then q can be inferred

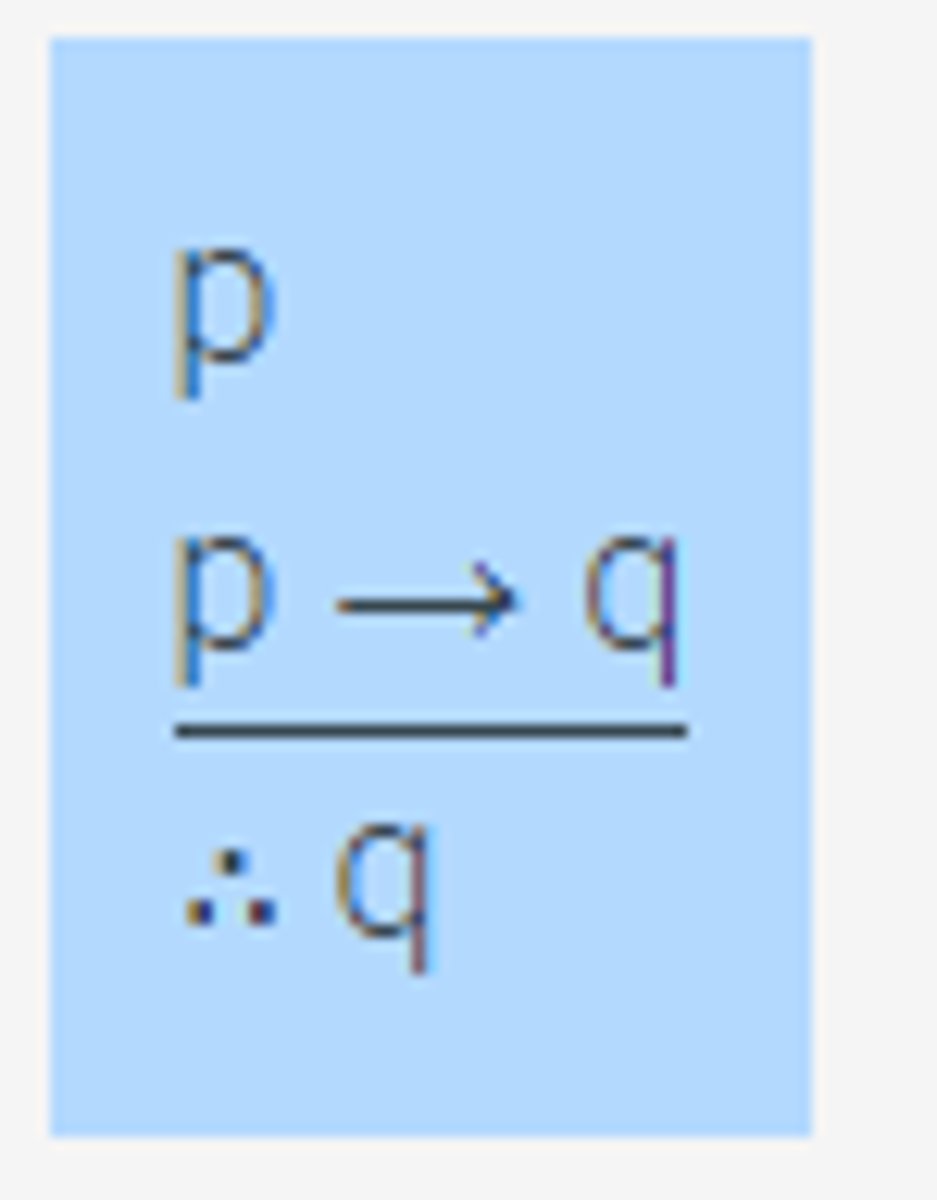
Modus tollens

Given NOT q;

if p then q;

then NOT p can be inferred

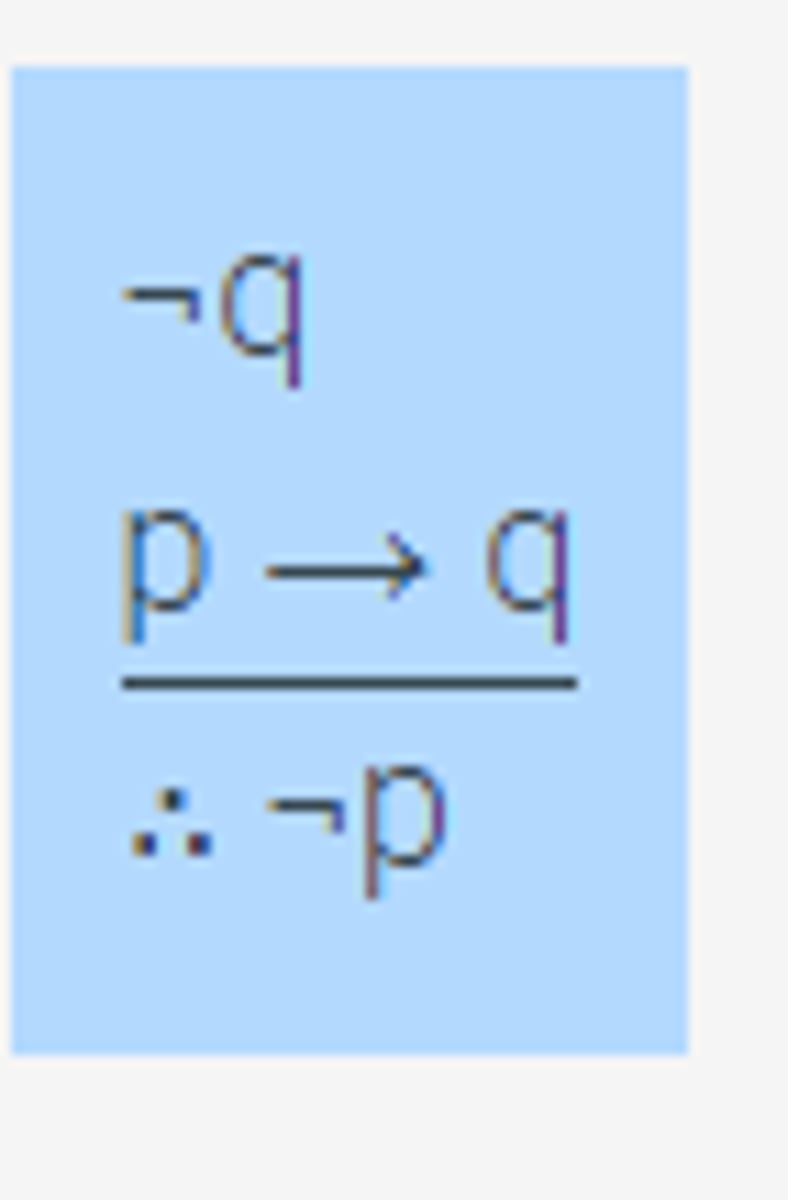
Addition

Given p;

p OR q can be inferred

Simplification

Given p AND q;

p can be inferred

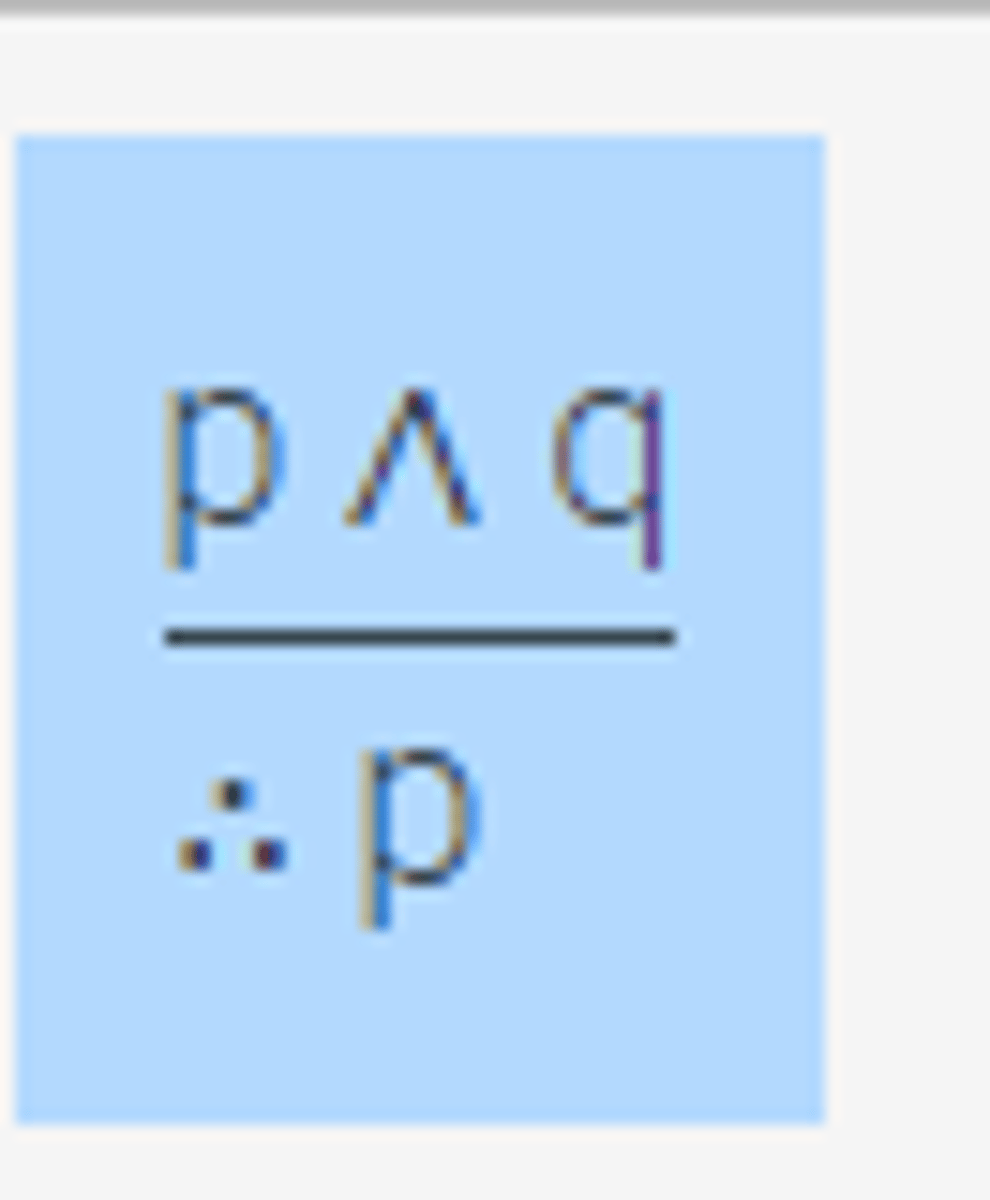
Conjunction

Given p;

Given q;

p AND q can be inferred

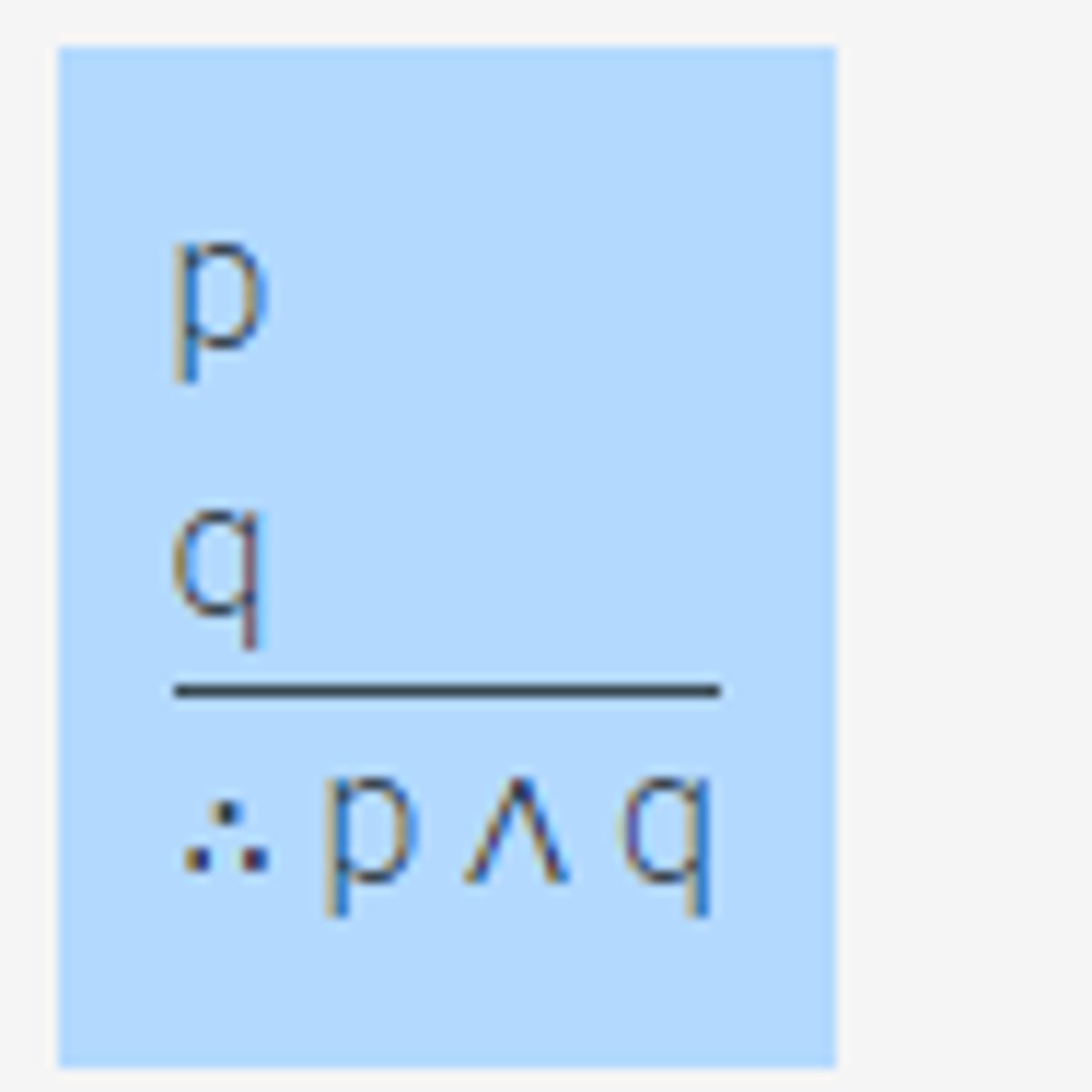
Hypothetical syllogism

If p implies q;

and q implies r;

Then p implies r can be inferred

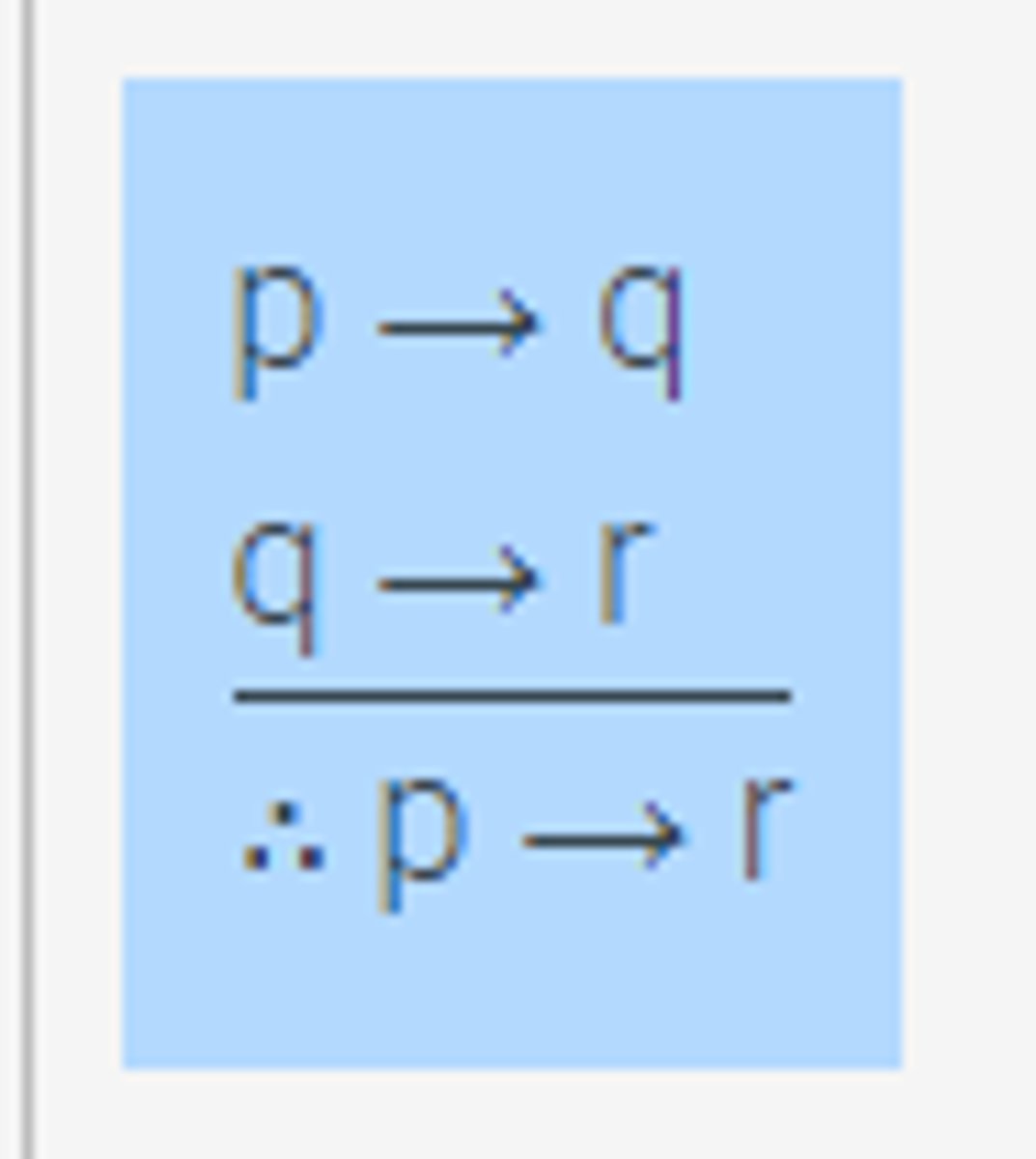
Disjunctive syllogism

Given p OR q;

Given NOT p;

Then q can be inferred

Resolution

Given p OR q ;

Given NOT p OR r;

Then q OR r can be inferred

elements

arbitrary element

An element that refers to any unspecified x in the domain.

For example, "Let x be any element in the domain of P(x)."

particular element

An element that refers to an x in the domain with certain properties

For example, "Let x be in the domain of P(x) such that x is also even."

Universal instantiation

Rule of Inference:

c is an element (arbitrary or particular)

∀x P(x)

∴ P(c)

Explanation:

c is an element

For all of x, P(x)

Therefore, P(c)

Universal generalization

Rule of Inference:

c is an arbitrary element

P(c) ______

∴ ∀x P(x)

Explanation:

Let c be an arbitrary element.

P(c)

Therefore for every x, P(x).

Existential instantiation

Rule of Inference:

∃x P(x)

∴ (c is a particular element) ∧ P(c)

Explanation:

There exists an x, P(x).

Therefore, there is a particular c such that P(c).

Existential generalization

Rule of Inference:

c is an element (arbitrary or particular)

P(c)

∴ ∃x P(x)

Explanation:

There is an element c such that P(c).

Therefore, there exists an x such that P(x).

theorem

a claim that can be proved true using logical arguments

proof

process we use to show the theorem is true

axioms

Claims that we accept to be true without proof

For proofs of universal statements...

a proof by exhaustion is one technique that shows the claim is true for all x in the domain.

To prove a claim is true by exhaustion...

plug each element in the domain with a value and determine its truth value.

For infinite domains and large finite domains...

this process is not possible and one must show the statement is true for an arbitrary element in the domain.

To disprove a universal statement...

find one counterexample to the claim

For example, to disprove the statement, "All prime numbers are odd" find one example where this statement is false—the number 2—which is both even and prime.

Use a direct proof to..

prove a claim implies a conclusion for a conditional statement ().

In a direct proof

start with the hypothesis of a statement and make one deduction after another until you reach the conclusion.

Symbolically, to prove with a direct proof

start with the original claim p then justify a sequential order of steps. The following is the structure of a direct proof.

p and show

p → p1 then

p1 → p2 then

pn → c for a sequence of steps, p1, p2, ... ,pn.

To prove a statement by contraposition, start with the contrapositive of the statement

In this example ¬c→¬p is the contrapositive of p→c. Then prove the contrapositive by a direct proof and conclude that the original statement is true. (For a refresher on direct proofs, review the previous lesson.)

The proof by contrapositive is often used for number theory proofs

It is good to know that the definition of an even number can be expressed as 2n where n is an integer. An odd number can be expressed as 2n + 1 for some integer n.

The proof by contrapositive is often used with statements with rational numbers.

A rational number can be expressed as the quotient of integers. An irrational number is one that cannot.

proof by contradiction

An indirect way to prove a theorem is to assume it is false and then show how, under this assumption, a mathematical contradiction will arise.

To prove by contradiction

start with the conditional statement p→c and assume the premise (p) is true but that conclusion (c) is false. Then proceed to show there is a contradiction using the same steps as the direct proof.

Use proofs by contradiction when it is more difficult to prove the theorem directly

For example, to show that the sum of an irrational number and a rational number is irrational, it is easier to prove it indirectly by assuming the sum is rational and showing that a contradiction arises, than to prove it directly.

proof by cases

To prove a predicate P(x) is true on its domain, sometimes it is easier to show the predicate is true by breaking up the domain into different classes and offering proofs for each class separately.

Boolean algebra

an expansion of the logic chapter covered in a previous unit where true (T) is now represented by 1 and false (F) is now 0.

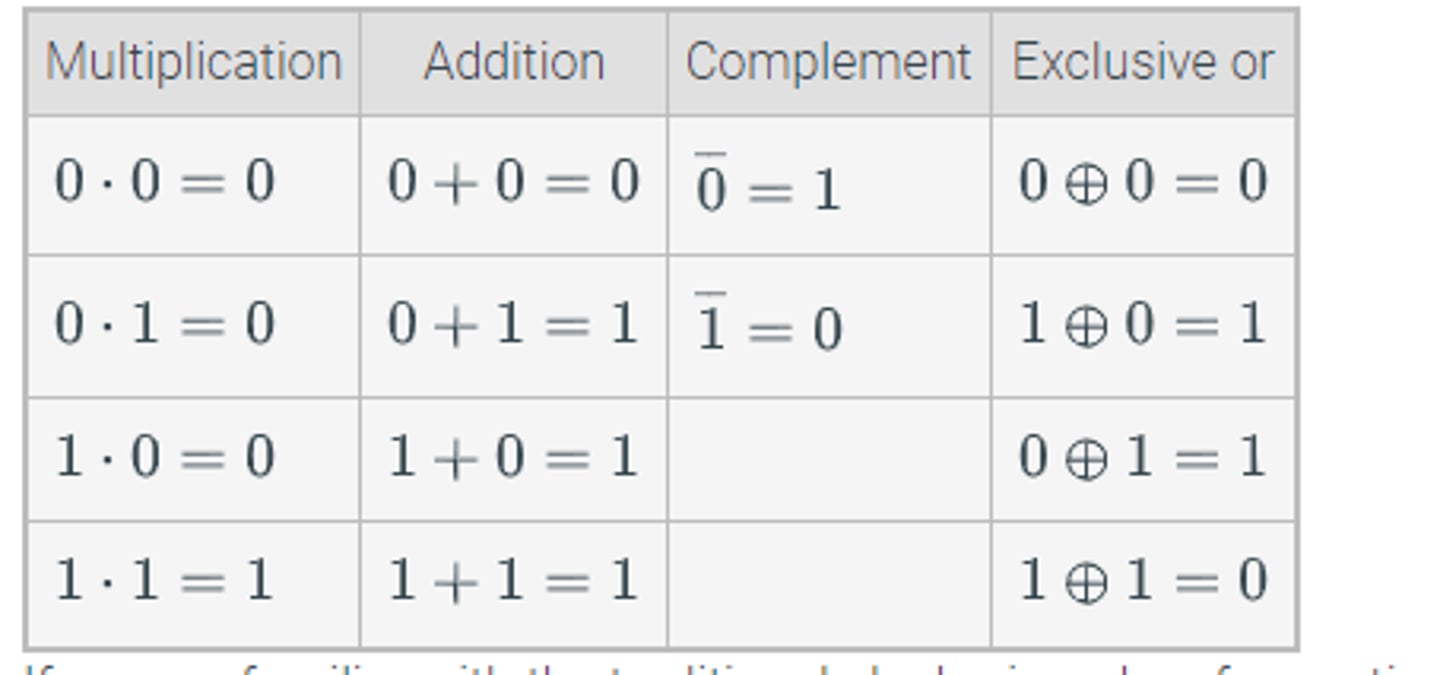
Boolean addition (+)

Logical ∨ (OR)

Boolean multiplication (⋅)

Logical ∧ (AND)

Boolean complement (bar symbol xˉ)

Logical ¬ (NOT)

Boolean exclusive or (⊕)

Logical ⊕ (XOR)

Boolean order of operations

Parentheses can override any other precedence

Complements are calculated before addition or multiplication

Multiplication takes precedence over addition

Absorption laws (Boolean algebra)

Since x ⋅ x requires x, x+(x × y) is just x.

Associative laws (Boolean algebra)

Only applies when the operators are all addition, or are all multiplication. Rearranging the parentheses in an expression will not change the expression's value.

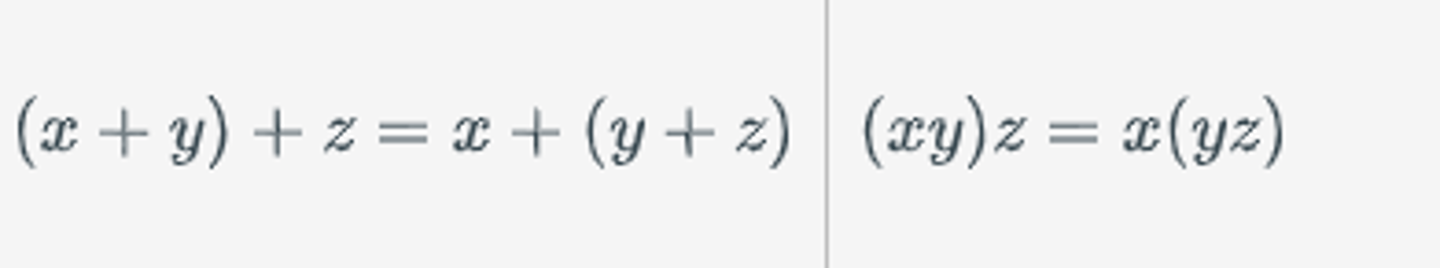
Commutative laws (Boolean algebra)

Rearranging the values will not change the truth value.

Complement laws (Boolean algebra)

Addition or multiplication by the complement will equal either the multiplicative or additive identity value. Also, the complement of 1 is zero, and the complement of 0 is one.

De Morgan's laws (Boolean algebra)

The complement of an OR expression is the same as an AND statement of their individual complements. The complement of an AND statement is the same as an OR statement of their individual complements.

Distributive laws (Boolean algebra)

Addition can be distributed to each factor; multiplication can be distributed to each term.

Domination laws (Boolean algebra)

Multiplication by the additive identity, 0, equals 0. Addition by the multiplicative identity, 1, equals 1.

Double complement law (Boolean algebra)

A double negative makes a positive.

Idempotent laws (Boolean algebra)

To say x OR x—or to say x AND x—is redundant. In both cases, we just have x.

Identity laws (Boolean algebra)

Addition or multiplication by the identity values of 0 and 1 respectively, does not change the original value

Literal

a single Boolean variable or its complement; for example, x¯ and x.

Minterm

the product of literals; for example, x¯yz

To find a Boolean expression that is equivalent to a Boolean function defined by an input/output table:

Each row of a table defining a Boolean function corresponds to a minterm.

Find each row where the value of f=1.

Write the expression for each row whose minterm equals 1.

Put an addition operator (+) between each expression.

The rules for disjunctive normal form DNF (the sum of products of literals):

Complements are applied to only single variables:

No addition within a term: