Engineering Materials

What are Materials

Materials are anything made up of atoms (including gases like air). Depending on conditions, a material may be in the solid, liquid, or gaseous state. The focus of engineering is to understand how these atomic building blocks and their arrangements give rise to useful properties.

What is Material Science/ Engineering

Materials Science & Engineering links structure, properties, and processing/synthesis:

• Structure at multiple scales: macro (e.g., mm, m), micro (e.g., grains, phases), and atomic (bonding and crystal arrangements).

• Properties: especially mechanical (e.g., tensile behavior measured in lab), but also electrical, thermal, magnetic, and optical.

• Processing/synthesis: ways we make and shape materials to achieve target structures and properties.

Classification of Materials

Materials may be grouped by different criteria:

• Chemical bonding: Metals (metallic), Ceramics (ionic), Polymers (co-valent).

• Electrical behavior: Insulators, Semiconductors, Conductors, Super-conductors.

• Application: Structural (selected mainly for mechanical performance), Functional (e.g., magnetic), Biomaterials.

• Grain structure/size: Single crystal; Polycrystalline; Coarse grained (> 1 μm); Ultrafine (100–1000 nm); Nanocrystalline (< 100 nm). Grain size and crystallinity significantly affect mechanical behavior.

Types of Materials: Metals (metallic bonding)

Strong and often ductile; high thermal and electrical conductivity; usually opaque and reflective

Types of Materials - Polymers/ Plastics (covalent chains, weaker secondary interactions

Soft, ductile, relatively low strength for static duty; low density; typically thermal/electrical insulators; often translucent/transparent (e.g., lightweight optical uses).

Types of Metals - Ceramics (predominantly ionic, also covalent)

Combinations of metallic and nonmetallic elements (e.g., oxides, carbides, nitrides, sulfides). Brittle, glassy, and exhibit small elastic strains; generally insulating.

Types of Metals - Composites

Engineered combinations of two or more classes (e.g., polymer + ceramic) to combine advantages that are difficult to achieve in a single material.

Structure - Processing - Properties

Properties depend on structure. (Example: hardness varies with steel microstructure.)

• Processing changes structure. Tailoring microstructure via processing enables property control.

• Design insight. Understanding the processing→structure→properties linkage is essential for effective materials design.

Materials Selection Process

1. Application → determine required properties (mechanical, electrical, thermal, magnetic, optical).

2. Match properties → identify candidate materials (structure, composition).

3. Choose processing → methods that achieve the required structure/shape (e.g., casting, sintering, vapour deposition, additive manufacturing).

Conductivity vs Strengthening

Both impurity atoms (solid solution) and plastic deformation (work hardening) strengthen metals, but they tend to reduce electrical conductivity (e.g., adding impurity atoms to Cu increases resistivity; deforming Cu also increases resistivity).

Why Mechanical Properties Matter

Mechanical properties quantify how materials respond to loads. If a structure is too soft, it deforms excessively; if it is too hard/brittle, it may not absorb energy and can fail catastrophically (or transmit dangerous loads to occupants). Design strives for a balanced response: strong enough to limit damage, yet capable of absorbing energy.

How we Evaluate Mechanical Properties

We apply controlled loads and observe responses:

• Tension: Most common method; yields full stress–strain behavior.

• Compression: Used when service involves compression or when tension would cause brittle failure.

• Torsion: A form of pure shear; useful for shear properties.

Engineering Stress and Strain

To remove specimen-size effects, we normalize force and deformation:

σ = F/Ao

, ε = ∆l/lo

Elastic Deformation (Reversible)

Elastic deformation stretches atomic bonds; when the load is removed, atoms return to equilibrium. Elasticity can be linear or nonlinear. In the linear regime,

Hooke’s law holds:

σ = E ε,

with E the modulus of elasticity (Young’s modulus), i.e., the slope of the initial linear part of the stress–strain curve (stiffness).

Nonlinear Elasticity: Tangent and Secant Moduli

Some materials (e.g., grey cast iron, concrete, many polymers) are not linearly elastic. Useful slopes include:

• Tangent modulus: instantaneous slope at a chosen stress.

• Secant modulus: slope of a straight line from the origin to a chosen point on the curve.

Bonding Forces and Stiffness

Between neighboring atoms, there is both an attractive force (bonding) and a repulsive force (electron cloud overlap). The net force is their sum; at equilibrium spacing the net force is zero (maximum stability). Young’s modulus reflects the resistance to changes in this spacing. As temperature increases, E generally decreases (bonds soften), typically monotonically but not strictly linearly with T .

Anelasticity (Time-Dependent Elasticity)

• Elastic deformation: reversible, immediate (bond stretching).

• Anelastic deformation: reversible but time-dependent recovery after unloading (a delayed elastic return).

• Plastic deformation: permanent (e.g., via shear of atomic planes).

Poisson’s Ratio and Moduli Relations

A specimen stretched axially also changes laterally. Poisson’s ratio is

ν = − εlateral/ εaxial

.

For isotropic solids, the elastic constants are interrelated (Young’s, shear, and bulk moduli with ν).

Plastic (Permanent) Deformation

Once yielding begins, unloading follows a line parallel to the elastic loading line; the recovered portion is the elastic part. Further elastic deformation continues even during the plastic region (the curve’s slope during unloading equals the

original E).

Yield Strength (0.2% Offset Method)

Yield strength is the stress at which noticeable plastic strain begins. On the engineering curve, draw a line parallel to the initial linear portion but starting at ε = 0.002; the intersection defines σy .

Tensile Strength (UTS)

Maximum engineering stress. In metals this is usually where necking begins; in polymers it can coincide with chain alignment prior to break.

Ductility

Plastic tensile strain at failure (how much it stretches before fracture).

Toughness

Energy absorbed before fracture (area under the stress–strain curve). Brittle fracture is mainly elastic energy; ductile fracture includes substantial plastic energy.

Resilience

Elastic energy stored up to yield; the modulus of resilience is the strain energy per unit volume up to σy .

True Stress and Strain (Concept)

As a specimen elongates, its instantaneous cross-section shrinks. True measures use instantaneous area/length. Before necking, uniform deformation allows meaningful interpretation; after necking, deformation localizes and simple uniform formulas cease to represent the whole gauge section meaningfully.

Work Hardening and Elastic Strain Recovery

Plastic deformation can raise the flow stress (work hardening). Unloading from the plastic regime recovers the elastic portion along a straight line of slope E. Reloading causes yielding to resume near the prior maximum stress (raised yield point). Work hardening increases the difficulty of dislocation motion and is a key strengthening mechanism. If work hardening capability is insufficient, deformation localizes (necking) and ductility suffers.

Hardness: Meaning and Measurement

Hardness is resistance to permanent surface indentation. A harder material resists plastic deformation and compressive cracking, and often exhibits better wear resistance. Hardness testing is:

• Simple and inexpensive, with small (nondestructive) indentations,

• Correlatable to other properties (empirical conversions),

• High spatial resolution, enabling linkage to local microstructure (especially with nanoindentation).

Variability, Statistics and Safety Factors

Critical properties can vary due to flaws and processing history. Use statis-

tics (e.g., mean, standard deviation) and design/safety factors to account for

uncertainties:

• Uncertain service stresses,

• Property variability,

• Manufacturing imperfections,

• In-service damage accumulation.

Equations: Engineering Stress

Explanation: Load divided by original area Ao

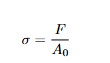
Equations: Engineering Strain

Explanation: Change in length relative to the original length lo

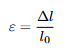
Equations: Engineering shear strain

Explanation: Lateral shift ∆x per thickness y

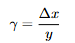
Equations: Linear Elasticity (Hooke’s Law)

Explanation: E is the slope of the initial stress-strain curve (stiffness)

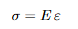
Equations: Poisson’s ratio

Explanation: Lateral construction relative to axial extension

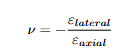
Equations: Isotropic relations linking Young’s Modulus, shear and bulk moduli via poissons ratio

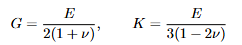
Offset Strain

Explanation: 0.2% offset strain used to define the yield strength σy on the engineering curve

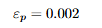
Equations: Modulus of resilience

Explanation: Elastic energy density up to yield

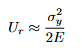
Equations: True Stress and Strain

Explanation: Uses instantaneous area Ai and current length li

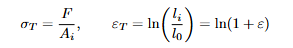
Equations: Link between true and engineering stress measures whilst deformation is uniform

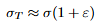
Equations: Work hardening (plastic flow) law

Explanation: K and n from the true curve

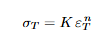
Empirical conversion between tensile strength and Brinell hardness

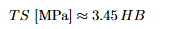
Safety/design factors to allow for load and properly variability

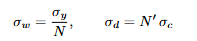
Ceramics: Elastic and Brittle at Room temperature

Ceramics (ionic/covalent) typically show linear elasticity up to brittle failure. Tensile tests are challenging; three-point bending is commonly used to obtain stiffness and strength measures. Flexural strength depends on specimen size (larger volumes have a higher probability of critical flaws).

Noncrystalline Ceramics (glasses): Viscous Flow

Glasses deform by viscous flow (akin to liquids). The deformation rate is proportional to applied stress. Viscosity quantifies resistance to flow; high viscosity corresponds to strong interatomic adhesion and difficulty of deformation.

Polymers: Three Archetypal Stress-Strain behaviors

Polymer response is highly sensitive to strain rate, temperature, and the chemical environment. Three common behaviors:

1. Brittle: elastic then fracture (small strains).

2. Plastic: elastic region followed by permanent (often large) plastic deformation.

3. Elastomeric: totally elastic with very large, recoverable strain at low stress (elastomers).

Basic mechanical quantities for polymers are defined similarly to metals (modulus from the initial slope; yield strength at the end of the elastic region; tensile strength at fracture).

Temperature and Strain-rate Effects (Thermoplastics)

Both metals and polymers are affected by temperature and strain rate, but polymers are more sensitive. Higher temperatures and/or lower strain rates generally make polymers softer and more ductile; lower temperatures and/or higher rates promote brittleness.

Tensile Response Details

Unlike metals (where post-necking deformation localizes mainly in the neck), polymers can distribute deformation differently. In semi-crystalline polymers, plasticity typically proceeds in stages:

1. Elongation of the amorphous regions,

2. Alignment of crystalline regions,

3. Sliding of crystalline regions.

For elastomers, compare to other polymers: aligned, crosslinked networks can show a brittle-like response at low temperature or high rate, whereas semicrystalline polymers show the plastic sequence above.

Viscoelastic Deformation and Relaxation

Amorphous polymers:

• Behave like glasses at low temperature (Hooke’s law valid at small strains),

• Behave like viscous liquids at high temperature,

• Show rubbery (viscoelastic) behavior in between.

Viscoelastic response depends on both time and temperature. In a stress relaxation test (rapidly strain to a small, fixed strain and hold), the recorded stress decays over time; the relaxation modulus Er (t) captures this decay.

Glass Transition Temperature (Tg)

• Crystalline materials: sharp solid–liquid transition with a discontinuous change in density at melting.

• Amorphous materials (glasses): continuous change in density with temperature, but a change in slope at a characteristic temperature Tg . Below Tg the material is rigid/glassy; above Tg it is rubbery/viscous.

Different polymers exhibit different Er (t) vs temperature behaviors: nearly fully crystalline polymers show little decrease at Tg ; highly cross-linked polymers show a rubbery plateau (useful region for elastomers); amorphous polymers show a more pronounced drop at Tg .

Equations: Three-point bending - Elastic modulus E

For a simply supported beam of span L with a central load F and mid-span deflection: (image)

Meaning: Ceramics are brittle in tension, so bending is used to obtain E.

F is the applied mid-span load, δ the mid-span deflection at that load, b × d the

rectangular cross-section, R the radius for circular cross-sections.

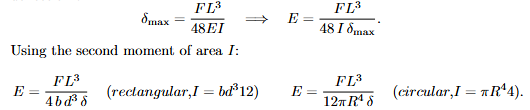
Equations: Flexural Strength (failure in bending)

At failure load Ff , the maximum bending moment is Mmax = Ff L/4. With c the outer-fibre distance and I the second moment:

Meaning. Ceramics are brittle in tension, so bending is used to obtain E. F is the applied mid-span load, δ the mid-span deflection at that load, b × d the rectangular cross-section, R the radius for circular cross-sections.

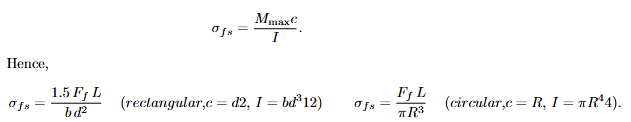
Glass; viscous flow (amorphous ceramics)

Meaning. Glasses deform by viscous flow. The viscosity η measures resistance to shear-driven deformation; larger η in your notes indicates more difficult deformation (strong interatomic adhesion).

Viscoelastic stress relaxation (polymers)

Meaning. In the stress-relaxation test described in your notes, the specimen is rapidly strained to a small fixed strain ε0 and held. The measured stress σ(t) decays with time; the relaxation modulus Er (t) captures this decay and its strong dependence on temperature and loading time/rate (glassy → rubbery → viscous regimes).

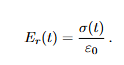
Variable Definitions

What is a composite

A composite is an artificially made multiphase material designed to achieve property combinations unattainable in a single phase (principle of combined action). Combining distinct phases can yield lighter, stronger, and more corrosion-resistant structures.

Terminology and Phases

• Matrix (continuous phase): carries and redistributes load, protects the reinforcement, and often supplies toughness/ductility. Matrix types include MMC (metal), CMC (ceramic), PMC (polymer).

• Dispersed phase: embedded within the matrix and tailored (particle, fibre, structural forms) to enhance targeted properties.

Spatial/geometric characteristics of the dispersed phase (size, shape, distribution, orientation, continuity) strongly influence properties.

Classification Overview

• Particle-reinforced: large-particle or dispersion-strengthened (10–100 nm), with different strengthening mechanisms.

• Fibre-reinforced: continuous (aligned) or discontinuous (aligned/random).

• Structural: laminates and sandwich constructions.

Particle Reinforced Composites

Large-particle composites: Particle–matrix interactions follow continuum mechanics; particles are often equiaxed.

Dispersion-strengthened composites: Nano-scale dispersions (10–100 nm) hinder deformation at the atomic level (analogous in spirit to precipitation strengthening), and remain effective at higher temperatures.

Concrete and Reinforcement Concepts

• Plain concrete (gravel + sand + cement + water) is strong in compression but very brittle in tension.

• Reinforced concrete uses steel rods, wires, bars, or meshes to increase strength; even if concrete cracks, the steel carries tension.

• Prestressed concrete: bars/mesh are tensioned during setting; releasing tension after setting places concrete in compression, so external tensile stress must first overcome this compressive state to crack.

• Post-tensioning: tightening after curing achieves a similar compressive bias.

Fibre-Reinforced Composites

Why fibres? Fibres are very strong in tension and can dramatically increase composite strength and stiffness (e.g., fibreglass: continuous glass filaments in a polymer matrix).

Fibre types

• Whiskers: thin single crystals with very high length/diameter ratios (e.g., graphite, Si3N4, SiC); extremely strong but expensive and difficult to disperse.

• Fibres: polycrystalline or amorphous (e.g., alumina, aramid); usually polymers or ceramics.

• Wires: metals (e.g., steel, tungsten); used in tires, rocket casings, etc.

Matrix role and interface

The (softer) matrix binds fibres, transfers load, provides ductility, and prevents crack propagation between fibres. Strong adhesive bonding at the fibre–matrix interface is crucial to minimize fibre pull-out and to maximize tensile strength.

Stress Position and Alignment Effects

Load sharing between matrix and fibres depends on position and fibre alignment. Aligned fibres provide anisotropic stiffness/strength; random orientations reduce peak anisotropy but also reduce directional performance.

Composite stiffness and Strength (Qualitative)

Longitudinal loading (continuous fibres): fibres and matrix strain

together; the composite modulus is high when Vf and fibre stiffness are high.

• Transverse loading (continuous fibres): fibres carry less load; stiff-

ness is lower than in the longitudinal direction.

• Tensile strengths: in the longitudinal case, fibre fracture marks the

onset of failure; in the transverse case, reinforcement may be less effective. Strength depends on fibre/matrix properties, interface quality, and void

Failure of fibre-reinforced composites is often not catastrophic: fibres do not all fail simultaneously, and the matrix can continue to carry reduced loads, allowing some residual capability.

Production Methods

Pultrusion: Continuous fibres are pulled through a resin bath, then a pre-forming die shapes them, and a heated die cures the thermosetting resin into accurate profiles.

Filament winding: Resin-impregnated fibres are wound in controlled patterns onto a mandrel (often cylindrical); curing occurs in an oven or at room temperature; the mandrel is then removed.

Structural composites: Laminates are stacked/bonded fibre-reinforced sheets with chosen stacking sequences (e.g., 0◦/90◦) to tailor in-plane properties