Chapter 8 Notes: Truth Tables (Symbolic Logic)

truth functions

the truth value of any compound statement (in propositional logic) is a function of the truth values assigned to its SIMPLE COMPONENTS

simple components

the simple statements within the compound statements

main operator

The truth value can be assigned to the _____ of more complex statements if you know the truth value of its simple constituents. 

truth table

a table that shows us the TRUTH VALUE of a compound statement under EVERY POSSIBLE ASSIGNMENT of TRUTH VALUES to the SIMPLE COMPONENT

truth table definition of a conjunction

truth table definition of a disjunction

truth table definition of a negation

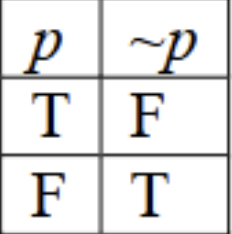
truth table definition of a conditional

truth table definition of a biconditional

1. List the premises and the conclusion in one horizontal line (conclusion on the far right).

   1. Separate the premises from the conclusion with a double slash. 

2. Determine the number of rows by using 2ⁿ, where n is the number of different letters in the symbolized argument. 

3. Start filling in truth values under each letter.

   1. Divide the TOTAL number of lines in half. Then go to the LEFTMOST LETTER and fill in that number of Ts and then that number of Fs. Do this every time you see this letter.

   2. Divide the number you just used in half again, go to the next leftmost letter and fill in that number of Ts and number of Fs. Do this everywhere you see that letter.

   3. Continue until your last letter; you’re alternating T, F, T, F all the way down the table everywhere you see that letter.

4. Fill in the truth values for the operators IN EACH PREMISE and for the CONCLUSION using truth table definitions. If the statement is COMPOUND, you will fill in the main operator last. 

5. Check to see whether there’s any line on which the truth value under the main operator (or letter) of EACH PREMISE is T and the truth value under the main operator (or letter) of the CONCLUSION is false.

   1. If there IS such a line, the argument is INVALID.

   2. If there IS NOT such a line, the argument is VALID.

Steps for testing arguments with truth tables:

double slash

What do we use to separate the premises from the conclusion in a truth table?

single slash

What do we use to separate the premises from each other in a truth table?

2ⁿ, where n = the number of DIFFERENT letters in symbolized argument

How do you determine the number of rows in a truth table?

1. Divide the TOTAL number of lines in half. Then go to the LEFTMOST LETTER and fill in that number of Ts and then that number of Fs. Do this every time you see this letter.

2. Divide the number you just used in half again, go to the next leftmost letter and fill in that number of Ts and number of Fs. Do this everywhere you see that letter.

3. Continue until your last letter; you’re alternating T, F, T, F all the way down the table everywhere you see that letter.

How do you determine the truth values of the letters in truth tables?

indirect truth table

shortcut to direct truth tables that involves:

• Assigning the value “T” to the MAIN OPERATOR of EVERY PREMISE

• Assigning the value “F” to the MAIN OPERATOR of the CONCLUSION

• Filling in the rest of the values for the letters and operators

  • If an argument is VALID, trying to make the premises true and conclusion false should result in a CONTRADICTION

  • No contradiction = INVALID

contradiction (indirect truth tables)

assigning T and F to the same simple statement at different places (indirect truth tables)

1. Tautalogous

2. Self-contradiction

3. Contingent

3 types of classifying statements

tautalogous

a compound statement that turns out to be TRUE NO MATTER WHAT TRUTH VALUES are assigned to its SIMPLE COMPONENTS

the value under the statement’s main operatoris TRUE on EVERY LINE

truth table terms for tautalogous statements

self-contradictory

a statement that turns out to be FALSE NO MATTER WHAT TRUTH VALUES are assigned to the SIMPLE COMPONENTS

the value under the statement’s main operator is FALSE on EVERY line

truth table terms for self-contradictory statements

contingent

a statement that is TRUE under AT LEAST ONE assignment of truth values to its SIMPLE COMPONENTS AND it’s FALSE under AT LEAST ONE

the value under the main operator (or single letter) is TRUE on AT LEAST ONE line AND FALSE on AT LEAST ONE

truth table terms for a contingent statement

• Fill in the column under the statement’s MAIN OPERATOR LAST

• Fill in the values under other operators (after letters) depending on what are the main operators of other parts of the statement

The order to follow when filling out a truth table (compound statements)

1. Logically Equivalent

2. Contradictory

3. Consistent

4. Inconsistent

Four Relations

logically equivalent

a type of relation in which two statements NECESSARILY have the SAME TRUTH VALUE

same truth value under the main operators on every line

truth table terms for logically equivalent relation

contradictory

a type of relation in which two statements NECESSARILY have OPPOSITE truth values

opposite truth values on every line under their main operators

truth table terms for a contradictory relation

consistent

a type of relation in which it’s POSSIBLE for both statements to be TRUE at the SAME TIME 

on AT LEAST ONE line, the value TRUE appears under the main operator of BOTH STATEMENTS

truth table terms for a consistent relation

inconsistent

a type of relation in which it’s IMPOSSIBLE for both statements to be TRUE at the SAME TIME

NO LINE on which TRUE appears under the main operator of BOTH STATEMENTS

truth table terms for inconsistent relation

TWO statements CONTRADICT, ONE statement can be SELF-CONTRADICTORY

How are contradiction and self-contradiction different?

True

• statements can have more than one of these relations to each other

True or False: the 4 relations we defined are NOT mutually exclusive

inconsistent

Any statements that contradict each other must also be _______

False

• Statements CAN be logically equivalent to each other without stating the same information in two different ways.

True or False: Statements can only be logically equivalent if they restate the same information in two different ways.

logically equivalent

All tautologies are ________ ______ even though they don’t all state the same thing.

self-contradictory

All __________ statements are logically equivalent to one another.

strongest

Statements with multiple relations are usually classified by the _________ relation.

logically equivalent statements

If two statements are logically equivalent adn consistent, they are classified as

contradictory statements

If two statements are contradictory and inconsistent, they are classified as