Ch9: Clustering

What is clustering in data mining?

A: An unsupervised learning method used to automatically group data points into clusters based on similarity, without using labeled data.

What are common use cases of clustering?

A:

• Organizing documents

• Customer segmentation

• Web search result grouping

• Image segmentation

• Shopping pattern discovery

How is an instance typically represented in clustering?

A: As a point in n-dimensional space:

x=⟨ a₁(x),a₂(x),...,a_n(x) ⟩

What is a common distance metric for measuring similarity in clustering?

Euclidean distance, defined as:

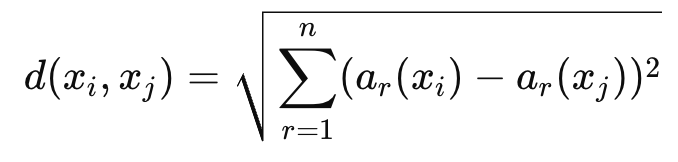
What is the K-means clustering algorithm?

A: An iterative algorithm that partitions data into K clusters by minimizing the distance between data points and their assigned cluster centroids.

What are the steps of the K-means algorithm?

A:

1. Initialize K cluster centers

2. Assign each point to the nearest cluster

3. Update each cluster center to be the mean of its assigned points

4. Repeat steps 2–3 until assignments no longer change

What does K-means minimize during training?

A: The sum of squared distances from each data point to its assigned cluster center (within-cluster variance).

Is K-means guaranteed to converge?

A: Yes — it converges in a finite number of steps, though not necessarily to a global optimum.

What is the computational complexity(running time) of K-means?

A:

• O(k⋅n) for assigning points to clusters

• O(n) for updating cluster means

What distance properties must the similarity measure satisfy?

A:

1. Symmetry: D(A,B)=D(B,A)

2. Positivity: D(A,B)>0 and D(A,B)=0 if A=B

3. Triangle inequality: D(A,C)≤D(A,B)+D(B,C)

How is the number of clusters K determined?

A:

• It is not well defined and often problem-dependent.

• A common heuristic: look for a "kink" or elbow in the objective function graph

What are the main advantages of K-means clustering?

A:

• Simple and intuitive

• Efficient on large datasets

• Guaranteed to converge

What are the main disadvantages of K-means?

A:

• Sensitive to outliers and noise

• Struggles with non-circular (non-convex) clusters

• May converge to local optimum

• Requires pre-specifying K