SIMPLE HARMONIC MOTION TO REMEMBER

SHM

An object's motion is simple harmonic, when the acceleration is proportional to the displacement, and always in the opposite direction to the displacement.

Displacement

The displacement of an oscillating particle is its distance and direction from the equilibrium position.

Amplitude

The maximum displacement of an oscillating particle.

Time period

The time for one complete cycle of oscillation

Frequency

The number of cycles per second made by an oscillating object.

Angular frequency, ⍵

⍵ = 2πf

Phase difference

The difference in phase between two oscillating objects. It is usually expressed in fractions of a cycle or radians.

Phase difference in radians = 2πΔt/T

Free oscillations

An object oscillates at its own natural frequency. A free oscillation may be undamped or damped.

Damped oscillations

Oscillations are damped if dissipative forces are present. The oscillator's amplitude decreases due to a damping force acting in the opposite direction to the velocity.

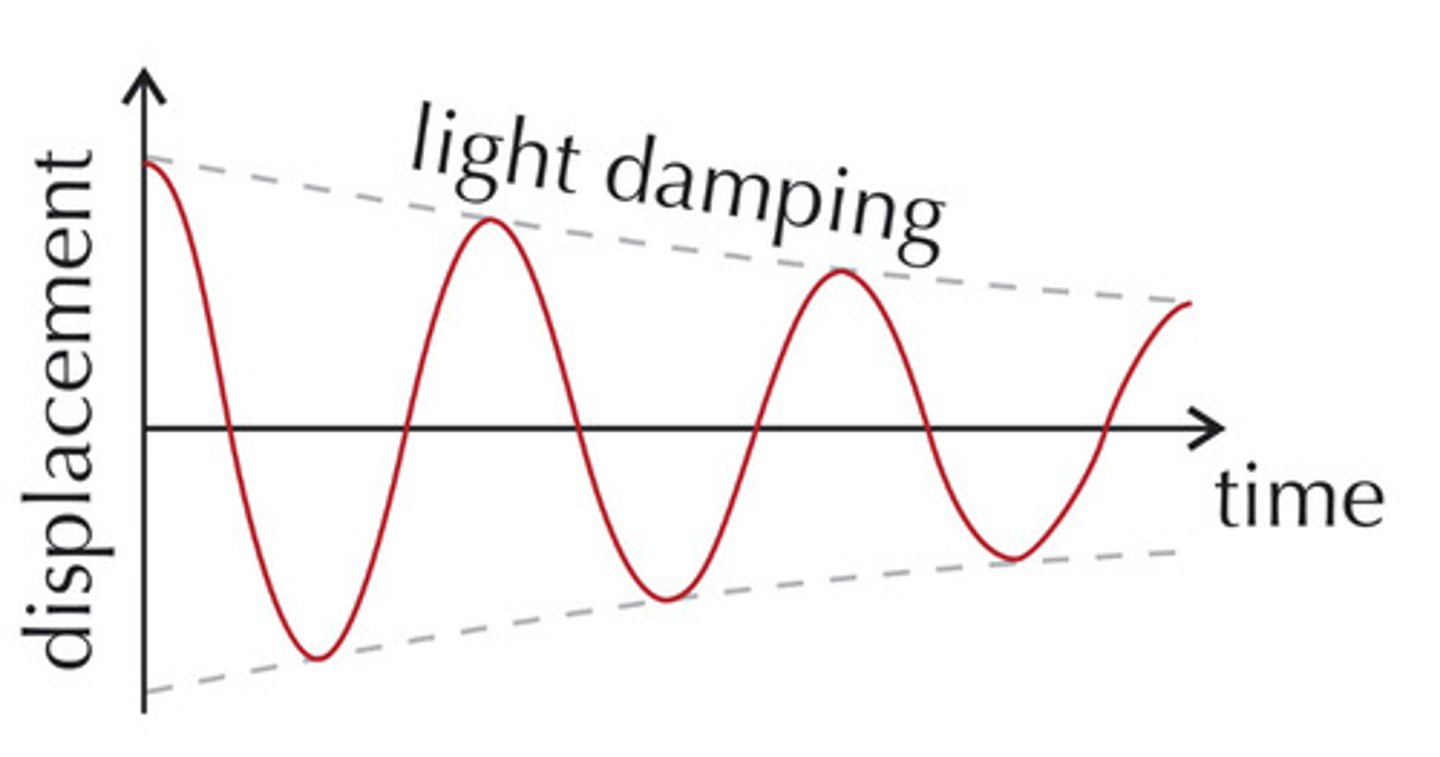
Light damping

The time period is independent of the amplitude so the amplitude of the oscillations steadily decreases while each cycle takes the same amount of time.

- decays exponentially w/ time

Critical damping

The oscillating system returns to equilibrium in the shortest time possible, without overshooting.

Heavy damping

The damping is so strong that the displaced object returns to equilibrium slowly, without any oscillation.

Forced oscillations

A periodic force is applied to the system. The response depends on the frequency of the periodic force (and how it compares with the natural frequency of the oscillating system).

Resonance

When the frequency of the applied force to an oscillating system is equal to its natural frequency, the amplitude of the resulting oscillations increases significantly

- at this point, the system will be transferring the maximum kinetic energy possible

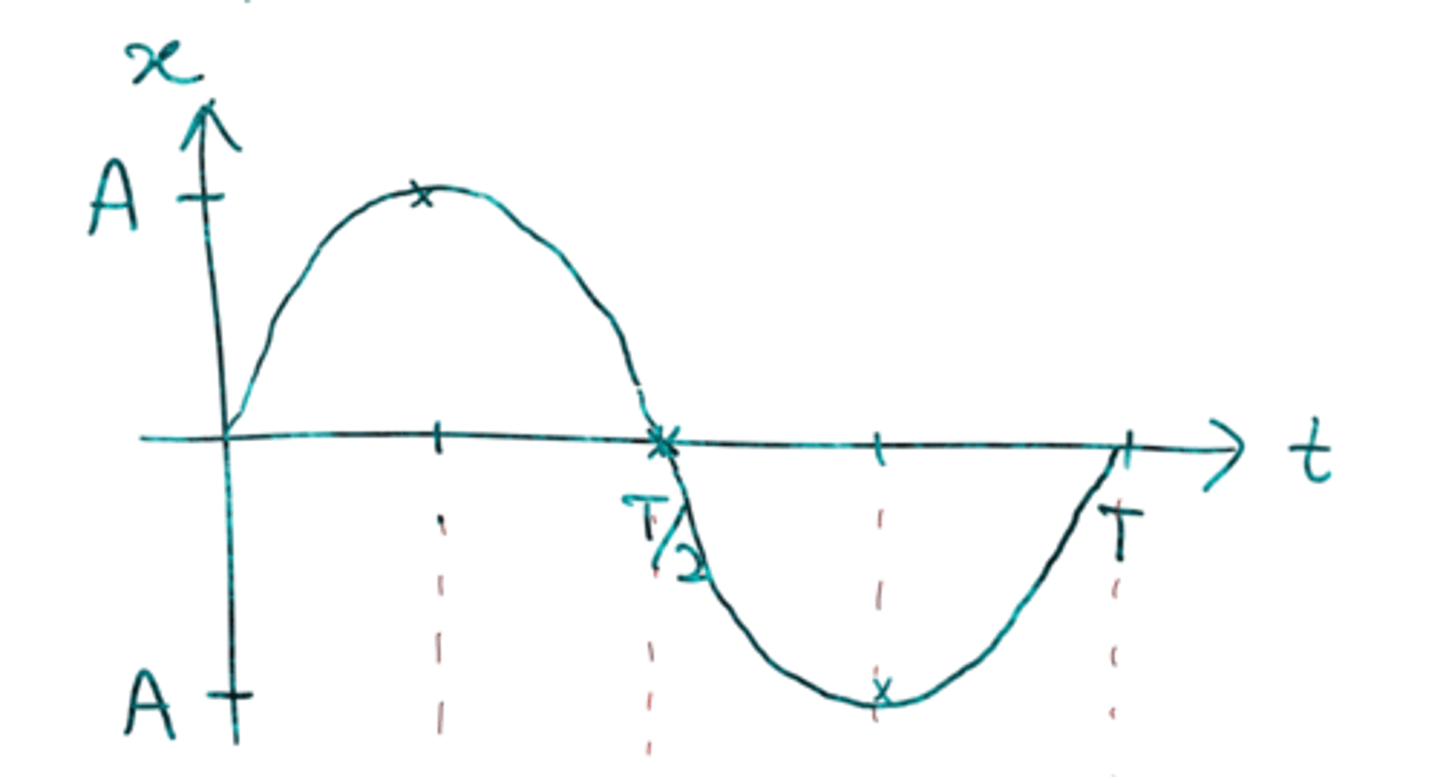
Displacement (m) against time (second) graph

Sin wave

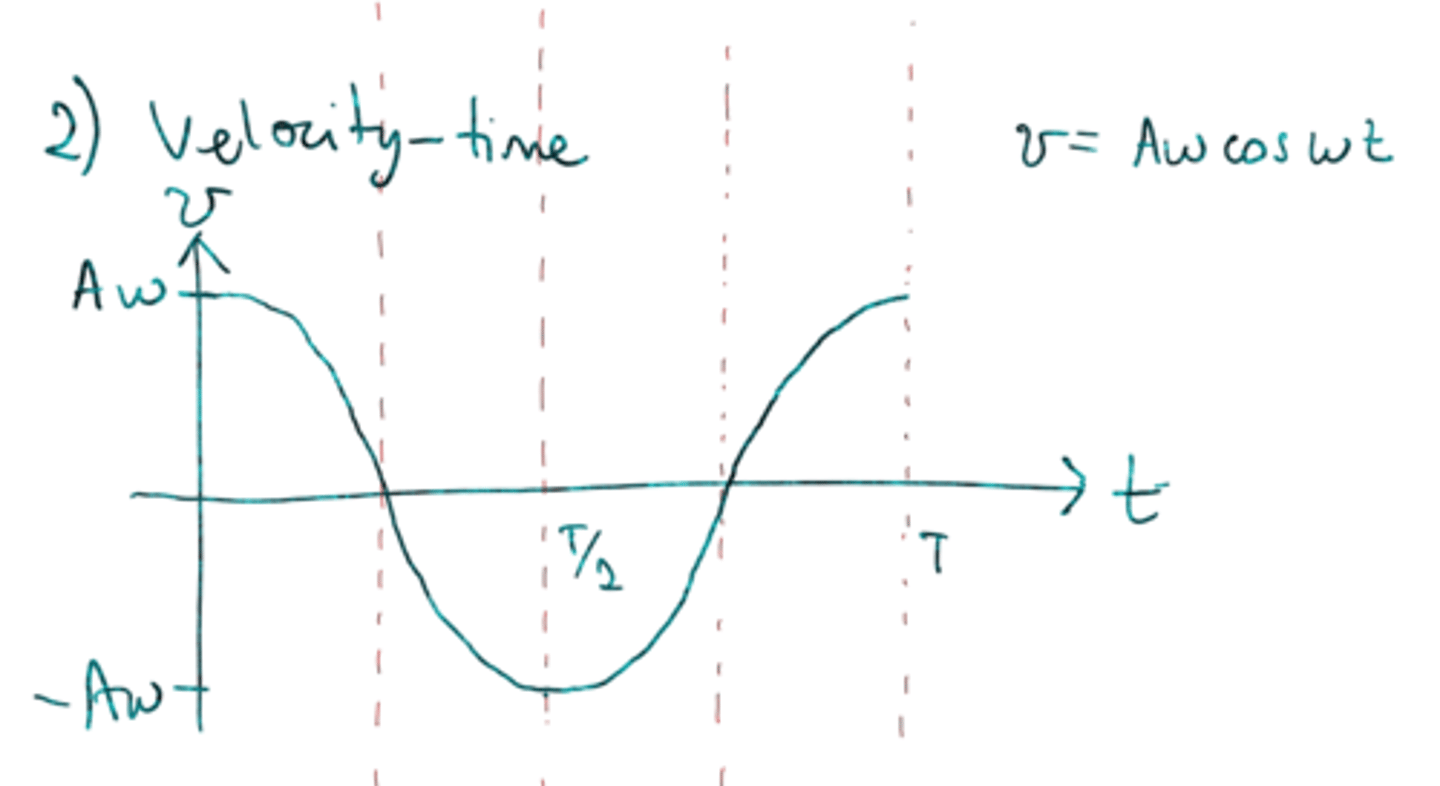
Velocity (ms⁻¹) against time (second) graph

Cos graph

- because the greatest velocity is at equilibrium

- V-t graph is 90° out of phase

(vel is the rate of change of 𝔁 ∴ gradient)

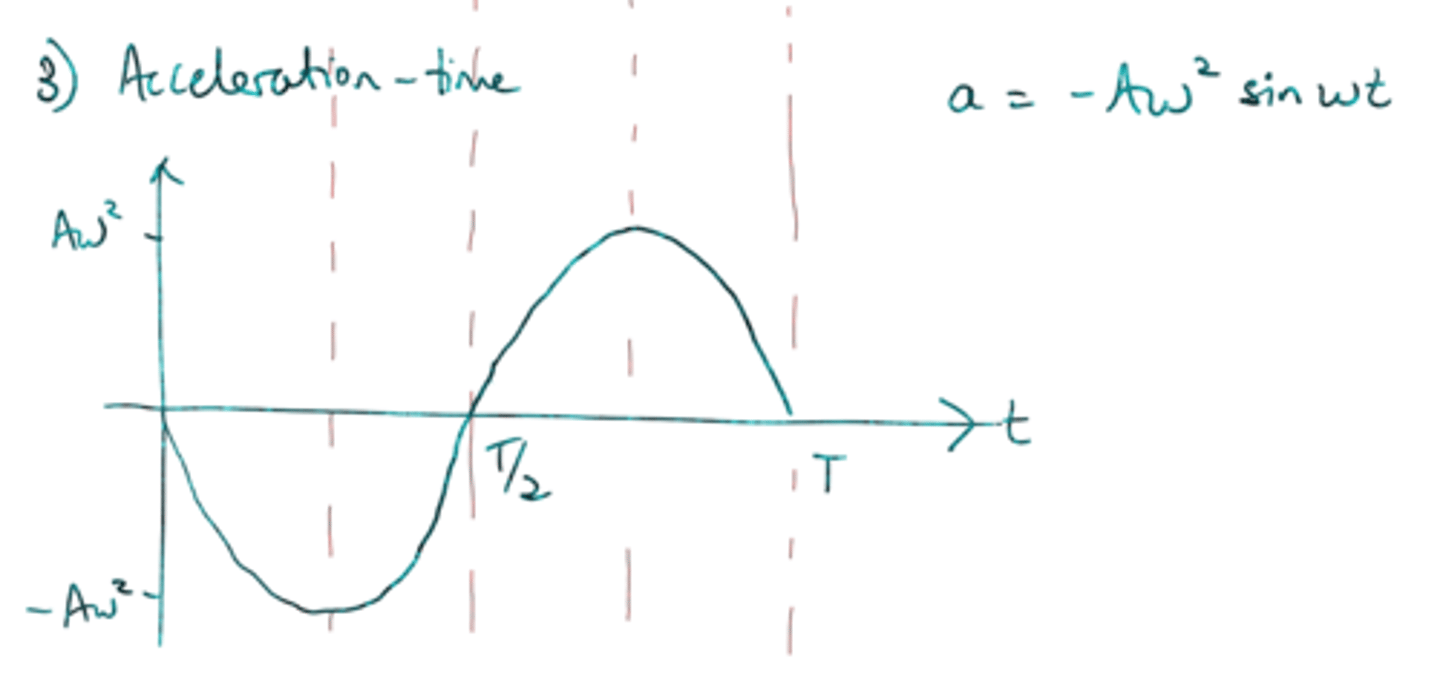
Acceleration (ms⁻²) against time (second) graph

Sin graph

a=-⍵²𝔁

F=-k𝔁 & F=ma

a=-𝔁

so basically its the 𝔁 vs t graph but the inverse bc its negative 𝔁

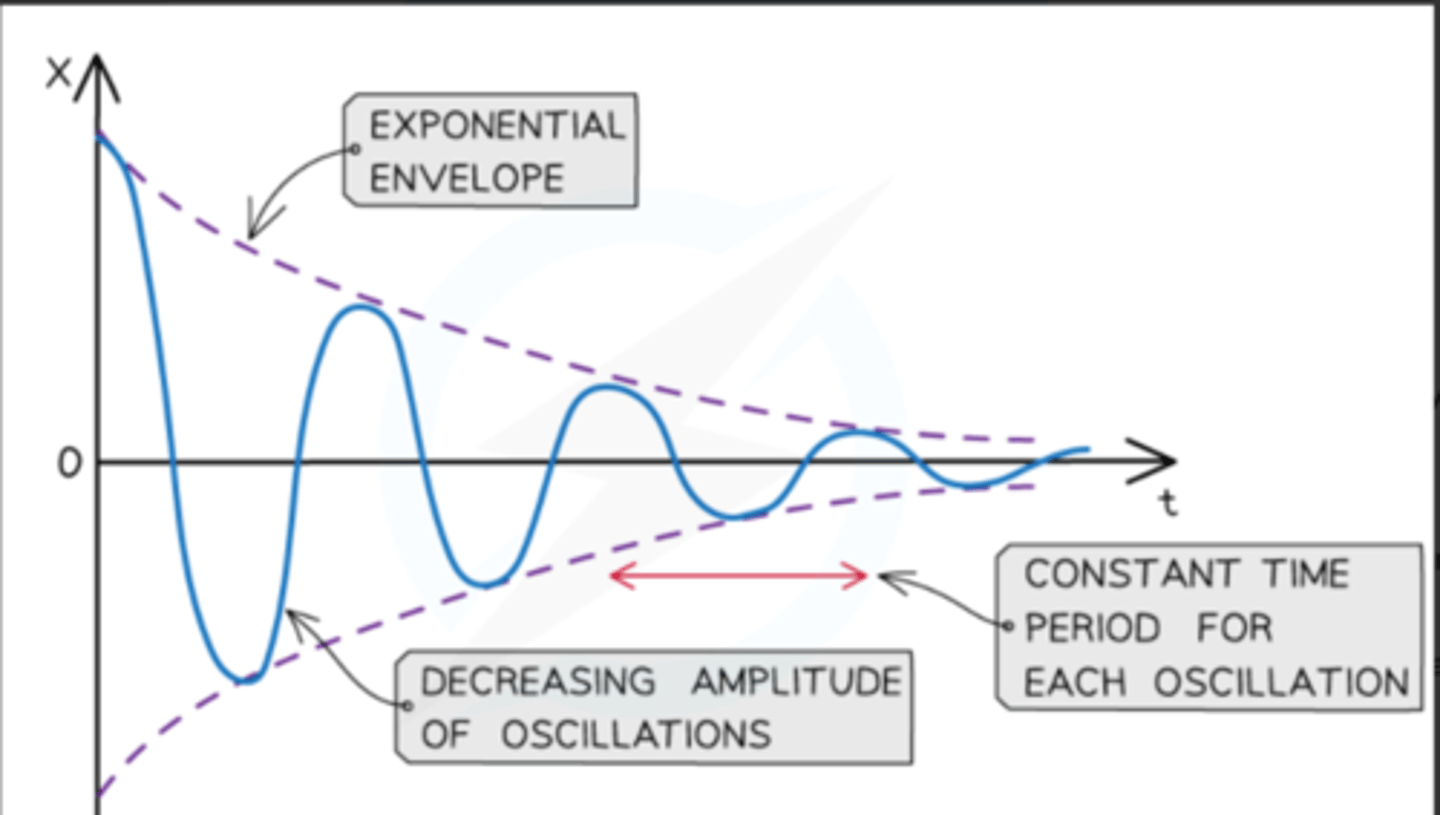
Key features of a lightly damped system

- There are many oscillations represented by a sine or cosine curve with gradually decreasing amplitude over time

- The amplitude decreases exponentially

- The frequency of the oscillations remain constant, this means the time period of oscillations must stay the same and each peak and trough is equally spaced

Key features of a critically damped system

- This system does not oscillate, meaning the displacement falls to 0 straight away

- The graph has a fast decreasing gradient when the oscillator is first displaced until it reaches the x axis

- When the oscillator reaches the equilibrium position (x = 0), the graph is a horizontal line at x = 0 for the remaining time

Key features of a heavily damped system

- There are no oscillations. This means the displacement does not pass zero

- The graph has a slow decreasing gradient from when the oscillator is first displaced until it reaches the x axis

- The oscillator reaches the equilibrium position (x = 0) after a long period of time, after which the graph remains a horizontal line for the remaining time

The Effects of Damping on Resonance

Damping reduced the sharpness of resonance and reduces the amplitude at resonant frequency

- the resonance peak broadens

- the resonance peak moves slightly to the left of the natural frequency when heavily damped

- has no effect on the f₀

Amplitude against f₀ graph

When f < f0, the amplitude of oscillations increases

At the peak where f = f0, the amplitude is at its maximum. This is resonance

When f > f0, the amplitude of oscillations starts to decrease

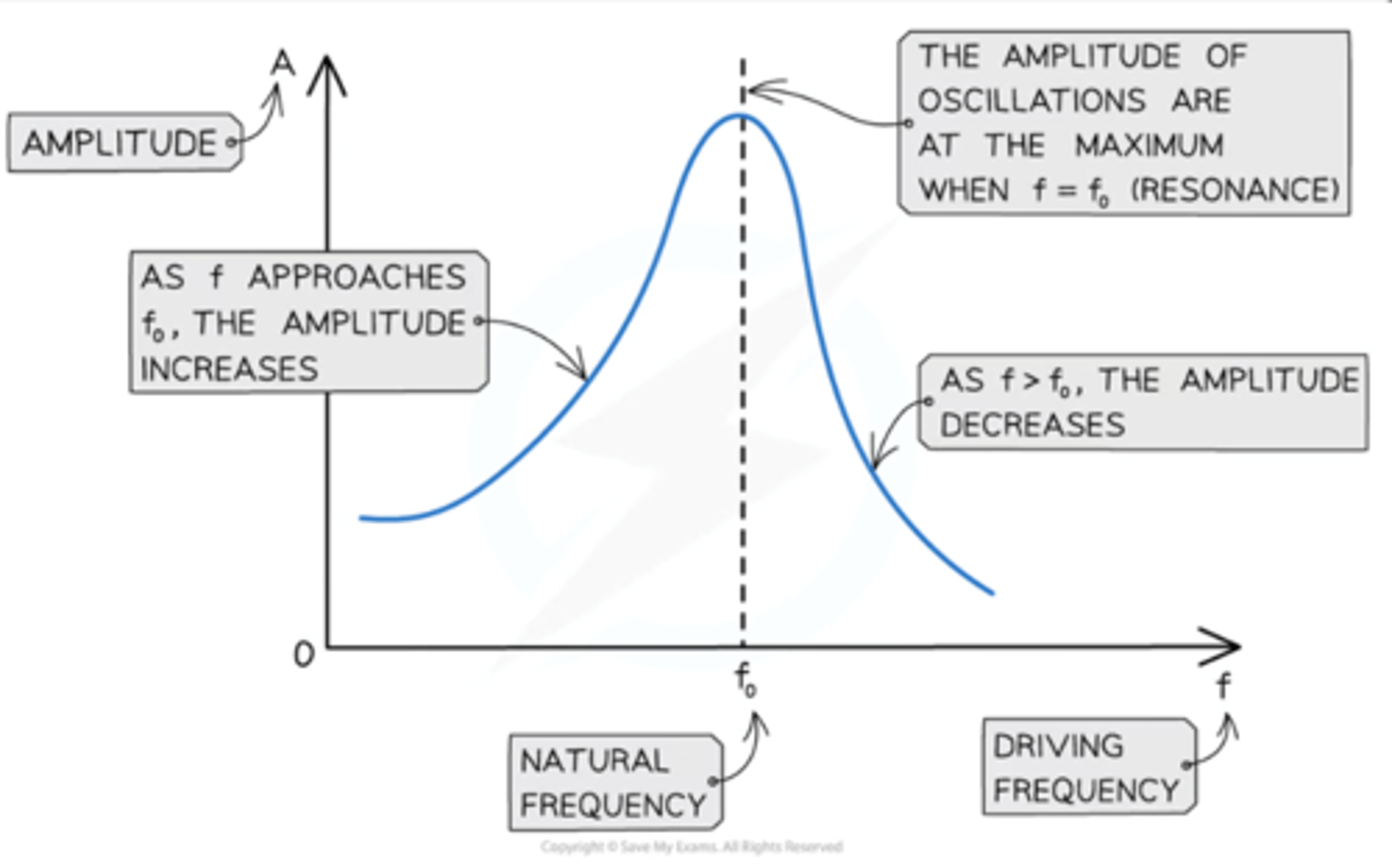
Natural frequency (f₀)

The frequency of an oscillation when the oscillating system is allowed to oscillate freely

Driving frequency

The frequency of forced oscillations

OR

The frequency of the applied force

Examples of resonance effects

An organ pipe, where air resonates down an air column setting up a stationary wave in the pipe

Glass smashing from a high pitched sound wave at the right frequency

A radio tuned so that the electric circuit resonates at the same frequency as the specific broadcast

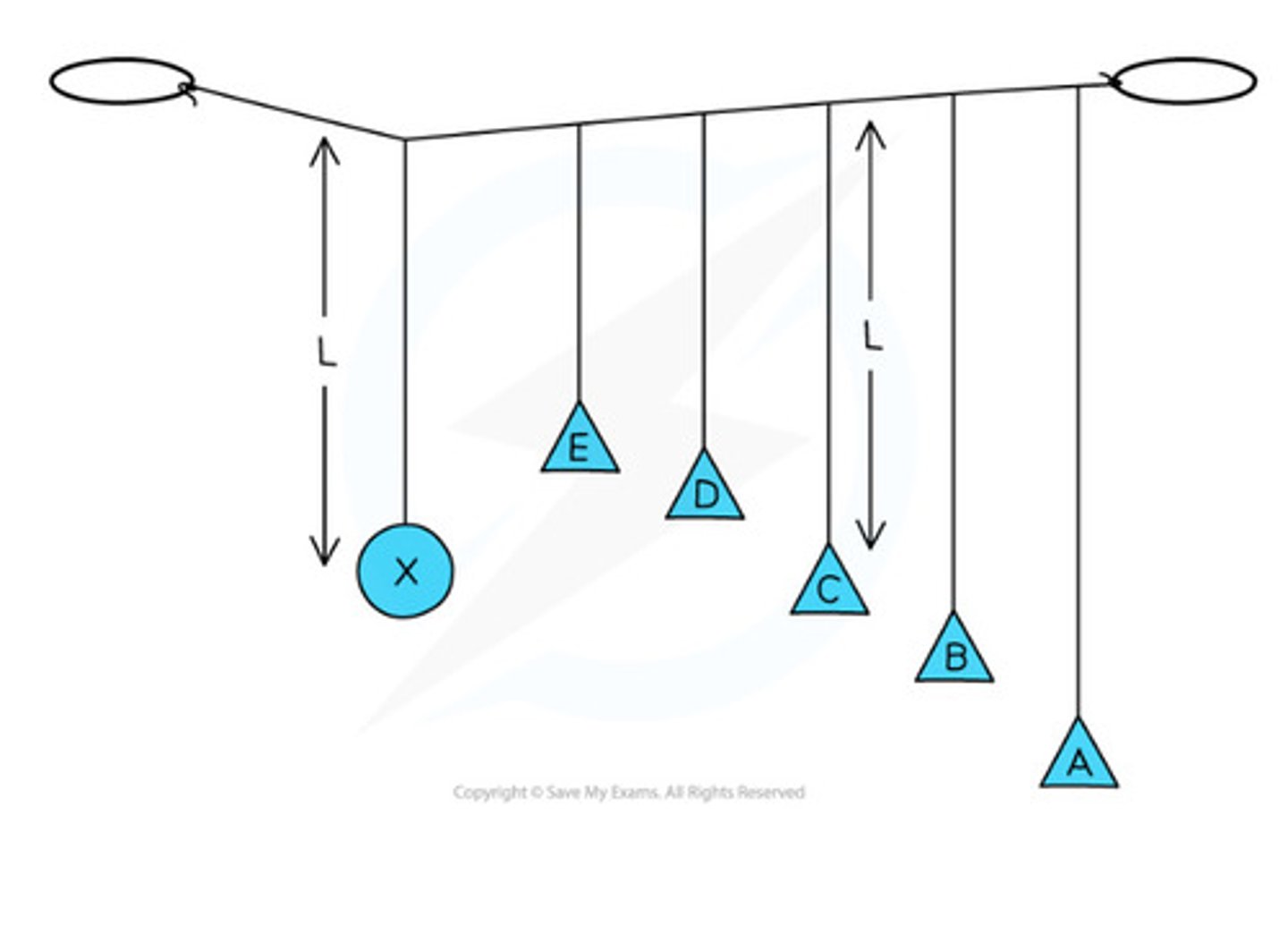
Barton's pendulums

Most strings swing with a low amplitude but pendulum C with the same length L has the largest amplitude

- bc f₀ = f(pendulum)

The phase of the oscillations relative to the driver are:

- pendulums E and D with lengths < L are in phase

- pendulum C with length = L is 0.5π out of phase

- pendulums B and A with lengths > L are π out of phase