4: electronic spectroscopy & photochemistry

describe observable differences between atomic and molecular spectroscopy

atomic = lines observed in spectra

molecular = bands observed in spectra

define spectroscopy

investigation and measurement of spectra produced when matter interacts with or emits electromagnetic radiation (light)

describe absorption in atomic spectroscopy

there are discrete atomic energy levels. a transition from the ground state to the excited state can be initiated by incident light of the exact energy/wavelength. this can give information on the size of the energy gap and position of energy levels.

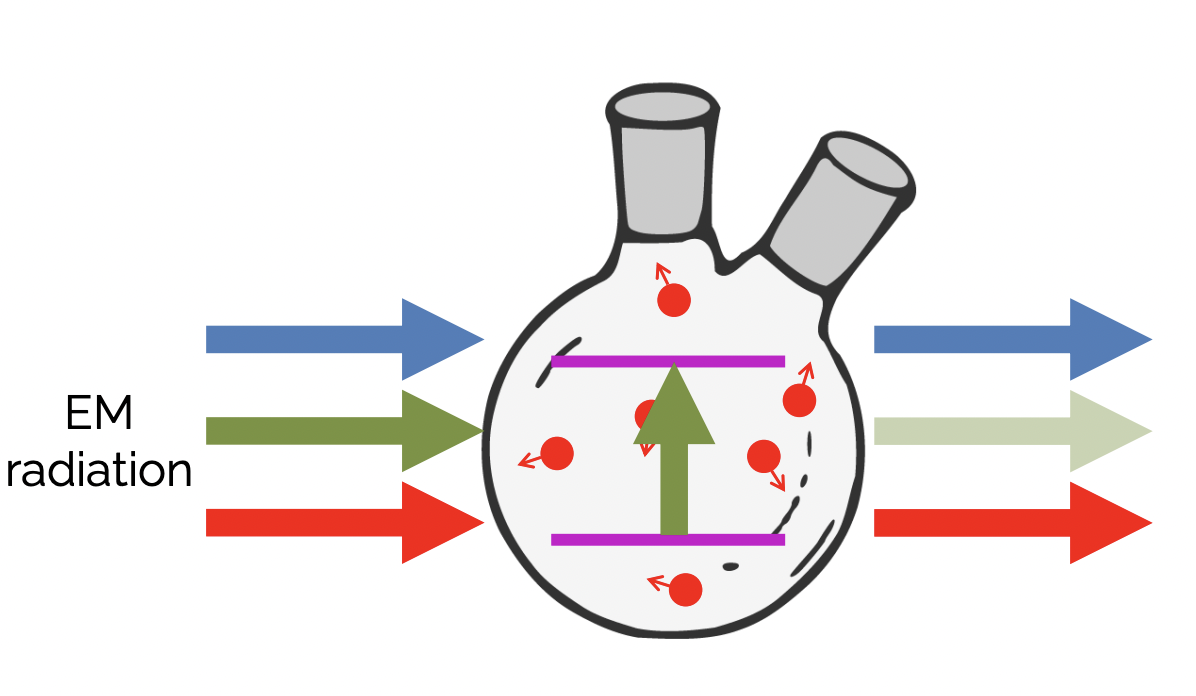
describe emission in atomic spectroscopy

there are discrete atomic energy levels. relaxation of matter from excited state to ground state emits light of the exact energy/wavelength of transition. this can give information on the size of the energy gap and position of energy levels.

define laser light

• highly focused = beam

• monochromatic = all same wavelength

• coherent = all in phase

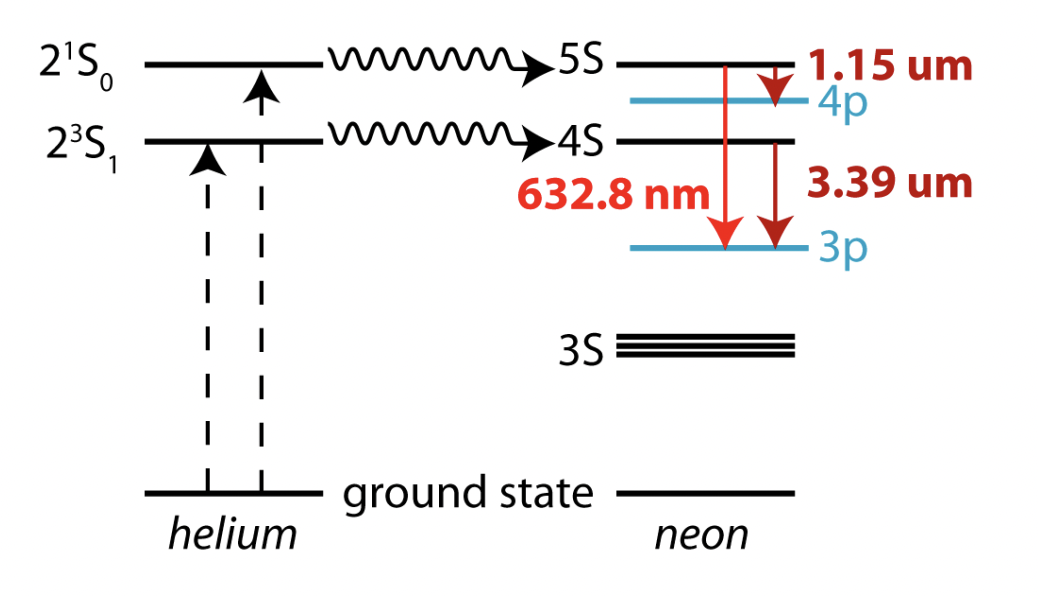
describe a possible basis for a laser

helium-neon gas mixture

helium atom is excited. this energy is transferred to a neighbouring neon atom through collisional energy transfer. this excites electrons in the neon atom. relaxation of these electrons to lower energy level emits a photon. this gives red light which is:

• monochromatic = all same wavelength

• coherent = all in phase

describe molecular spectroscopy

as opposed to atomic orbitals, transition occur between molecular orbitals.

what processes occur on the femtosecond timescale?

• bond formation and breakage

• chemical reactions

• isomerisation

• molecule relaxation

what different units can be used to depict energies and transitions?

• wavenumber (v~)

• electron volt (eV)

describe eV

e = charge of an electron = 1.6×10(-19)

divide the energy by e to yield the energy in eV

= energy gained across a potential difference of 1 volt

what is a simple method to convert from wavelength to eV?

*WAVELENGTH MUST BE IN nm*

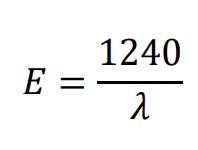
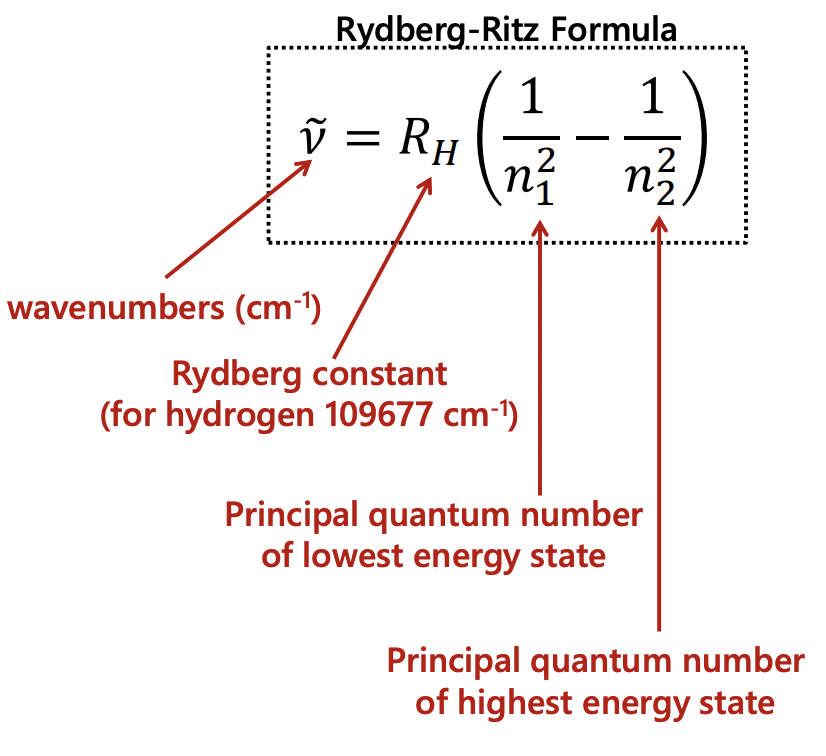
describe the Rydberg-Ritz formula

= for hydrogen = atomic

gives the wavelengths/frequencies of the spectral lines/transitions in atomic emission between quantised energy levels of the hydrogen atom

what is the Rydberg-Ritz formula?

describe the different types of transitions described by the Rydberg-Ritz formula

dependent on where the electron transition ends = lower energy level defines which series

Lyman: transition to n=1

Balmer: transition to n=2

Paschen: transition to n=3

Brackett: transition to n=4

LBPB

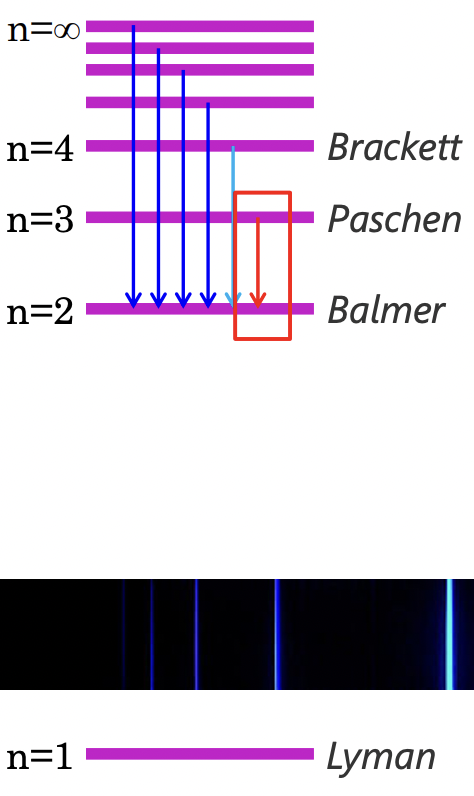
how is each transition of each type of transition defined?

nth Lyman/Balmer/Paschen?Brackett line

n = number of energy levels removed from where transition ends

i.e. 1st Lyman line: n=2 → n=1

2nd Lyman line: n=3 → n=1

1st Balmer line: n=3 → n=2

2nd Balmer line: n=4 → n=2

how does energy and wavelength vary by nth X line?

1st = smallest energy gap = largest wavelength

energy gap will increase = wavelength will decrease

describe the Balmer lines

all the transitions (nth Balmer lines) have wavelengths within the visible region

determine the wavelength of the third line in the lyman series in eV

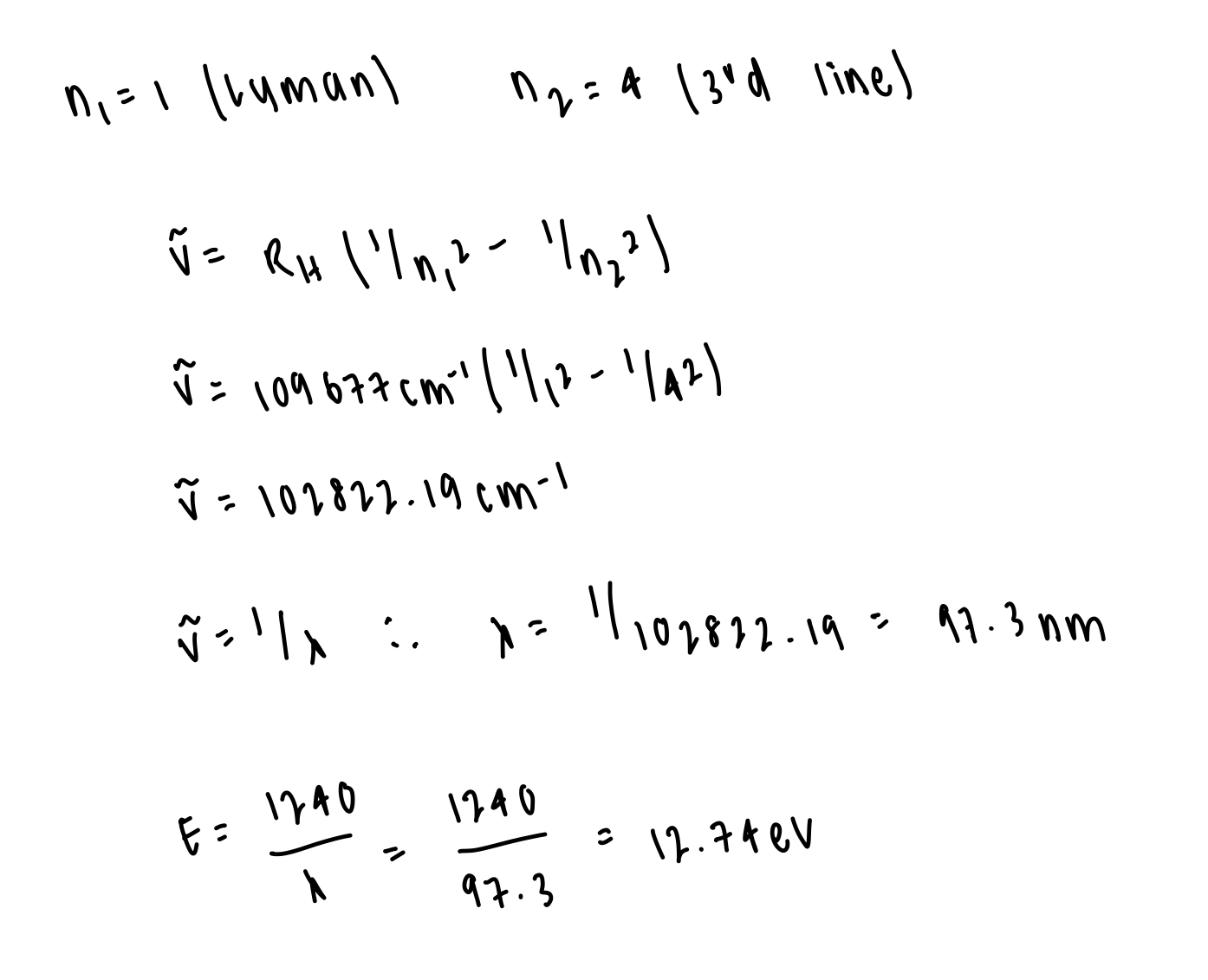
describe quantum number l

= orbital angular momentum quantum number

= different sub-shells that an electron can occupy (s, p, d) have different geometry and have different boundary conditions of the Schrodinger equation

what values can l take for each value of n? what geometries correspond to each value of l?

l = 0, 1, 2, …, (n-1)

n possible values of l for each value of n

l = 0: s

l = 1: p

l = 2: d

l = 3: f

degenerate

describe quantum number m(l)

= magnetic quantum number

= while l describes the shape of the orbital, m(l) describes the orientation of the orbitals

= the z-component of l

what values can m(l) take for each value of l?

m(l) = -l, -l+1, …, +l

2l+1 possible values of m(l) for each value of l

degenerate states

what happens to the electron states upon application of a magnetic field?

the m(l) substates lose their degeneracy

(since different orientations of orbitals will interact differently with magnetic field)

what are the selection rules for electron transitions in atomic spectrocopy?

• Δl = +/- 1

• Δm(l) = 0 or +/- 1

arise from conservation of angular momentum, considering photon itself has angular momentum

how can the energies of energy states in hydrogen be determined?

(in P1 section of equation sheet)

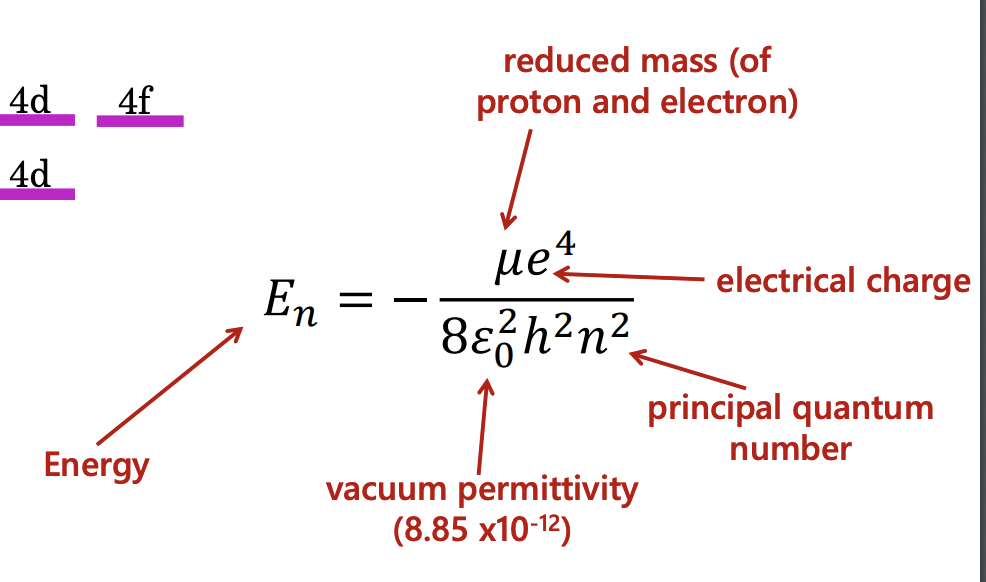
why is l not included in the energy state equation?

hydrogen is a single electron system

= energy determine only be the distance of the electron from the nucleus (Coulomb potential)

= energy NOT determined by the shape or orientation of the orbitals

this is not the same of multi-electron atoms

determine the energy level of n=1 in hydrogen atom

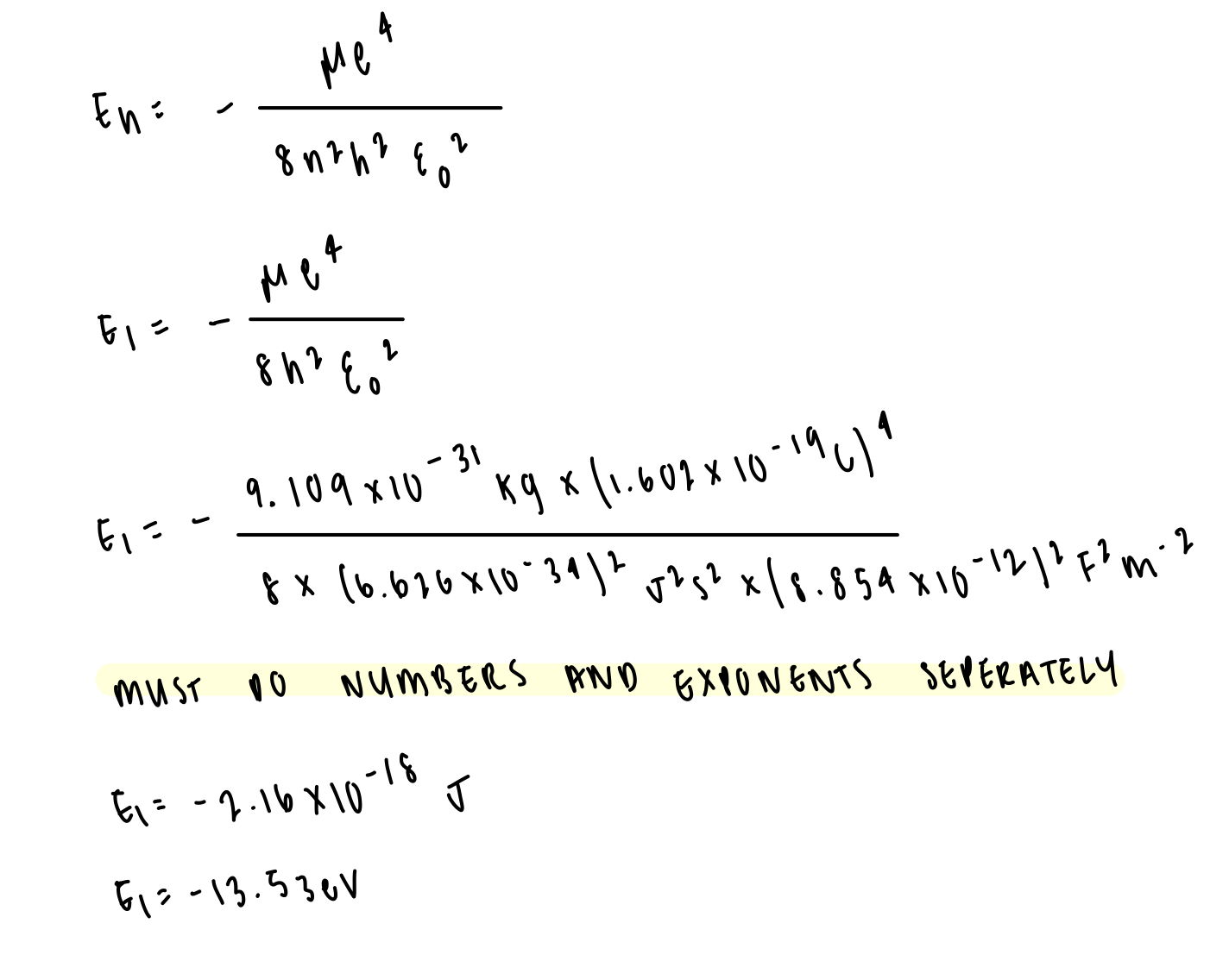
determine the energy level of n=3 in hydrogen atom

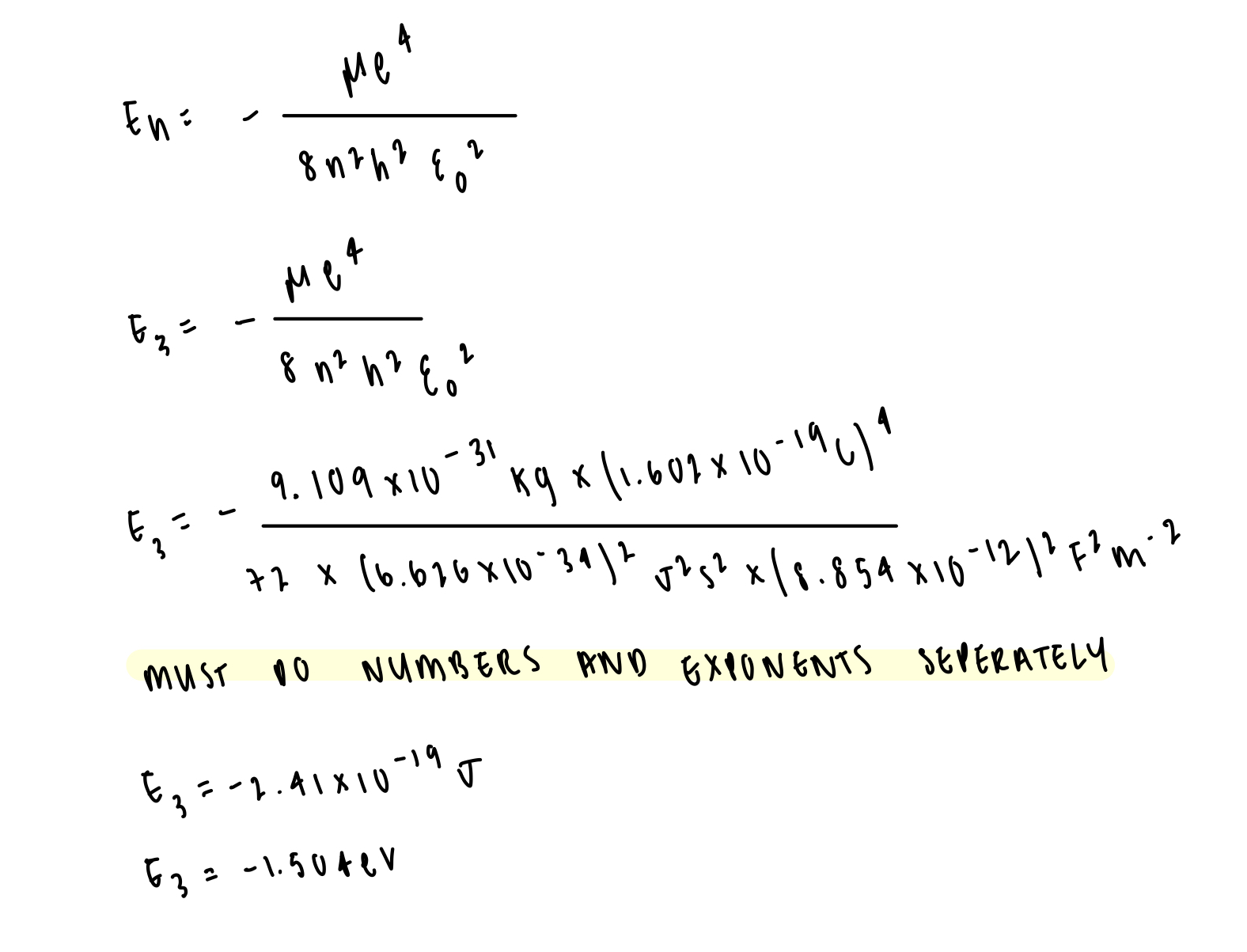
determine the size of the energy gap between n=3 and n=1 in hydrogen atom

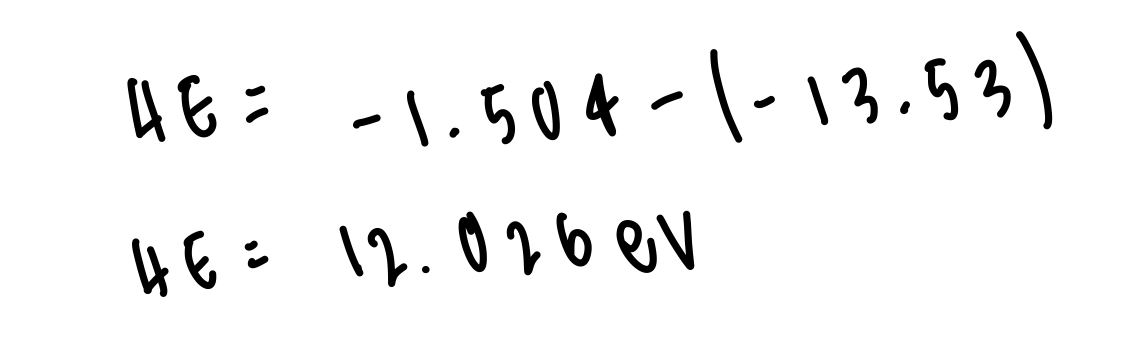
describe absorption/emission transitions in many electron atoms

single electron transitions

many transition observed for many electron atoms are typically one electron movement between orbitals, while the others generally remain in their initial states

i.e.

how does the atomic orbital diagram differ from hydrogen for many electron atoms?

the degeneracy of orbitals with the same value of n but different value of l is broken

why is the degeneracy of orbitals broken in many electron atoms?

• spin-orbit coupling

• relativistic effects

• external fields

• penetration

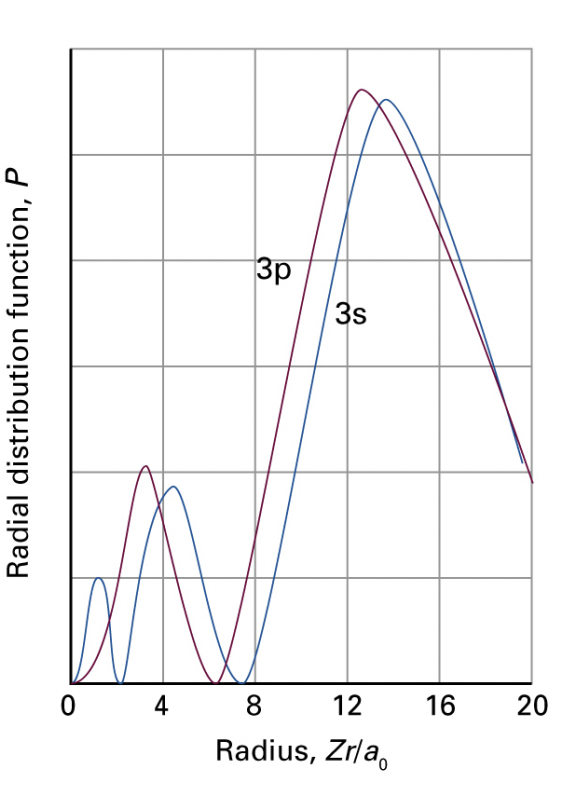
describe penetration

atoms from lithium (Z=3) and higher, there filled shells that should cancel some charge from the nucleus and ‘shield’ the outer electrons

however, the spatial probability distribution of outer electrons leaves some distribution close to the nucleus. this give rise to penetration and a larger effective nuclear charge.

greater nuclear charge = lower energy

lower values of l have greater penetrations = greater effective nuclear charge = lower energy

describe the relative energies of different values of l in many-electron atoms

energy: high values of l > low values of l

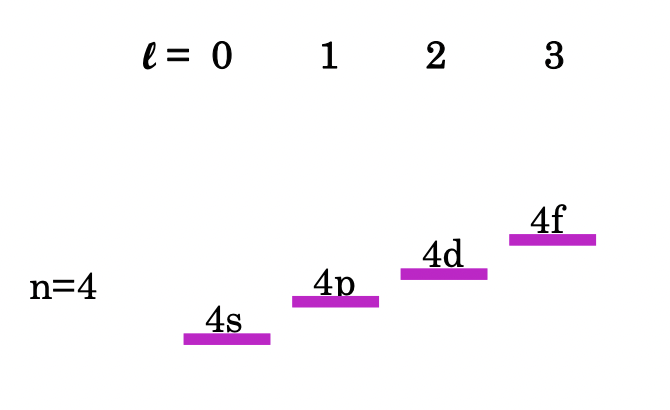
why does the Schrodinger equation not hold for many electron atoms?

interactions between electrons is to complex to be accounted for in the Schrodinger equation

what is Hund’s rule

= maximum multiplicity

= electrons will maximise spins in state = fill degenerate orbitals before coupling

what is the Pauli exclusion principle?

no two electrons can have the exact same quantum numbers

= two electrons occupying the same orbital must have opposite spins

describe quantum number s

= spin quantum number

= every electron has s = 1/2

describe quantum number m(s)

= magnetic spin quantum number

= while s describes the spin, m(s) describes the orientation of the spin

= z-component of s

= can be represented as a vector

what values can m(s) take for each value of s?

m(s) = -s, -s+1, …, +s

for electrons where s = ½

m(s) = +1/2, -1/2

what is the multiplicity of spin states

the number of different possible spin orientation combinations in a particular electronic configuration

multiplicity = 2S + 1

what is big S in the multiplicity equation?

= total spin

= sum of the m(s) values for an electronic configuration

what are the two multiplicities possible for an electron state

• triplet

• singlet

describe the triplet state

occurs when 2 electrons are unpaired

2 unpaired electrons in the ground state have the same m(s) (Hund’s rule).

hence,

S = +1/2 + +1/2 = 1

multiplicity = 2(1/2) + 1 = 3

2 unpaired electrons can have the same m(s), opposite m(s), or opposing m(s). summing the vector quantities gives 3 possible m(s) values.

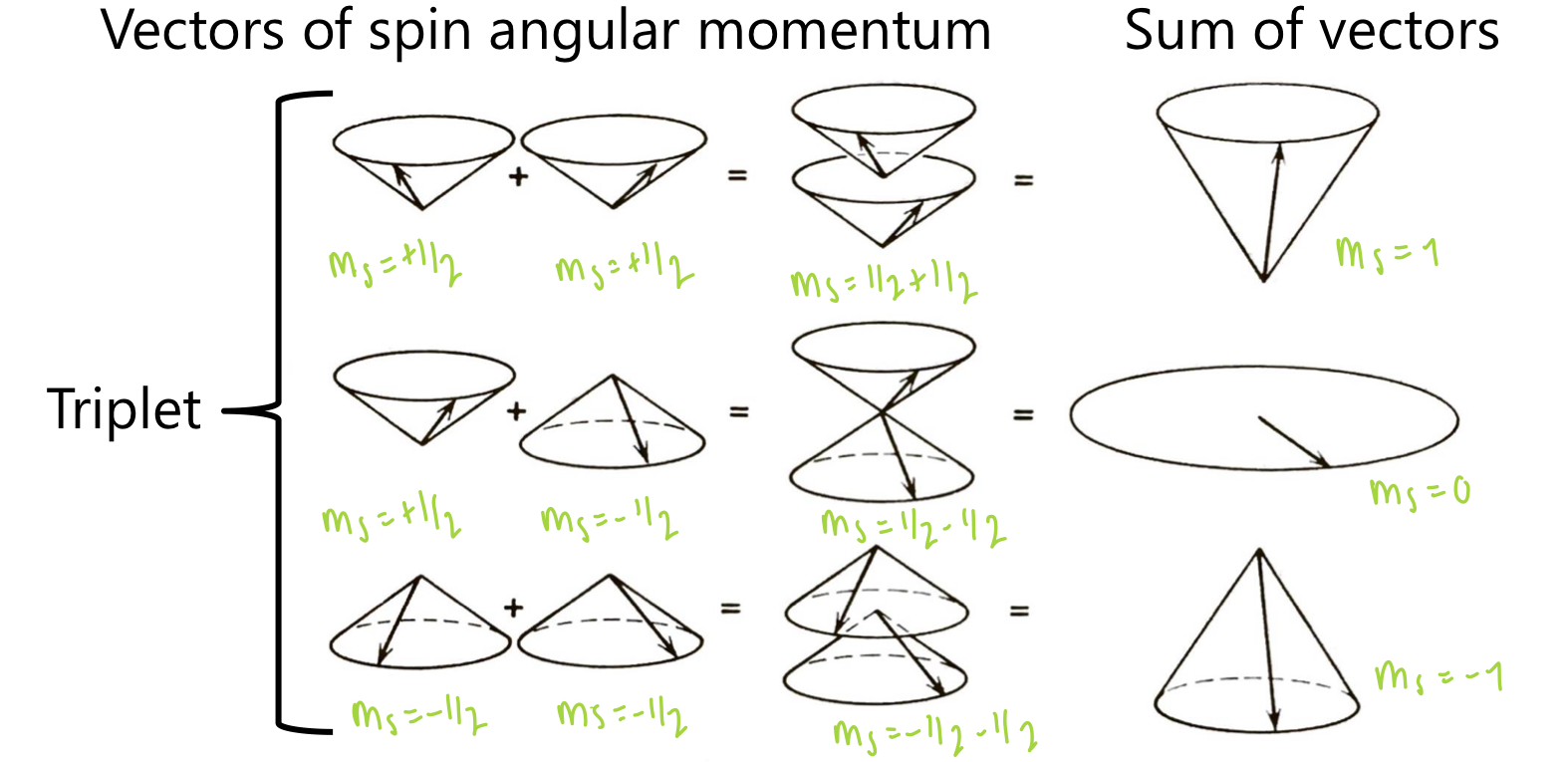
describe the singlet state

occurs when 2 electrons are paired

2 paired electrons in the ground state have opposing m(s) (Pauli exclusion principle).

hence,

S = +1/2 + (- 1/2) = 0

multiplicity = 2(0) + 1 = 1

2 paired electrons have only have opposing spins. summing the vector quantities gives only 1 possible m(s) value.

describe the decay of triplet states

the Pauli exclusion principle excludes the decay of triplet states to singlet states as a spin forbidden transition

poor to no light emission from this transition

compare spin and orbital angular momentum

spin angular momentum (s)

= rotation of the electron itself

orbital angular momentum (l)

= rotation of the electron around a point (nucleus)

describe the relative directions of spin and orbital angular momentum

spins can either be parallel or anti-parallel (vary by spin angular momentum direction ±1/2)

describe spin-orbit coupling/LS coupling/Russell-Saunders coupling

the total angular momentum can be described by quantum number j

j is the sum of spin (s) and orbital (l) quantum numbers

upon application of external field anti-parallel to l:

higher j = more resistance to external field = high E

lower j = less resistance to external field = low E

this changes the effect of the external field depending on m(s) and breaks the degeneracy of m(s) states upon application of an external field

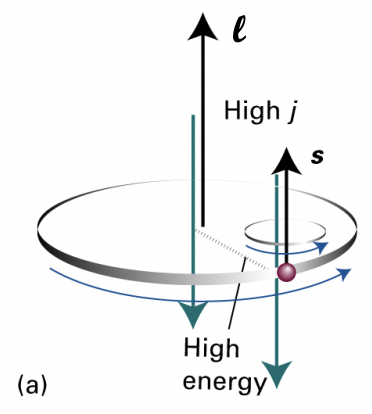
describe the value of j with the value of s

s = -1/2: anti-parallel: low j = LOWER ENERGY SUBSTATE

s = +1/2: parallel: high j = HIGHER ENERGY SUBSTATE

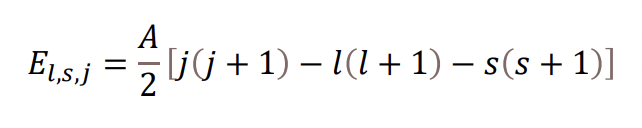
what is this equation describing and what is A?

the energy levels of substates due to spin-orbit coupling

A = spin-orbit coupling constant

A ∝ Z^4

the extent of SO splitting is much more significant for larger atoms

what effect does SO splitting have on the energy level diagram

each l state is split by SO coupling

each SO coupled substate is split by m(s)

what are term symbols?

describe the possible states for an electronic configuration

what term is used for each state?

describes only the possible configurations of 2 unpaired electrons

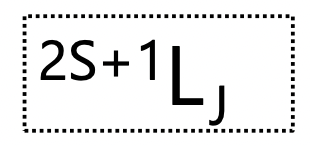
in what case is the term (1)S used?

closed shells

closed shells do not contribute angular momentum

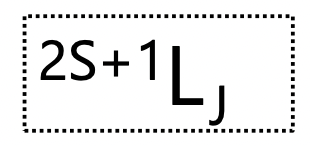
what is the ‘big L’ in the term

for two non-equivalent electrons in an unfilled outer shell

l1, l2 = l values of the configuration = can be the same OR different

(in case of 1 unpaired electrons: l1 = X, l2 = 0)

this will produce a series of L values giving the term symbols

L = 0: S

L = 1: P

L = 2: D

L = 3: F

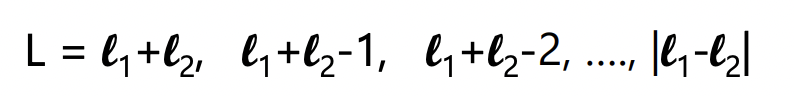
what is the ‘big S’ in the term

this yields two ~constant values:

each electron has s = ½

S = 0; S = 1

multiplicities: 1 (singlet) and 3 (triplet)

VARIES FOR SINGLE ELECTRON CONFIGURATIONS

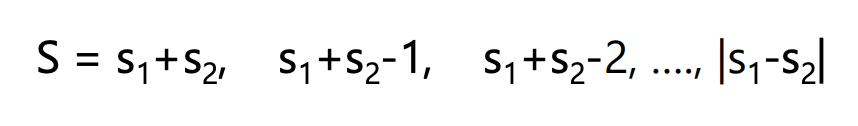
what is the ‘big J’ in the term

for a single electron:

J = j (j = l ± ½ )

for multiple electrons:

ALWAYS USE S NOT MULTIPLICITY

what do the resultant terms mean?

the terms represent possible substates

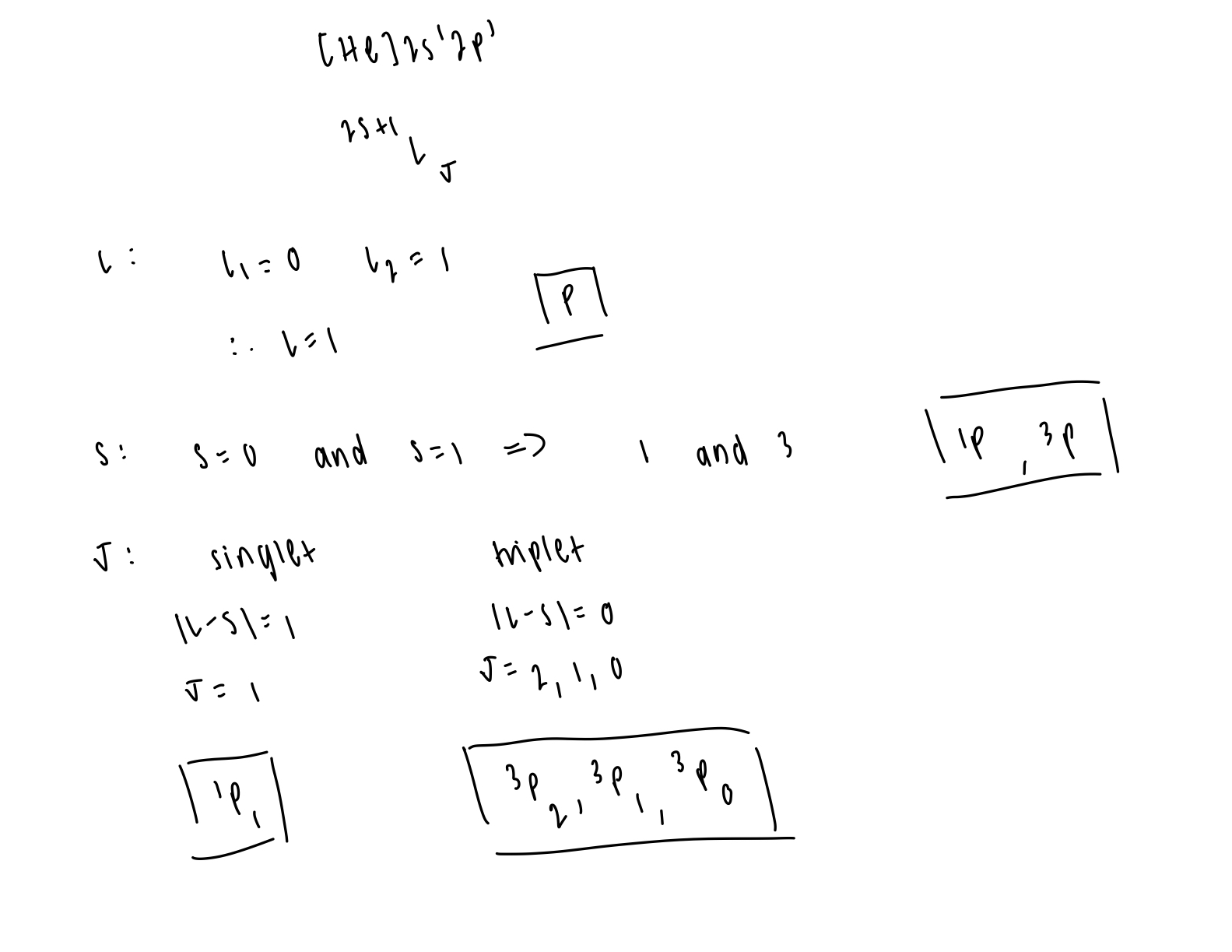
determine the possible terms and levels of [He]2s12p1

determine the possible terms and levels of partially filled shells of 2p13p1

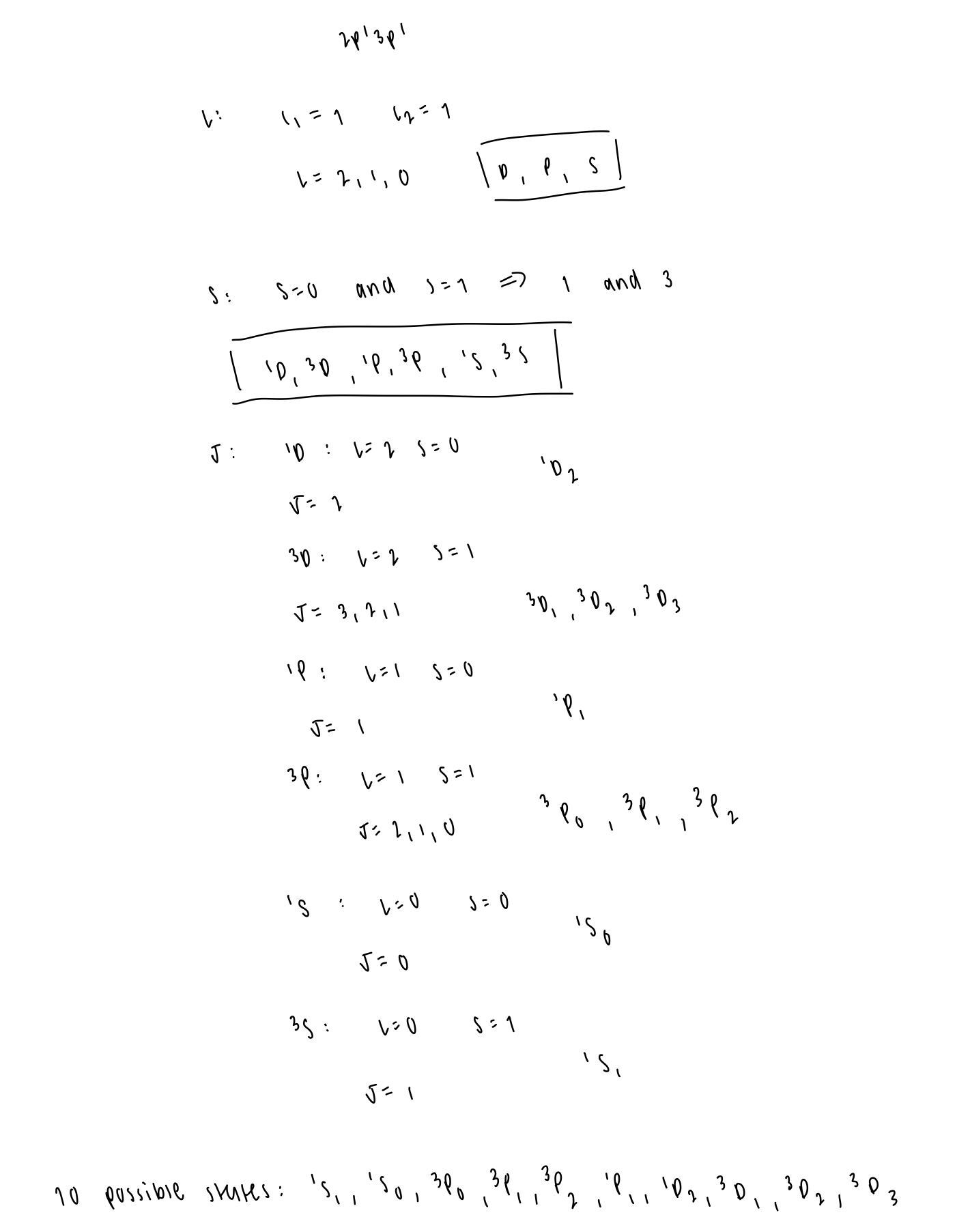
what is terms vs levels?

term = multiplicity and L value i.e. (3)P

level = multiplicity, L value AND J value i.e. (3)P(1)

describe holes

when there is a single gap in the configuration relative to closed shell, this can be treated as a single particle

Cl = 3p(5) ~ 3p(1)

determine the possible terms and levels of chlorine

what determines whether an electronic transition will occur?

• selection rules

• population of states

describe population of states and the probability of emission/absorption

emission = requires population of excited state

absorption = requires population of ground state

what gives rise to linewidth in atomic spectra?

• lifetime broadening

• Doppler broadening

• atomic collisions

describe lifetime broadening