Geometry: Notable Concepts & Proofs

Circle (Fact 1)

Shape formed by a set of points that are all the same distance away from a center point

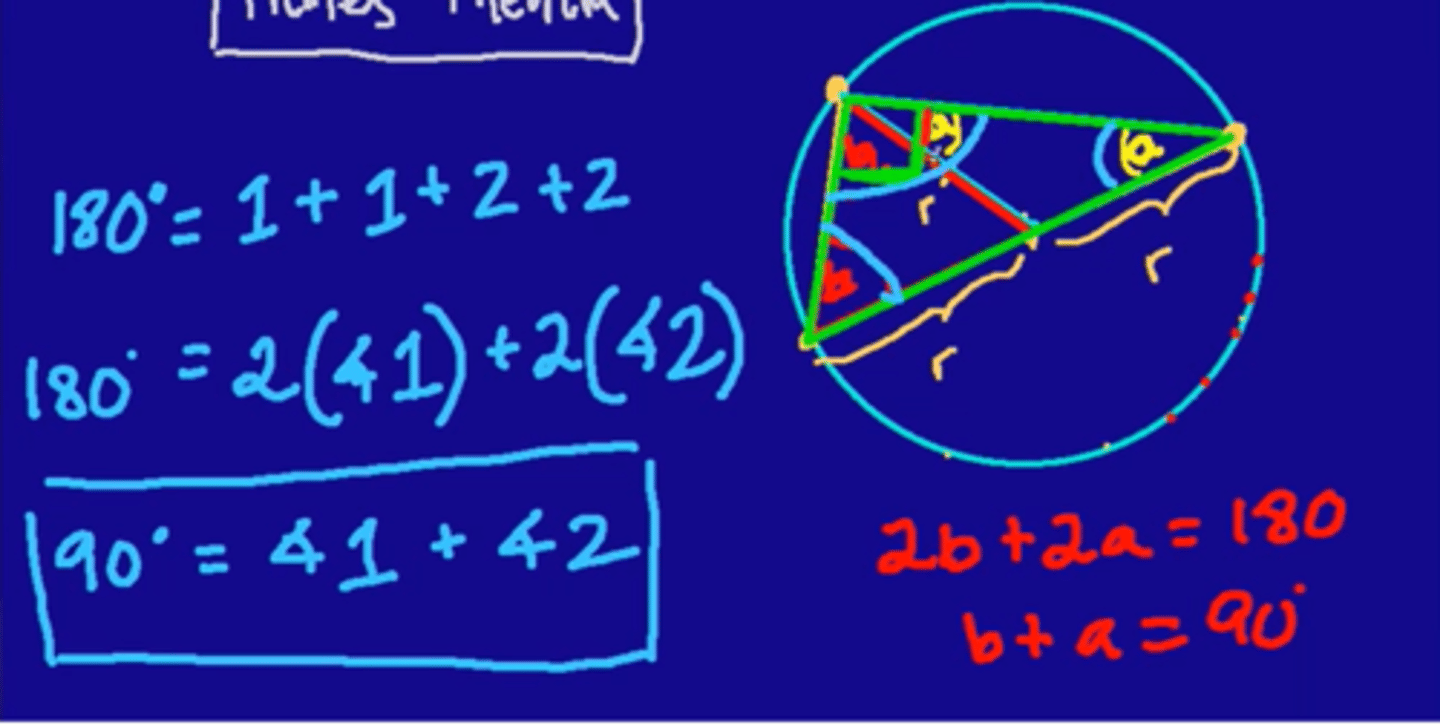
Thales' Theorem (Fact 1)

Theorem that states that Right triangles are always formed when connecting the dots out of any set of 3 points along a circle, 2 of which are the ends of a diameter line of the circle (for Proof, see Picture)

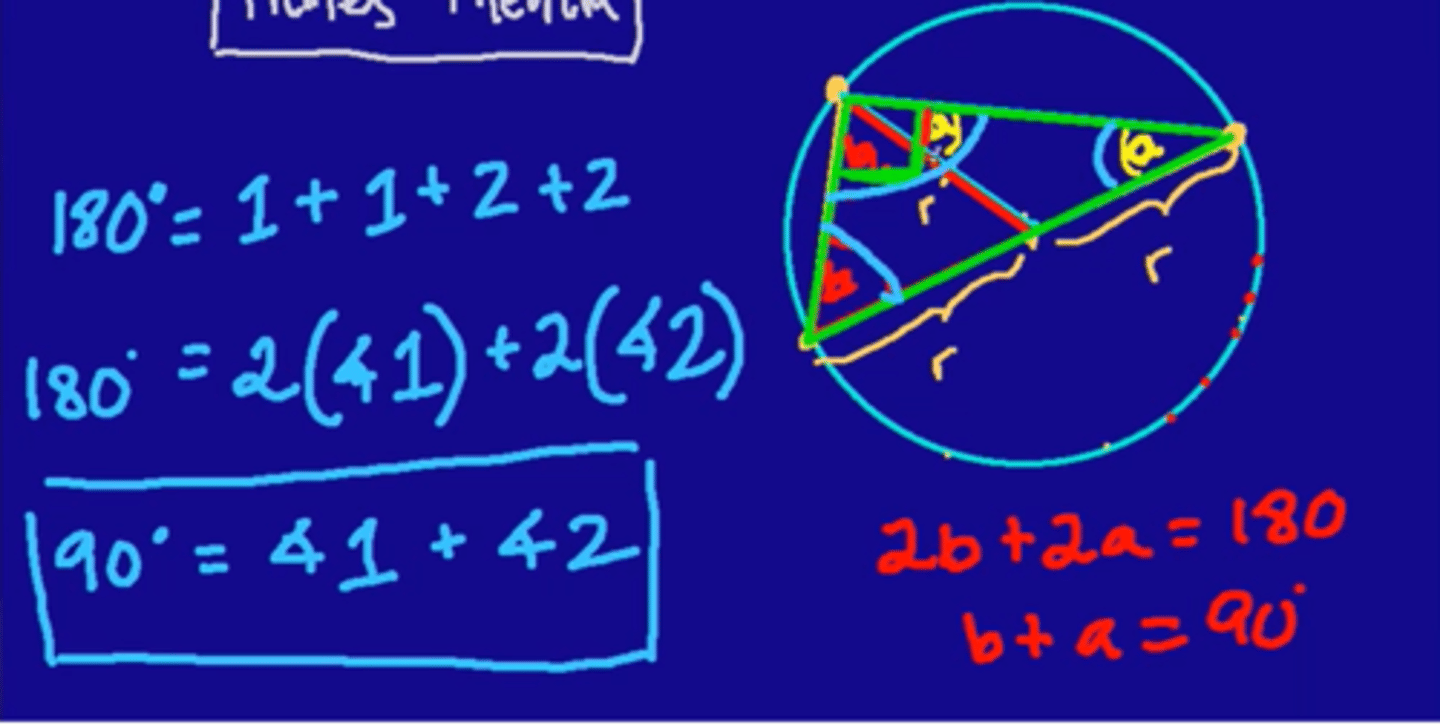
Thales' Theorem (Fact 2)

Theorem that states that the center of a circle (blue dot in picture) can be found by making 2 lines that run through the center of a circle and finding the point where they intersect each other which are made from first connecting 2 sets of diametrically opposed points which are made from first determining the points at which rays (of lines) come into contact with the circle which are made from first making 2 right angles anywhere on the circle (for Proof, see Picture)

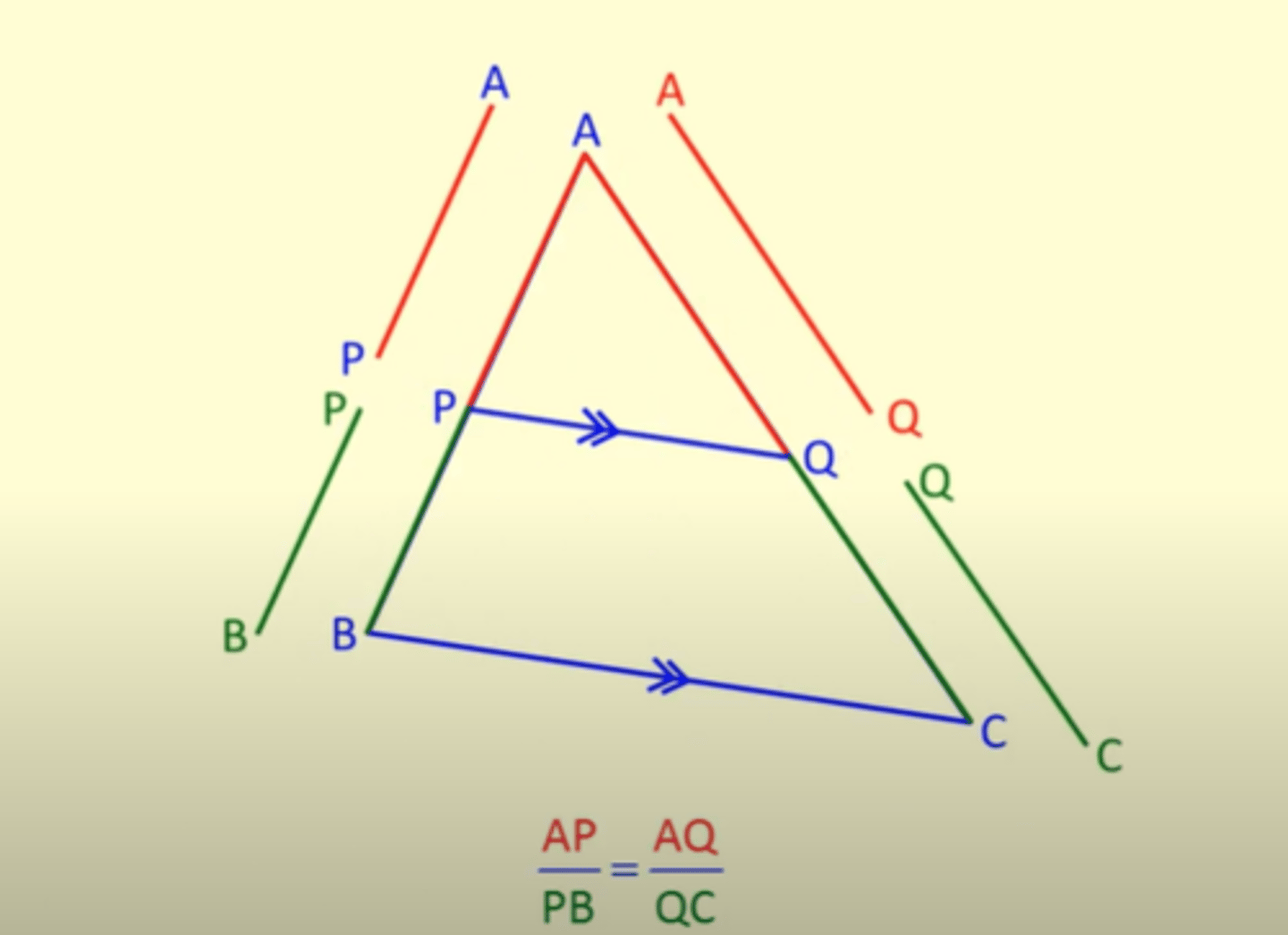
Proportional Intercept Theorem (Fact 1)

Theorem that states that if a line is drawn parallel to one side of a triangle through the triangle, then it divides the other two sides proportionally; likewise if two sides of a triangle are proportional to each other, then that means that the line running through the triangle making them proportional must be parallel

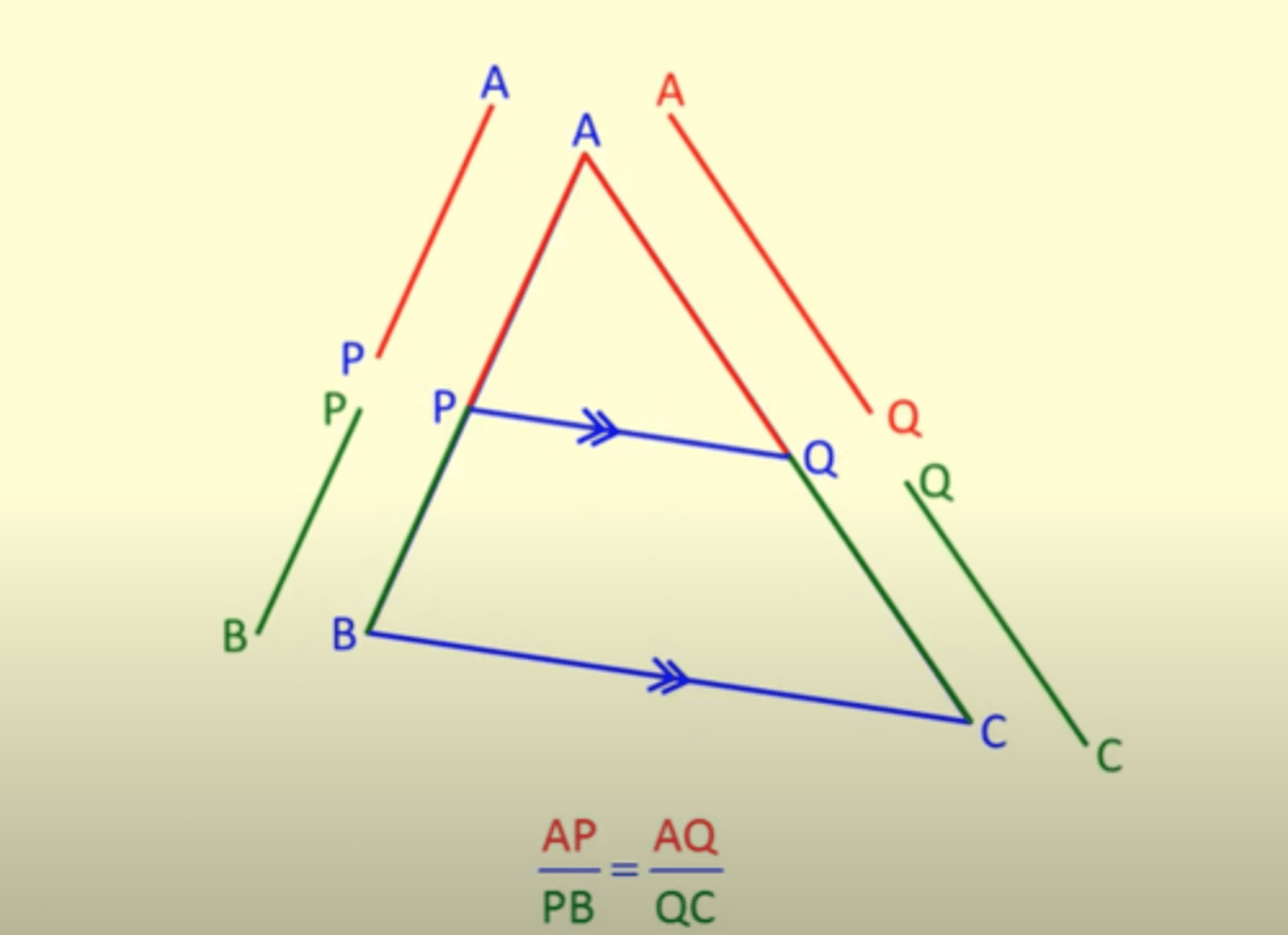
Proportional Intercept Theorem (Fact 2)

Theorem that states that if a transversal makes equal intercepts on three or more parallel lines, then any other line cutting them will also make equal intercepts

Thales' Theorem (Application 1)

Can be used to find the centers of circles

Isometry (Fact 1)

Type of Transformation that preserves distances that includes Translations and Rotations

Congruence (Fact 1)

Geometric Property of a shape relative to another shape which means the shapes can "fall together" or "fall into" each other, in other words it is a property exhibited by 2 or more shapes that have the same shape and size, composed of the exact same collection of points

Congruence (Fact 2)

Geometric Property of a shape relative to another shape which states the only reason it is not equal to another shape that is the same shape and size is because it is in a different position then the other shape and vice versa for the other shape

Congruence (Fact 3)

Geometric Property of a shape relative to another shape which occurs if every corresponding measurement of both comes out to be identical

Proportional Intercept Theorem Proof (Fact 1)

Lines, Segments, and Rays (All Concepts and Facts)

Lines go on forever

Rays have one point and the rest goes on forever

Line Segments have two points

For example, the universe can be represented by a line

For example, proportionalities can be represented by a ray

For example, an operation on the number line can be represented by a line segment

Parallel Lines are that never come in contact

Intersecting Lines always come in contact

Perpendicular Lines are Intersecting Lines with Right Angles always

When you have two Lines that are separate from each other and do not contact each other, remember they are lines and go on forever like parallel lines, so if you can draw a line from one intersecting normally or perpendicularly into one it is actually coming into contact and can be classified

When naming Lines that are Line Segments, name the letters in reverse alphabetical order but for all others keep it the same as written

Angles (All Concepts, Facts, and Fill-ins)

Angles are two rays whose points meet to form a certain figure

You may have heard that when you do a "360" you turn around in a circle once

With this, Geometrical measurements of angles actually use "degree" units kind of like temperature in science and weather

Acute Angles are those that are less than 90 degrees

Right Angles are those that are 90 degrees

Obtuse Angles are that are more than 90 degrees

Straight Angles are those that are 180 degrees

When naming Angles, start from the bottom down visually, not alphabetical, and make sure to put the appropriate angle sign as indicated electronically for notation

You can measure angles or such geometries with a protractor

A little curve drawing inside an angle indicates some sort of an Acute Angle

A bigger curve drawing inside an angle indicates some sort of an Obtuse Angle

A square drawing inside an angle indicates a Right Angle, which visually looks like ¼ of 360 degrees, meaning all Right Angles are always 90 degrees

Corresponding Angles are

Interior Angles are

Alternate Interior Angles are

Exterior Angles are

Alternate Exterior Angles are

Vertical Angles are

Adjacent Angles are

Supplementary Angles are

Congruent Angles are

Angle Sums of Polygons for a three sided polygon are

Angle Sums of Polygons for a four sided polygon are

Angle Sums of Polygons for a five sided polygon are

Angle Sums of Polygons for multiple sided polygons are determined by

Figures: Polygons and Prisms (All Concepts, Facts, and Fill-ins)

A figure is the general term for a concept of a 2D or 3D shape discussed in geometry

The first type of figure is of two dimensions and these figures are called Polygons

The second type of figure is of three dimensions and these figures are called prisms or 3D shapes aka Solids, which can be similar

Regular Polygons are 2D figures whose sides are the same length and whose interior Angles have the same degree

Irregular Polygons are 2D figures whose sides are not the same length, who may have different

Congruent Figures are those that

Similar Figures are those that

Zero Sided Polygons aren't polygons, but circles, with a bent line that wraps around to make the shape exist

Three Sided Polygons are called Triangles

Four Sided Polygons are called Quadrilaterals

Five Sided Polygons are called Pentagons

Six Sided Polygons are called Hexagons

Seven Sided Polygons are called Heptagons

Three Sided Polygons called Triangles can be acute meaning they have angles less than 90 degrees

Three Sided Polygons called Triangles can be obtuse meaning they have angles more than 90 degrees

Three Sided Polygons called Triangles can be right meaning they have one angle at 90 degrees, since if there were more it would turn into a quadrilateral such as a square

Three Sided Polygons called Triangles can be Equilateral meaning all of their sides are equal in measurement

Three Sided Polygons called Triangles can be Isosceles meaning two of their sides are equal in measurement

Three Sided Polygons called Triangles can be Scalene meaning none of their sides are equal in measurement

Four Sided Polygons called Quadrilaterals can be just Quadrilaterals meaning they have 4 sides, but they do not have parallel sides, right angles, or equal measures

Four Sided Polygons called Squares can be Parallelograms meaning they have parallel sides, but not right angles nor equal measures of the sides

Four Sided Polygons called Quadrilaterals can be Rhombuses meaning they have all four sides being congruent

Four Sided Polygons called Quadrilaterals can be Trapezoids meaning they have one pair of parallel sides

Four Sided Polygons called Quadrilaterals can be Rectangles meaning they have parallel sides and right angles, but not equal measures of the sides

Four Sided Polygons called Quadrilaterals can be Squares meaning they have parallel sides and right angles, and equal measures of the sides

All Squares can be Rectangles, but not all Rectangles can be Squares

All Rectangles can be Quadrilaterals, but not all Quadrilaterals can be Rectangles

All Rectangles can be Parallelograms, but not all Parallelograms can be Rectangles

Four Sided Polygons called Squares can be Kites/Diamonds meaning the are quadrilaterals with two pairs of sides that are congruent and adjacent, but not all 4

3D Figures are classified more conveniently by solid shape and number of faces

Zero Faced Solids are actually Spheres

One Faced Solids are actually 2D Figures such as Polygons since they represent a single, "flat" face

One Faced Solids with a sphere-like shape that ends in a point are called Cones

Two Faced Solids with a sphere-like shape between them are called Cylinders

Four Faced Solids of three triangles and one square are called Pyramids

Five Faced Solids

Six Faced Solids of all squares, or of 4 rectangles and 2 squares are called prisms

Rectangular Prisms are the names of these solids

Multiple Faced Solids are called multiple named based on the international geometric, mathematical, and scientific nomenclature standards

Congruence and Similarity (All Concepts, Facts, and Fill-ins)

2D Figures are congruent if they are the same shape, same size, same angle, same length, and same area

2D Figures are similar if they are the same shape, and have the same proportionalities as angles, length, and area

This means that Similar Figures have the same properties but are different sizes

This means the ratios of the lengths of their corresponding sides of the figures are equal

2D Figures are neither if they do not meet any of these expectations

2D Figures are congruent with each other if they maintain their congruence rules

2D Figures can also determine their congruence or similarity through them being able to be represented as two different figures on a graph which could go through a series of transformations such as translations, rotations, and reflections

Similar shapes mean corresponding angles are equal and the lines are in proportion

All Congruent Shapes are similar but not all Similar Shapes are Congruent