Topic 5 Flashcards: Calculus Concepts

Increasing/Decreasing Functions

Direction of Slope
As you may remember from studying linear functions, any increasing function [→] has a positive slope, and any decreasing function [↓] has a negative slope, and a flat/horizontal line [→] has slope = 0.

When we had linear functions, those were constant slopes, but the same theory applies to gradient functions, and due to this, we can have curves that switch between increasing and decreasing. What does the first derivative tell us about the slope of the graph?

When f'(x) > 0, the graph is increasing.
When f'(x) < 0, the graph is decreasing.
When f'(x) = 0, the graph is flat.

The purpose of finding f'(x) = 0

Checking where maximum and minimum is located

Is f(x)=e^2x an increasing or decreasing function, or both?

The function f(x)=e^{2x} is an increasing function because its derivative f'(x)=2e^{2x} is always positive for all x.

Find the derivative of y = 3x³ – 12x² + 8x + 1 using Power Rule

The derivative is y' =3(3)x-12(2)x+8(1) = 9x² - 24x + 8

Polynomial Derivatives

A polynomial derivative, also known as the differential coefficient or slope, is a concept that measures the rate at which the value of the function changes at any given point. The slope at any given point indicates how the function behaves locally and whether it is increasing or decreasing. The derivate also represents the slope of the tangent.

The first derivative of a function is the can be used to describe the velocity of an object.

Different rules of differentiation

include the power rule, product rule, quotient rule, and chain rule, which provide methods for finding derivatives of various functions.

Power Rule; Give an example

Example:
If f(x) = 4x⁷, then f'(x) = 4(7)x⁶ = 28x⁶

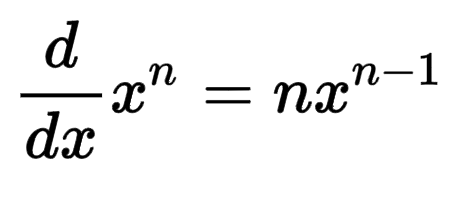
Product Rule; Give an example

Example:
If y= x²cos3x

then u = x² and v = cos(3x)

Then, using the product rule, y' = u'v + uv' = (2x)(cos(3x)) + (x²)(-3sin(3x)) = 2xcos(3x) - 3x²sin(3x)

This can be simplified to y’ = x(2cos(3x) - 3xsin(3x))

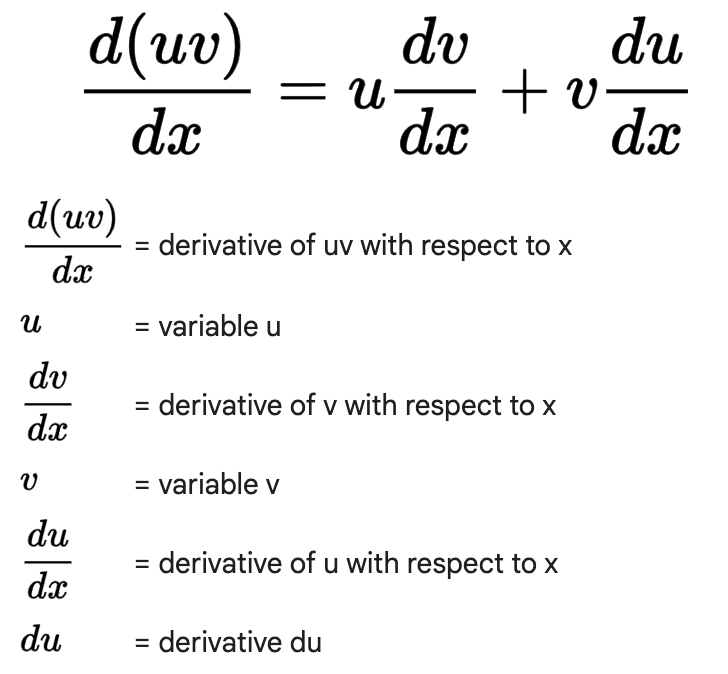
Differentiation f(x) = (1-x³)e^2x

u’ = -3ײ and v’=2e^2x

Using the product rule, differentiate to find f'(x) = u'v + uv' = (-3x²)(e^2x) + (1-x³)(2e^2x) = e^2x(2-3x² -2x³)

Differentiate y = x³(4-x)^1/2

u = x³ and v = (4-x)^1/2

u’ = 3x² and v’ = (-1)(1/2)(4-x)^-1/2

(note: v’ is obtained using Chain Rule)

y’ = uv’+vu’

y’ = x3(-1/2)(4-x)^-1/2 + (4-x)^1/2(3x²)

See remaining solutions for simplying this equation over a common denominator in image.

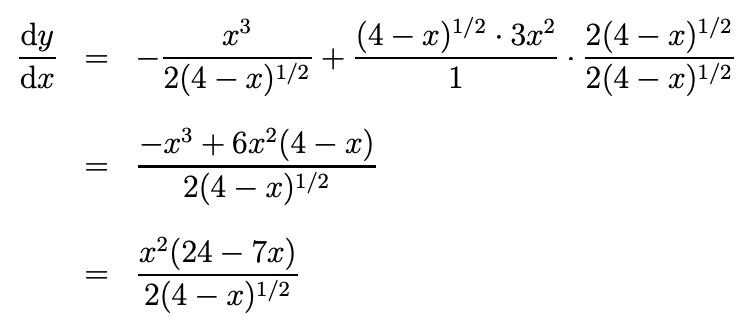
What is a tangent?

Equation of the slope at a given point (not just the slope itself).

• Can use point-slope formula to solve for equation of the tangent: y-y₁=m(x-x₁)

• Given f(x) and an x₁ value, you can do the following:

  1. Find y₁ using f(x₁)

  2. Find slope by differentiation; basically, find f’(x)

  3. Solve for m using f’(x₁)

     1. Substitute x₁, y₁, and m into y-y₁=m(x-x₁) and rearrange if needed.

What is a normal?

A straight line, passing through a given point, but perpendicular to the tangent. The gradient of the normal is negative reciprocal of the slope of the tangent, -1/m.

Integration

Anti-differentiation

The reverse of differentiating

Finding f(x) if given f’(x)

See imagine for notation, which reads “integral of f of x with respect to x”

Since the constant disappears when differentiating, when integrating, also replace the disappeared constant with +C. If a specific point is given, you can solve for the actual value of C. If working with definite integrals, you do not have +C.

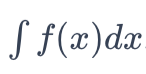
Second Derivative

f’’(x), y’’, or d²y/dx²

Tells us about the rate of change of the gradiant function

Second Derivate and Concavity

f is concave up on interval (a,b) if and only if f’’ is increasing on (a,b).

f is concave down on interval (a,b) if and only if f’’ is decreasing on (a,b).

When f’’ = 0, there is a possible point of inflexion

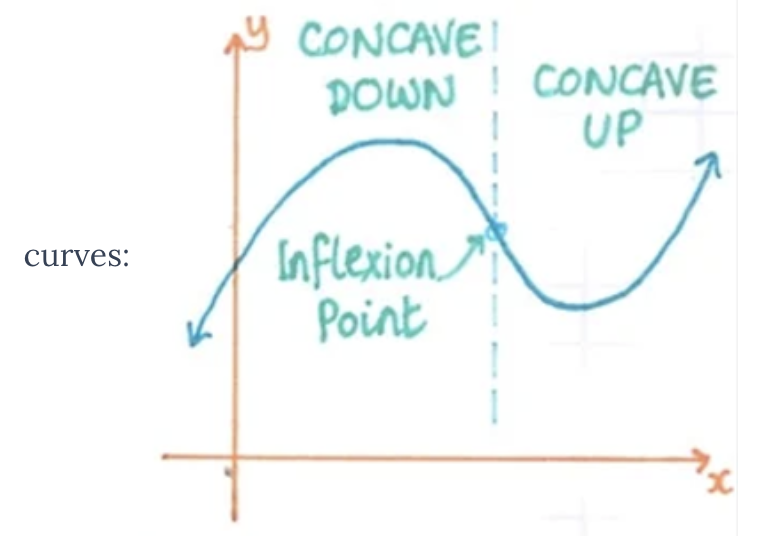
Point of Inflection

When f’’ = 0 (a root), there is a possible point of inflexion.

If f’’ changes from positive to negative (or vice versa) around the possible point of inflexion x, then x is a point of inflexion.

If the second derivative does not change in sign, then it’s not a point of inflexion.

Relationship between the graphs of f, f’, and f’’.

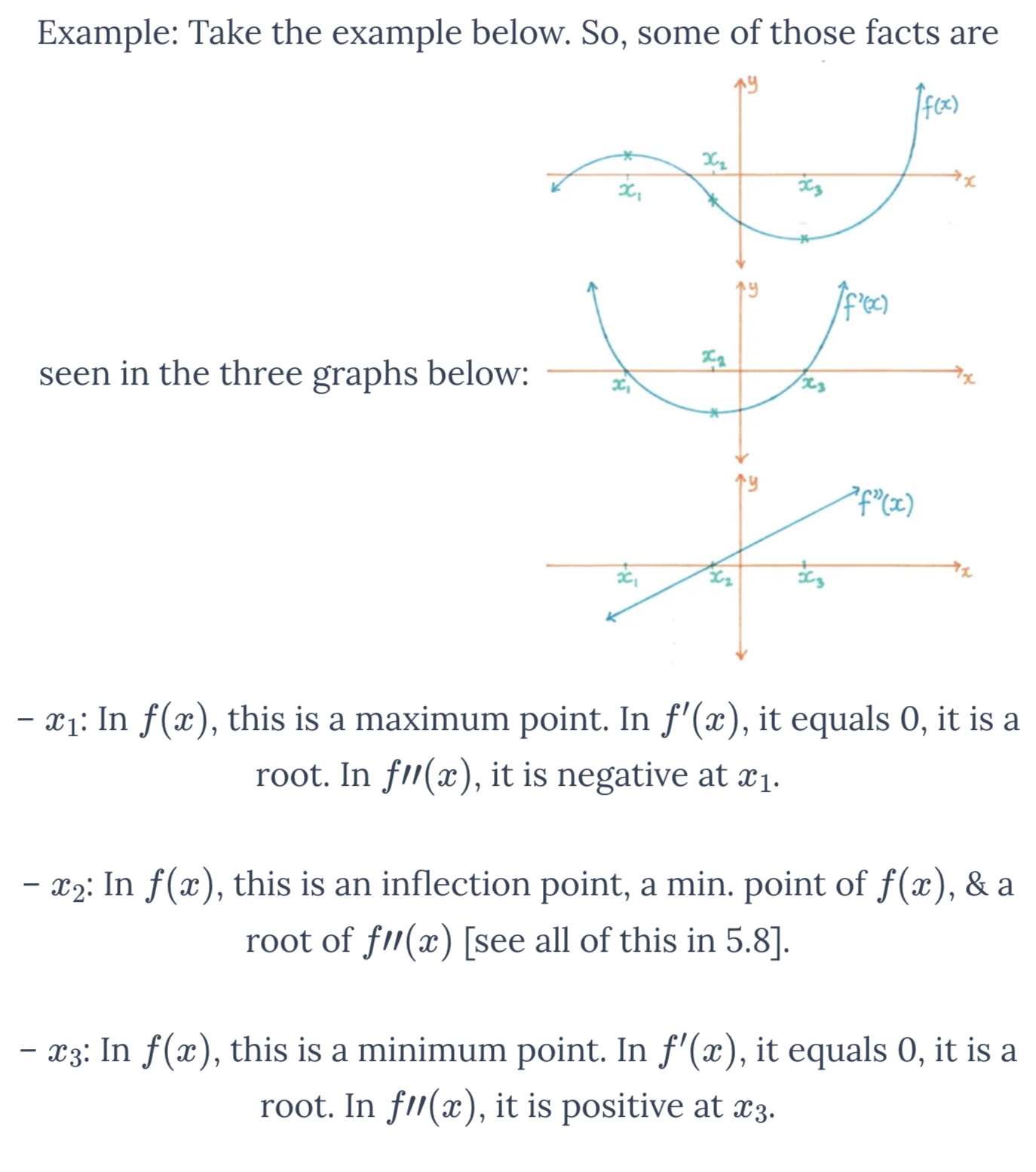
Max/Min Points of f(x)

Points where the first derivative f' changes sign, indicating local maxima or minima.

If we have a turning point (max or min) at x₁ and f’’(x₁)>0, then we have a minimum since the graph is concave up.

If we have a turning point (max or min) at x₂ and f’’(x₂)<0, then we have a maximum since the graph is concave up.

Optimisation

Using turning points (where gradient of f changes; where f’ changes sign) to optimise real-world functions, such as minimizing costs, maximizing areas, maximizing profits etc.

Minimization Problem:

a box has sides x, 2x, and 18-3x. Find the value of x where the volume of the box is the smallest.

Volume = x*2x*(18-3x) = 36x² - 6x³

To find the minimum volume, take the derivative of the volume function and set it to zero to find critical points, then determine which point gives the smallest volume.

dV/dx = 72x - 18x²= 0

18x(4-x)=0

hence x = 0 or 4.

since length can’t be 0, x=4.