Physics AQA A-Level Section 2 - Waves and Optics: Chapter 5: Optics

What can the wave theory of light be used to explain?

Reflection and refraction of light

What do light rays represent?

The direction of travel of wavefronts

What is the normal?

An imaginary line perpendicular to a boundary between two materials or a surface

What is refraction?

The change of direction that occurs when light passes at an angle across a boundary between two transparent substances

What happens between the refracted ray and the normal as it passes into or out of glass or air?

• Refracted ray bends towards the normal when it passes from air into glass

• Refracted ray bends away from the normal when it passes from glass into air

Does refraction take place if the incident ray is along the normal?

No refraction does not take place

What happens between the refracted ray and the normal as it passes a boundary between two transparent substances

• Bends towards the normal if it passes into a more dense substance

• Bends away from the normal as it passes into a less dense

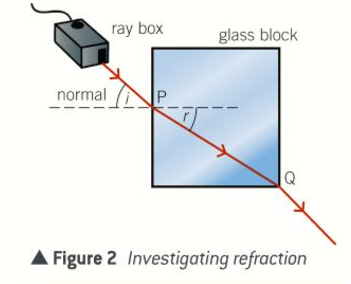
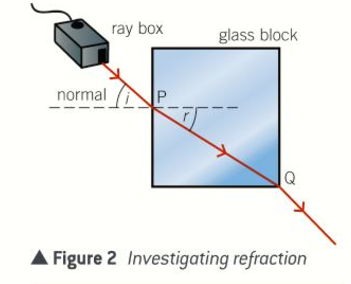
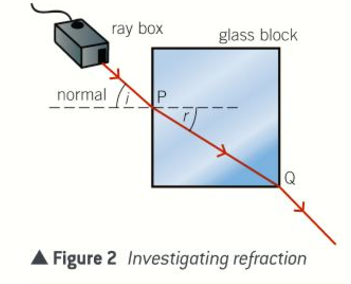
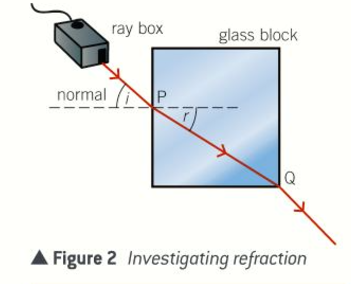
Describe how to investigate refraction of light by glass

• Use a ray box to direct a ray of light into a rectangular glass block at different angles of incidence at the midpoint P of one of the longer sides

• For each angle of incidence at P, mark the point Q where the light ray leaves the block

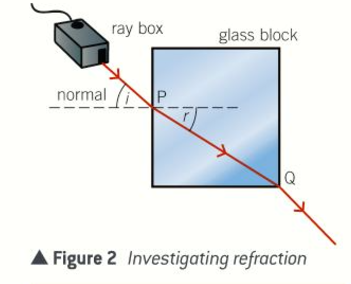
What do measurements of the angles of incidence and refraction for different incident rays show?

• The angle of refraction, r at P is always less than the angle of incidence, i

• The ratio of sin i/sin r is the same for each light ray.

• This is known as Snell’s law

• The ratio of sin i/sin r is the refractive index, n of the glass

Write the equation for the refractive index of a substance, n, for a light ray travelling from air into a transparent substance

The refractive index of a substance, n = sin i / sin r

When does partial reflection occur?

When a light ray in air enters glass (or any other refractive substance)

When is the angle of incidence the same as the angle of refraction for a light ray entering and exiting a glass block?

When the two sides of the block at which refraction occurs are parallel to each other

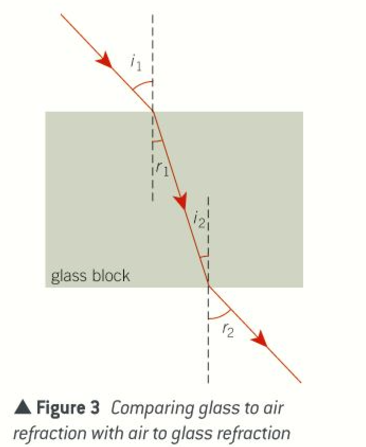
Explain the equation for the refractive index of glass

• If i₁ and r₁ are the angles of incidence and refraction at the point where the light ray enters the block

• Then the refractive index of glass, n = sin i / sin r

• At the point where the light ray leaves the block, i₂ = r₁ and r₂ = i₁

• Therefore, sin i₂/sin r₂ = 1/n

[Diagram of refraction of a monochromatic light ray by a triangular prism]

Why does refraction occur?

Because the speed of light waves is different in each substance

What does the amount of refraction depend on?

The speed of the waves in each substance (the bigger the difference, the more refraction there is going to be)

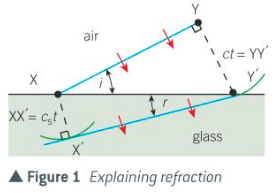
How To Derive The Equation for Refraction?

• Consider a wavefront of light when it passes across a straight boundary from a vacuum (or air) into a transparent substance

• Suppose the wavefront moves from XY to X’Y’ in time t, crossing the boundary between X and Y’

  In this time, the wavefront moves:

• A distance ct at speed c in a vacuum from Y to Y’

• A distance c_st at speed c_s in the substance from X to X’

  Considering Triangle XYY’, since YY’ is the direction of the wavefront in the vacuum and therefore perpendicular to XY, then YY’ = XY’, sin i, where i = Angle YXY’

• ct = XY’ sin i

  Considering Triangle XX’Y’, since XX’ is the direction of the wavefront in the substance and is therefore perpendicular to X’Y’, then XX’ = XY’ sin r, where r = angle XY’X’

• c_st = XY’ sin r

  Combining these two equations therefore gives:

• sin i / sin r = c / c_s

  Therefore, refractive index of substance is:

• n_s = c / c_s

How can you tell how high a substance’s refractive index is by observing the speed of light in said substance?

The smaller the speed of light is in a substance, the higher the refractive index of the substance

What’s another equation to get the refractive index of a substance?

n_s = λ/λ_s

How to derive equation for Snell’s law?

Consider a light ray crossing a boundary from a substance in which the speed of light is c₁ to a substance in which the speed of light is c₂ you get the equation:

• sin i / sin r = c₁ / c₂

• This equation may be rearranged as 1/c₁ sin i = 1/c₂ sin r

  Multiplying both sides of the equation by c, the speed of light in a vacuum gives:

• c/c₁ sin i = c/c₂ sin r

  Substituting n₁ for c/c₁ and n₂ for c/c₂ gives Snell’s law:

• n₁ sinθ₁ = n₂ sinθ₂ Where θ₁ = sin i and θ₂ = sin r

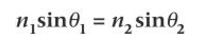
[Formula for refractive index]

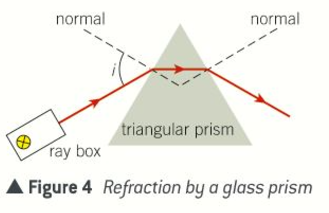
Why does white light split up into all colours of the spectrum when passing through a prism?

• White light composed of a continuous range of wavelengths: red at 650 nm to violet at 350 nm

• Glass refracts light by different amounts depending on wavelength

• Shorter wavelength in air = greater refraction so each colour refracted by a different amount

• Dispersive effect occurs because speed of light in glass depends on wavelength

• Violet light travels more slowly than red light so the refractive index of violet light is greater than red light.

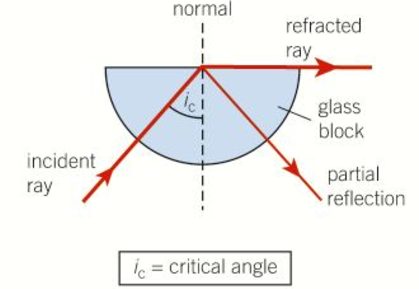
What happens to a light ray if its angle of incidence is equal to the critical angle?

The light ray refracts across the boundary of the material/medium

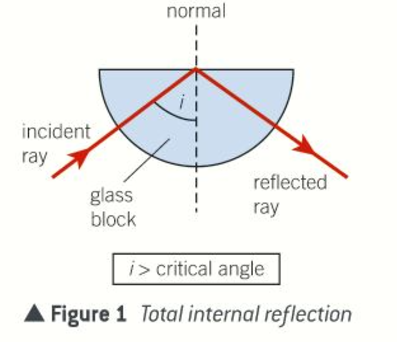
What happens to a light ray if its angle of incidence is greater than the critical angle?

It undergoes total internal reflection at the boundary, as if the boundary were replaced by a plane mirror

What happens to a light ray if its angle of incidence is less than the critical angle?

• Less dense —> More dense (Refracts towards normal)

• More dense —> Less dense (Refracts away from normal

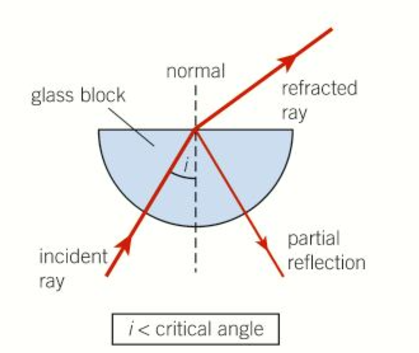
What are the two conditions needed for total internal reflection to take place?

• Incident substance has a larger refractive index than the other substance

• The angle of incidence exceeds the critical angle

Explain the equation for the critical angle

• At critical angle (i_c) the angle of refraction is 90° because the light ray emerges along the boundary

• Therefore, n₁ sin i_c = n₂ sin 90, where n₁ is the refractive index of the incident substance and n₂ is the refractive index of the other substance

• Since sin 90 = 1 then:

• Sin θ_c = n₂/n₁

Why do diamonds sparkle when white light is directed at them?

• When white light enters a diamond it is split into colours of the spectrum

• Diamond has a very high refractive index of 2.417 so it separates colour more than any other substance

• Diamond has a critical angle of 24.4°

• Therefore, a light ray in a diamond may undergo TIR many times before it emerges

• Its colours spread out more and more so the diamond sparkles with different colours

What are some uses for optical fibres?

• Medical endoscopes to see the inside of the body

• In communications to carry light signals

What happens as a light ray travels across an optical fibre?

• Light ray is totally internally reflected each time it reaches the fibre boundary, even where the fibre bends unless the radius of the bend is too small

• At each point where the light ray reaches the boundary, the angle of incidence exceeds the critical angle of the fibre

How does a communications optical fibre work?

Allows pulses of light that enter at one end, from a transmitter, to reach a receiver at the other end

How does the design of an optical fibre aid its function?

• Need to be highly transparent to minimise absorption of light, which would reduce the amplitude of pulses progressively the further they travel in the fibre

• Each fibre consists of a core surrounded by a layer of cladding of lower refractive index to reduce light loss from the core

• Light loss would reduce the amplitude of the light pulses

Where does TIR take place within an optical fibre?

Takes place at the core-cladding boundary at any point where two fibres are in direct contact

What would happen if there was no cladding in an optical fibre?

Light would cross from one fibre to the other if there was no cladding

What problems would the crossover of light between fibres cause?

The signals would not be secure as they would reach the wrong destination

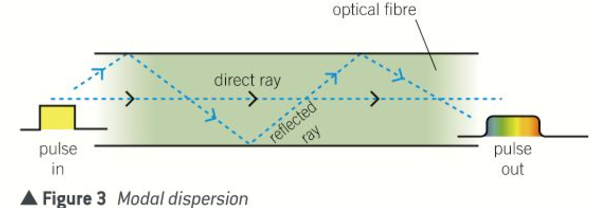
Why must the core of an optical fibre be very narrow?

To prevent modal dispersion

Why does modal dispersion occur in a wide core?

• Light travelling along the axis of a core travels a shorter distance per metre of fibre than light that repeatedly undergoes total internal reflection

• A pulse of light sent along a wide core would become longer than it ought to be

• If it was too long, it would merge with the next pulse