CPSY0900: Distributions & Z Scores

Distribution

How data is spread out over a range

What are the three types of common distributions?

Unimodal: one peak, most of the data clusters around one mode

bimodal: 2 peaks, indicates data comes from 2 different groups

uniform: all datapoints have the same frequency of occurrence 

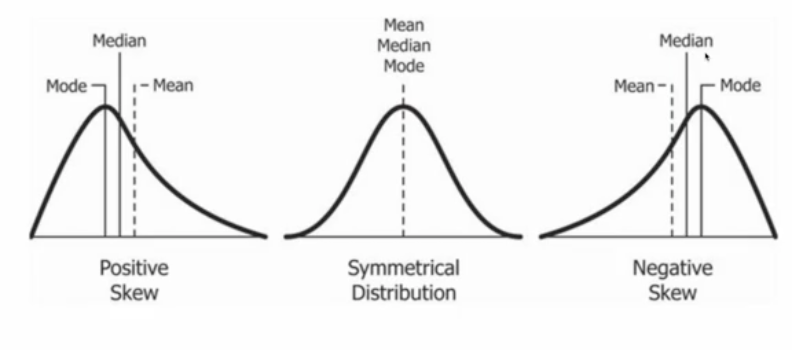
What are the three different types of skews?

Positive skew: tail to the left, mode < median > mean

symmetrical skew: no tail, mode = median = mean

negative skew: tail to the right, mean < median > mode 

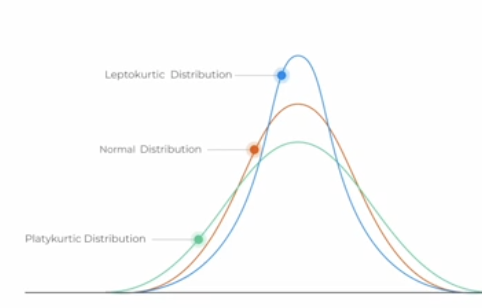
What is kurtosis? 

statistical measure that tells us whether a distribution is more or less peaked than the normal distribution 

<3: leptokurtic (more peaked) 

=3: mesokurtic (normal distribution) 

<3: platykurtic (less peaked) 

Why do researchers transform raw data?

When a distribution is skewed, statistical tests given invalid results because many statistical models rely on the assumption of distribution symmetry

What are the common data transformations?

What are the other names for a normal distribution?

Gaussian or bell shaped 

What are the unique properties of a normal distribution?

• no skew; data is symmetric around the mean

• mean = mode = median

• area under the normal curve = 1

• denser in the center around the mean, less dense at the tails

• defined by:

  • mean (determines the center)

  • standard deviation (determines the spread)

What is the 68-95-99.7 rule regarding the spread of a normal distribution’s data?

~68% of all data is within 1 SD from the mean

~95% of all data is within 2 SD from the mean

~99.7% of all data is within 3 SD from the mean

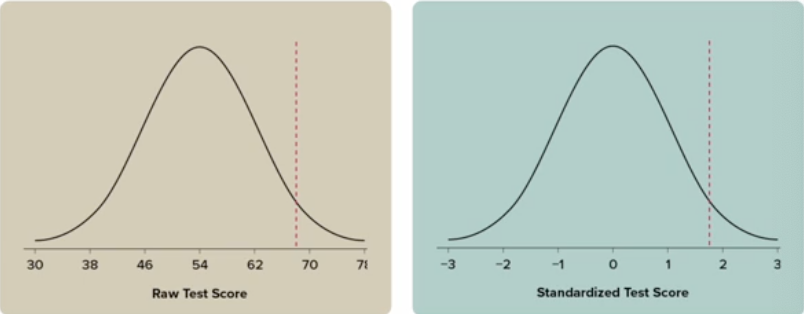
What is the standard normal distribution?

the mean = 0, and the SD = 1

it is used to compare data from different normal distributions by converting values into standardized z-scores

How to convert raw data to standardized data?

converting each data point into a z-score

• only the scale/values of the datapoints is adjusted; the trend of the curve looks the same

Z-score

number of SD a particular datapoint is from its mean

• converts raw to standardized metrics

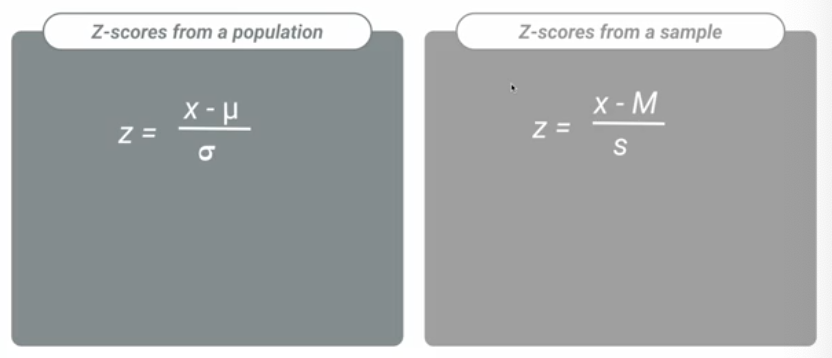
How do you calculate z-scores?

subtracting the mean from the value of interest, then dividing by the distributions SD

Interpreting z-scores: list the two variables you can consider and what each type of variable means about the given z-score

Sign

• positive z-score = the score is above the mean (right tail)

• negative z-score = the score is below the mean (left tail)

Magnitude

• how far away (in units of SD) the score is from the mean

Why is the magnitude of z-scores most often between -3 and 3? 

68-95-99.7 rule; most data falls between 3 SD of this range; z-scores outside of this range represent outliers 

Where would the following datapoints be on this graph based on their z-score?

• z-score of…

  • 1.5

  • -1.5

  • -0.5

  • 2.9

• 1.5 units above the mean (in between 1-2)

• 1.5 units below the mean (in between -1 and -2)

• between 0 and -1

• way out in the tail (near 3)

What if these values represented the age of dogs in a sample?

ex. 1.5 SD older than the average age of dogs in the sample

Converting raw scores to z-scores

1. calculate the mean

2. calculate the SS for variance and SD

3. calculate the z score: z = X - u(mean) / SD

• X = the value in the dataset whose z-score you’re trying to find 

What does the standard normal table do? 

provides cumulative probabilities associated with each z-score 

• tells what proportion of the data falls below that z-score 

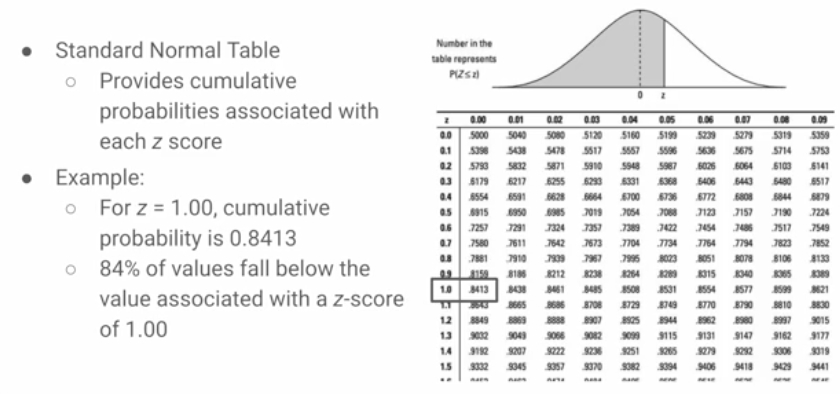
Understand this example regarding finding probabilities using Z-scores

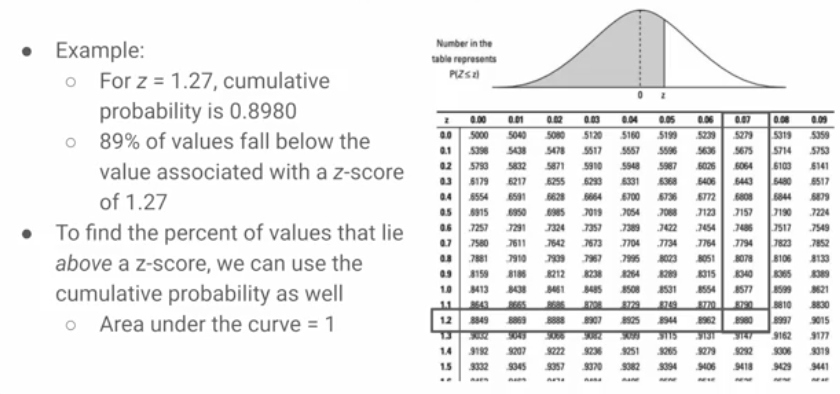
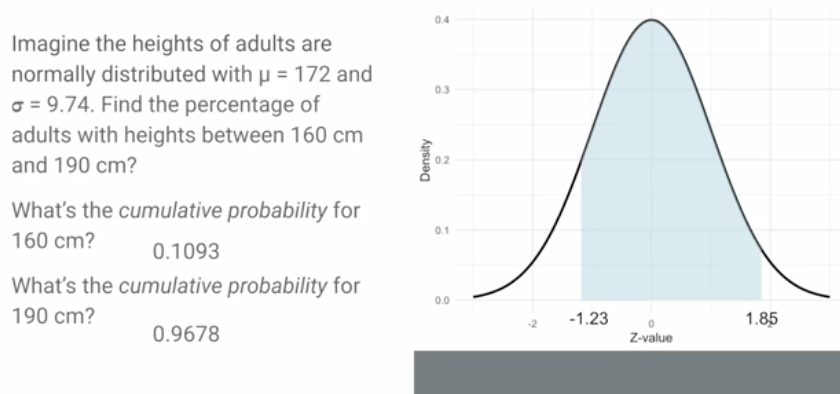
Finding the % of values that fall between 2 z-scores

subtract the cumulative prob of 160 cm from cumulative prob of 190 cm = % of the population with a height between 160-190 cm

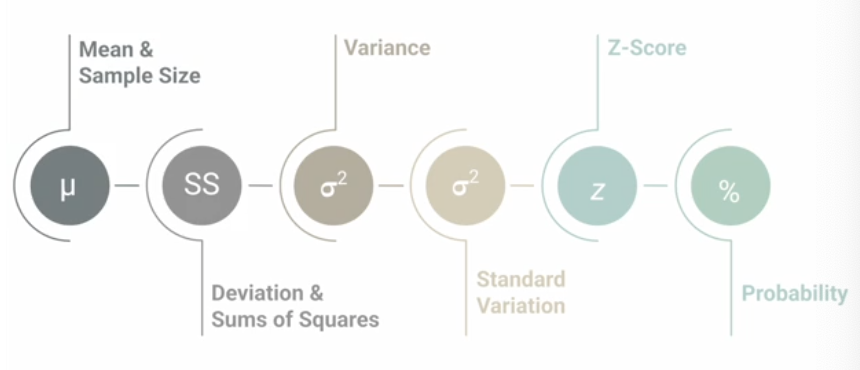
Step-by-Step approach to calculating Z-scores

1. mean and sample size of data (calculate deviations and sum of squares)

2. find variance and SD

3. calculate the z-score for the datapoint of interest

4. use the standard normal table (provided on canvas) to find the cumulative prob and interpret the area under the curve

• also helpful to sketch the distribution while doing these problems

  • mark the mean and z-score of interest

  • shade the area under the curve that represents the probability you’re calculating

    • gives you a clearer picture of how the data is distributed

Why are populations and samples different? 

• parameter vs. statistic 

  • parameter: numerical value that describes a population

  • statistic: numerical value that describes a sample

• sample is a portion of the population selected for a study

  • used to make inferences about the population being studied

• sampling methods can do their best to minimize bias

  • ensure the sample stats accurately reflect the population

Describe how the variance, SD, and z-score calculations differ for populations and samples

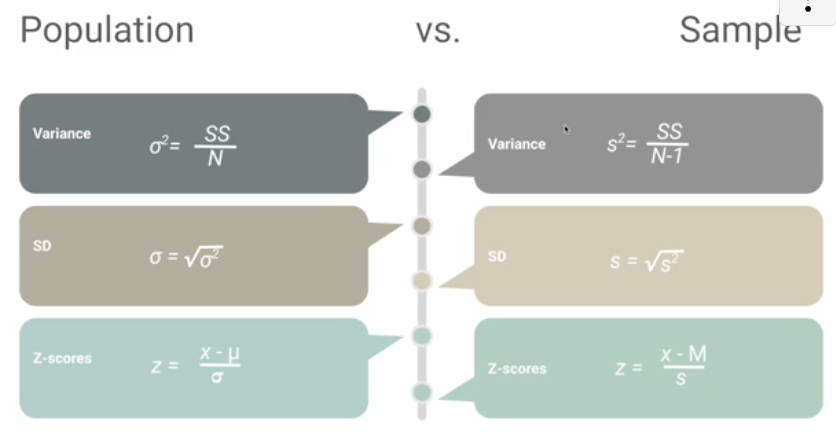
Why are degrees of freedom a factor when calculating sample values?

the N-1 adjustment compensates for the fact that samples tend to slightly underestimate the population variance

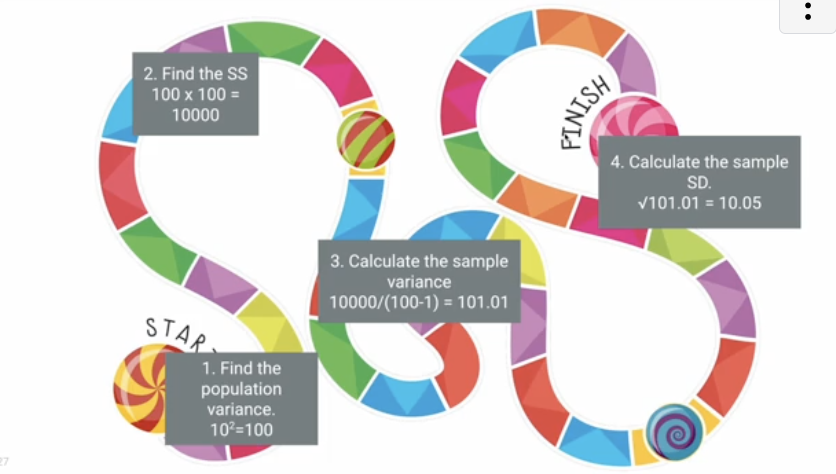
How do the SS for population and samples relate?

the SS is always the same for the sample and population

What is the effect of the N-1 adjustment when calculating variance for samples compared to that of populations? 

• the sample variance is always larger than the population variance due to the denominator adjustment (N-1)

• as sample size increases, the effect of subtracting (N-1) becomes smaller 

• larger sample sizes bring estimates of sample variance closer to that of the population variance 

  • aka: larger samples tend to reflect the population better