2 - Within and mixed design ANOVAs

What is a within-subjects design?

Also known as repeated measures design/ANOVA

A type of ANOVA where the same people have taken part in all possible levels of an IV

How is within-subjects different to between groups ANOVA?

It can control for individual differences, but risk a carryover effect (results could be due to order of conditions presented, fix through counterbalancing)

Different assumptions are made - we need to make an assumption of sphericity

Sources of systematic and unsystematic variability are different

Some degrees of freedom are slightly different

What is sphericity?

An assumption about variances

The difference between each pair of 'treatment levels' should have equal variance

variance_A-B = variance_A-C = variance_B-C

Only important if variable has three or more levels

If violated it increases the risk of Type 1 error

What happens when sphericity is violated?

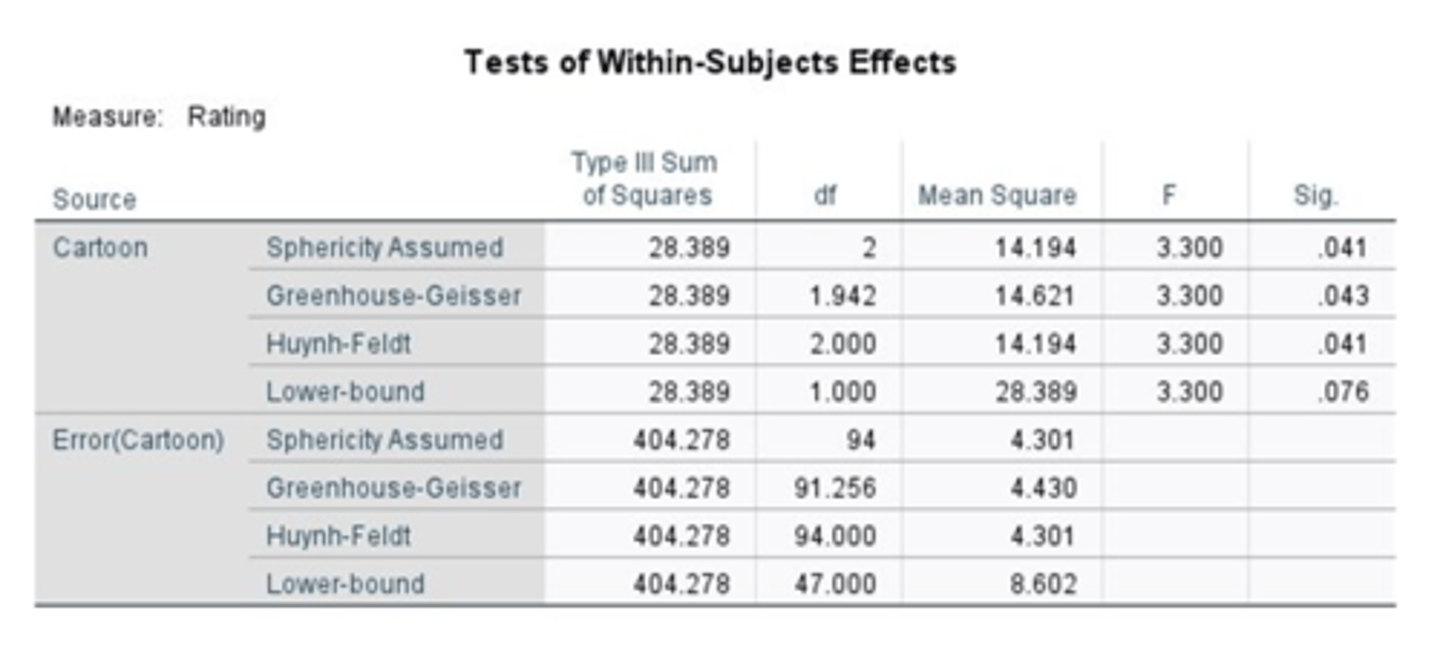
Must use Mauchly's test to assess whether variances of differences are equal

You want a p-value greater than .05 as that would mean there is no significant difference in the variability of those differences in condition levels across your repeated measures variables

If assumption is violated (i.e., p<.05) we (i.e., SPSS) make corrections to degrees of freedom

How to adjust degrees of freedom for sphericity?

If you don't need to correct sphericity you would just look at sphericity-assumed

Sphericity is corrected by multiplying original df by estimates of sphericity

This can have a knock-on effect for MS and F values

Generally okay to use Greenhouse-Geiser

How to calculate within-participant variability (SS_W)?

It exists as we've manipulated our independent variable within the person, not between people

We need to calculate individual sums of squares and add these up to get SS_W

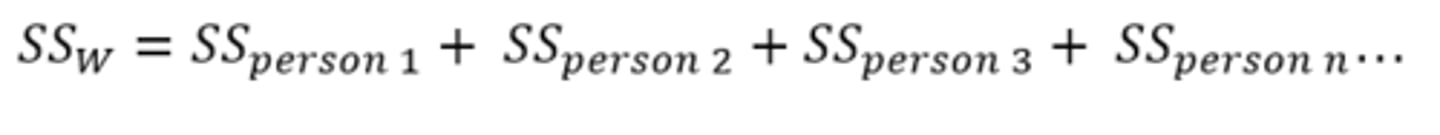
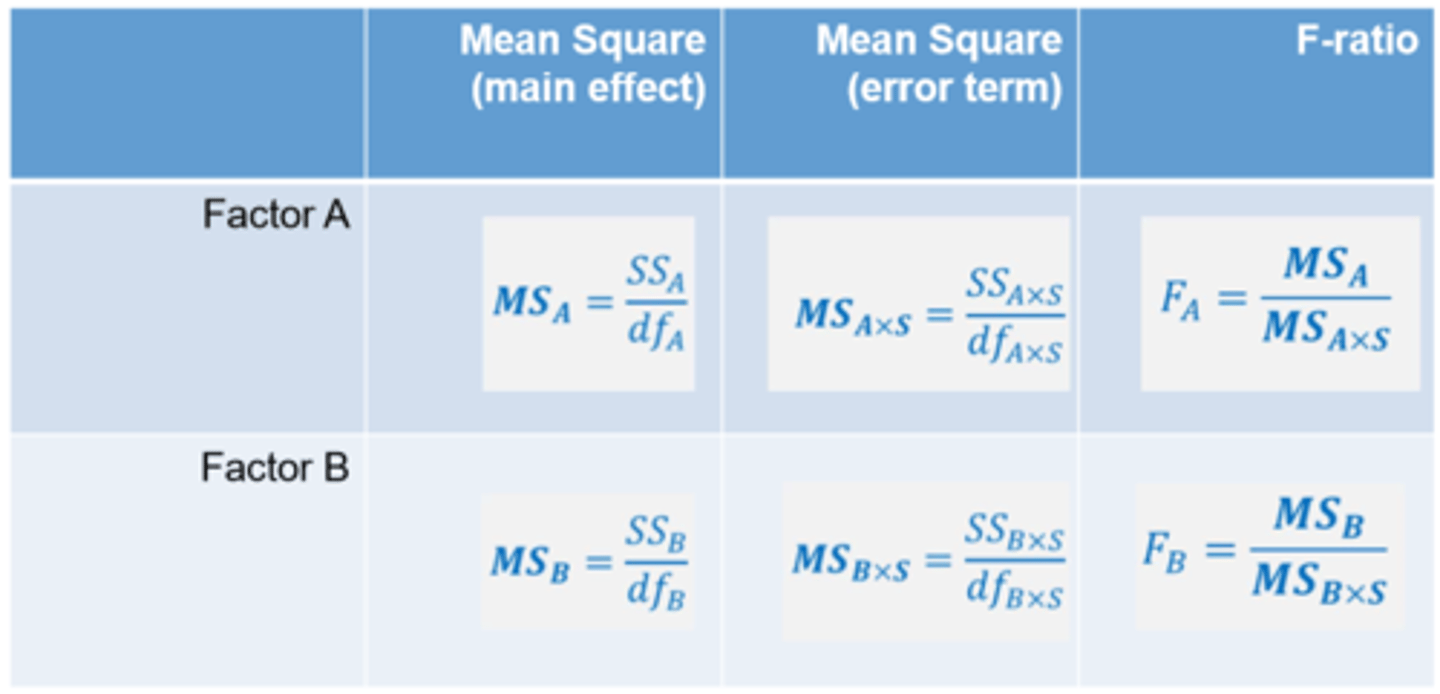
How to calculate two-way within-subjects ANOVA?

Need to break down the within-participant variability into different components

Partitioning variability for a two-way ANOVA requires different error terms for each main effect and interaction

Interaction =

Mean square (main effect) = SS_AXB / df_AXB

Mean square (error term) = SS_AXBXS / df_AXBXS

F-ratio = MS_AXB / MS AXBXS

How to calculate degrees of freedom for within-subjects ANOVA?

main effect df (SS_M)

= a-1 (number of levels of Factor A-1)

Error term df (SS_R)

=(a-1)(s-1) (main effect df x subject df)

What is a mixed-design ANOVA

An ANOVA that contains both between=groups and within-subjects independent variables

How do you partition variability in a mixed ANOVA?

Similar to between-groups and repeated measures ANOVAs

But the error term used in repeated measures and interaction effects is different

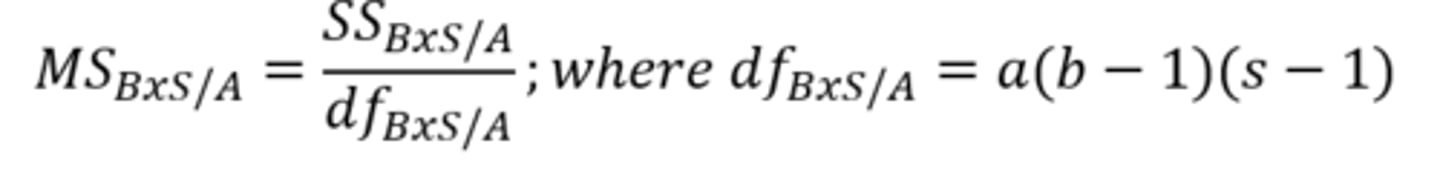
What are the mixed design ANOVA assumptions?

Need to meet the assumptions covered for both between and within subjects ANOVA

Need to check for:

Equality of error variance in between-groups factors - Levene's test

Equality of variances across different levels of within-subjects factors - Mauchly's test

Equality of covariance between within-subjects factors at each between-factor level - Box's M test