Distribuzioni di probabilità e intervalli (cap. 5 e 6)

Distribuzione binomiale

Distribuzione di probabilità che descrive il numero di successi in una serie di prove indipendenti, ognuna con due soli esiti possibili (successo/fallimento)

• fenomeno dicotomico: i risultati sono due e mutualmente escludentesi

• quando conosciamo la probabilità associata al verificarsi di un evento (p) conosciamo in automatico la probabilità che si verifichi l’altro evento (q) → 1 - p

👉 Esempio pratico:
Se lanci una moneta 10 volte, qual è la probabilità di avere esattamente 6 “testa”?

• n = 10, k = 6, p = 0,5

• P(X=6) = C(10,6) · 0,5⁶ · 0,5⁴

Variabili discrete vs continue

• Discreta: valori separati (interi).
  👉 Es.: numero di figli, lanci riusciti.
  👉 Distribuzioni: Binomiale, Poisson.

• Continua: infiniti valori in un intervallo.
  👉 Es.: altezza, peso, tempo.
  👉 Distribuzioni: Normale, t, χ², F.

Distribuzione simmetrica vs asimmetrica

• Simmetrica: la probabilità del successo è uguale a quella dell’insuccesso → la curva è “a specchio” rispetto alla media

• Asimmetrica: tanto più maggiore sarà la differenza fra probabilità successo/insuccesso → media, mediana e moda non coincidono

Distribuzione normale

Distribuzione di probabilità continua, a forma di campana, simmetrica rispetto alla media (Media = Mediana = Moda)

• intervalli (−∞ +∞)

• area sotto la curva = 1

Distribuzione normale standard

E’ una distribuzione normale “speciale”, ottenuta trasformando una normale generica in z-score

• Media (μ) = 0 (centrata sullo 0)

• Deviazione standard (σ) = 1

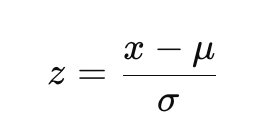
Teoria del Limite Centrale

La distribuzione delle medie campionarie tende ad essere normale, anche se la popolazione di partenza non è normale, purché la dimensione del campione sia sufficientemente grande (n ≥ 30 circa)

Legge dei grandi numeri

Man mano che il numero di osservazioni (n) aumenta, la variabilità campionaria diminuisce e se n tende all’infinito, l’errore standard della media campionaria tende a 0

Intervalli di fiducia

È un intervallo di valori calcolato da un campione che serve a stimare il parametro della popolazione (es. la media vera).

Es: un IC al 95% significa che, se ripetessimo moltissimi campioni, il 95% degli intervalli calcolati conterrebbe il vero valore del parametro

• IC 90% → z = ±1,645
  👉 Lascia il 5% di probabilità in ciascuna coda (totale 10%).

• IC 95% → z = ±1,96
  👉 Lascia il 2,5% in ciascuna coda (totale 5%).

• IC 99% → z = ±2,576
  👉 Lascia lo 0,5% in ciascuna coda (totale 1%).

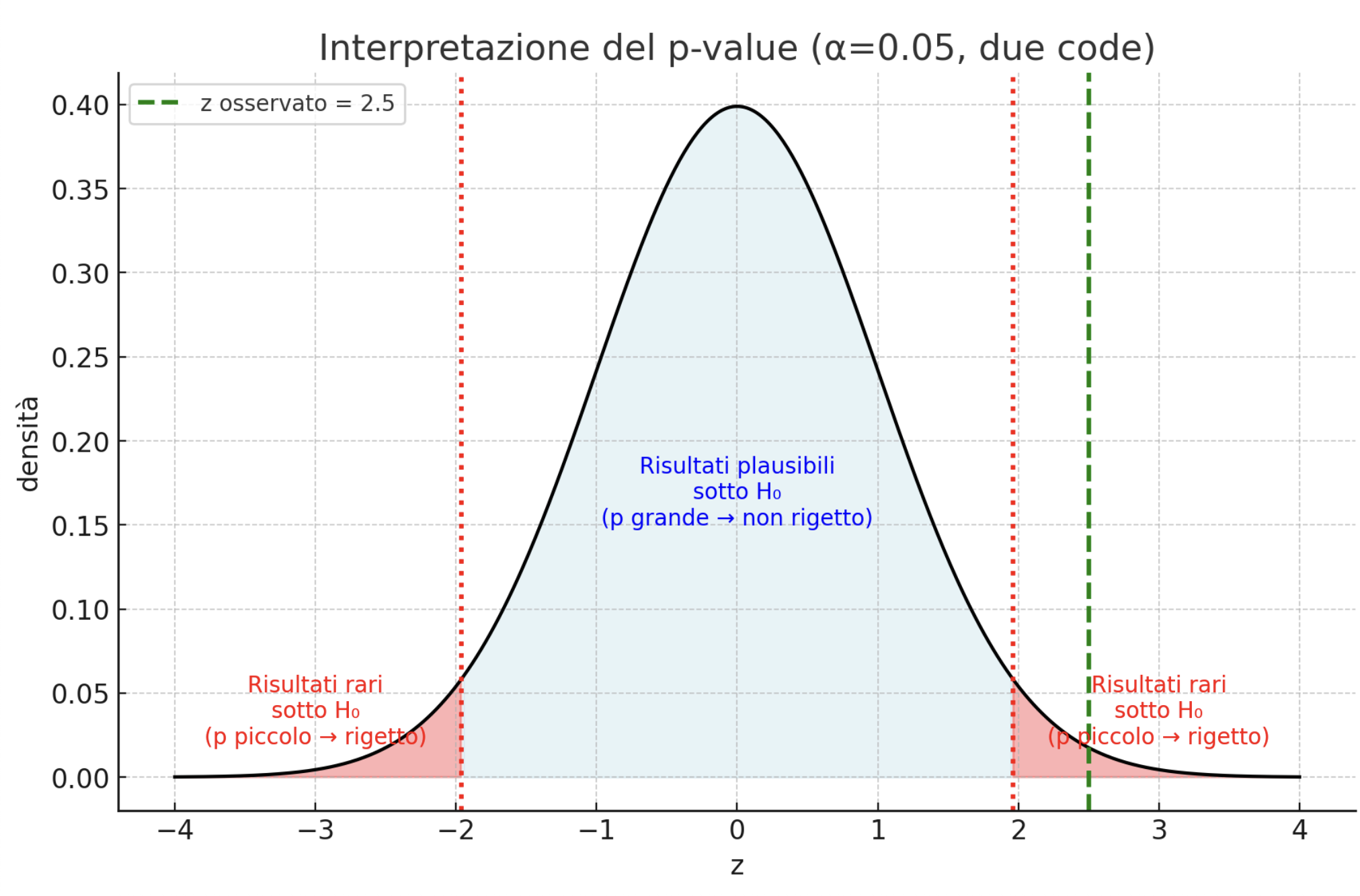
Che faccio se p-value ≤ α ?

❌ Rifiuto H₀ → la probabilità calcolata è inferiore al livello di significatività (= alfa)

• Risultato statisticamente significativo

• I dati suggeriscono che esiste un effetto/differenza

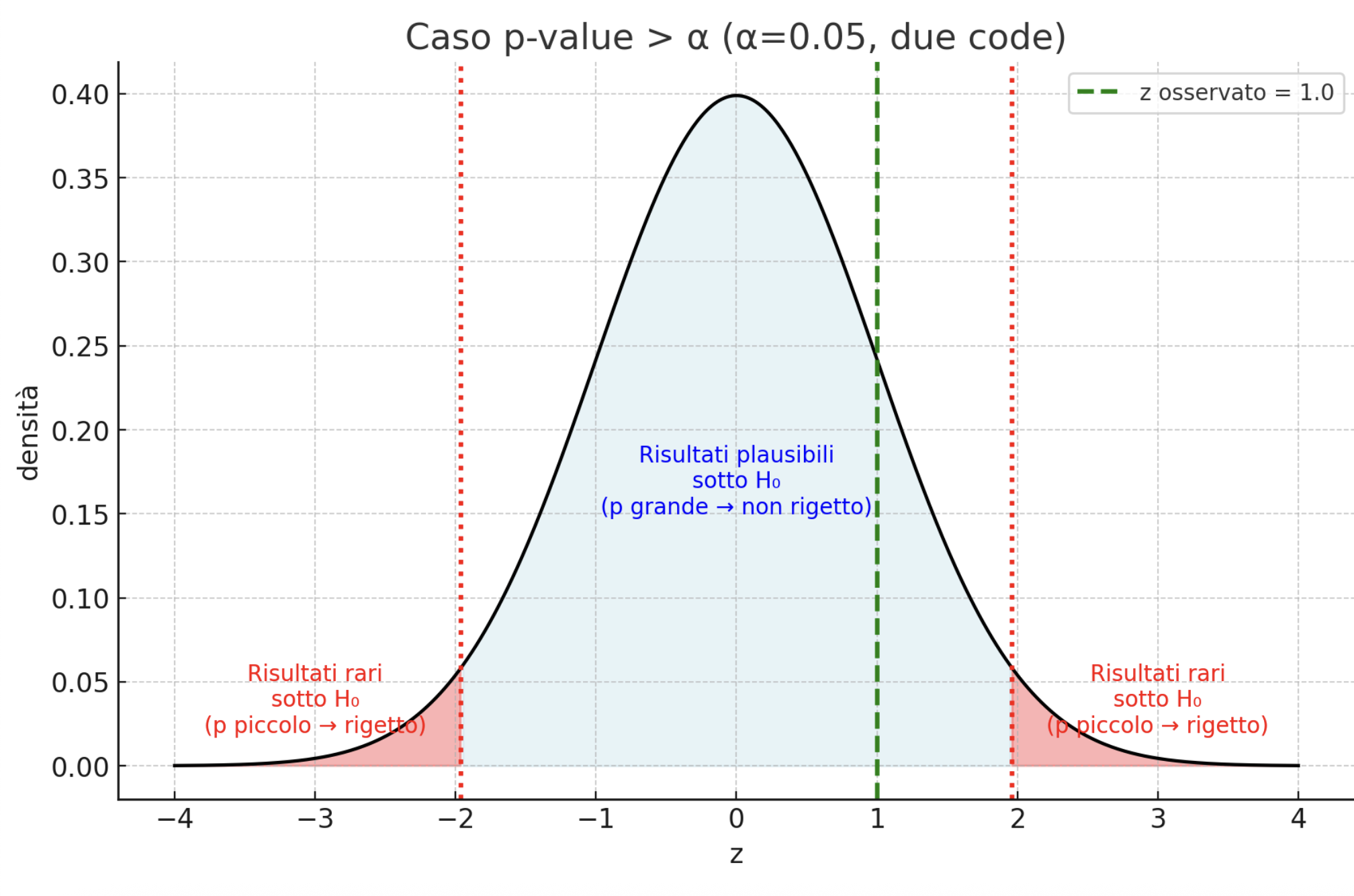
Che faccio se p-value > α ?

✅ non rifiuto H₀ → la probabilità calcolata è superiore al livello di significatività (= alfa)

• Il risultato è non significativo

• I dati non sono sufficienti per dire che c’è effetto/differenza

• 👉 Non vuol dire che H₀ è vera, ma solo che non abbiamo prove abbastanza forti per rifiutarla

Quali sono i tipi di ipotesi?

Ipotesi monodirezionale (a una coda)

• H₀: parametro = valore atteso

• H₁: parametro > valore atteso (test a destra)

• H₁: parametro < valore atteso (test a sinistra)

Ipotesi bidirezionale (a due code)

• H₀: parametro = valore atteso

• H₁: parametro ≠ valore atteso