Chapter 2: Principles of Special Relativity

What two developments questioned the Galilean principle?

• Newton’s view of absolute space, developed to explain inertial and rotational effects

• The discovery of EM waves, which seemed to suggest the existence of a universal medium

How did Lorentz consider the null experiment of the Michelson-Morley experiment?

He developed the mathematics to show that it was possible to explain the lack of a result if measurements of space and time were distorted by motion. However, he didn’t believe this was actually true.

How did Einstein approach the problem of the null result of the Michelson-Morley experiment?

He showed that the Galilean principle could only be made compatible with Maxwell’s equations if the speed of light was constant for all observers.

What is a light clock?

A light clock is a device that consists of two mirrors placed parallel to one another, with a beam of light bouncing between them. The light travels vertically between the mirrors, and each round trip of the beam is treated as a single “tick” if the clock. By timing how long each tick takes, we can see how time is flowing for different frames.

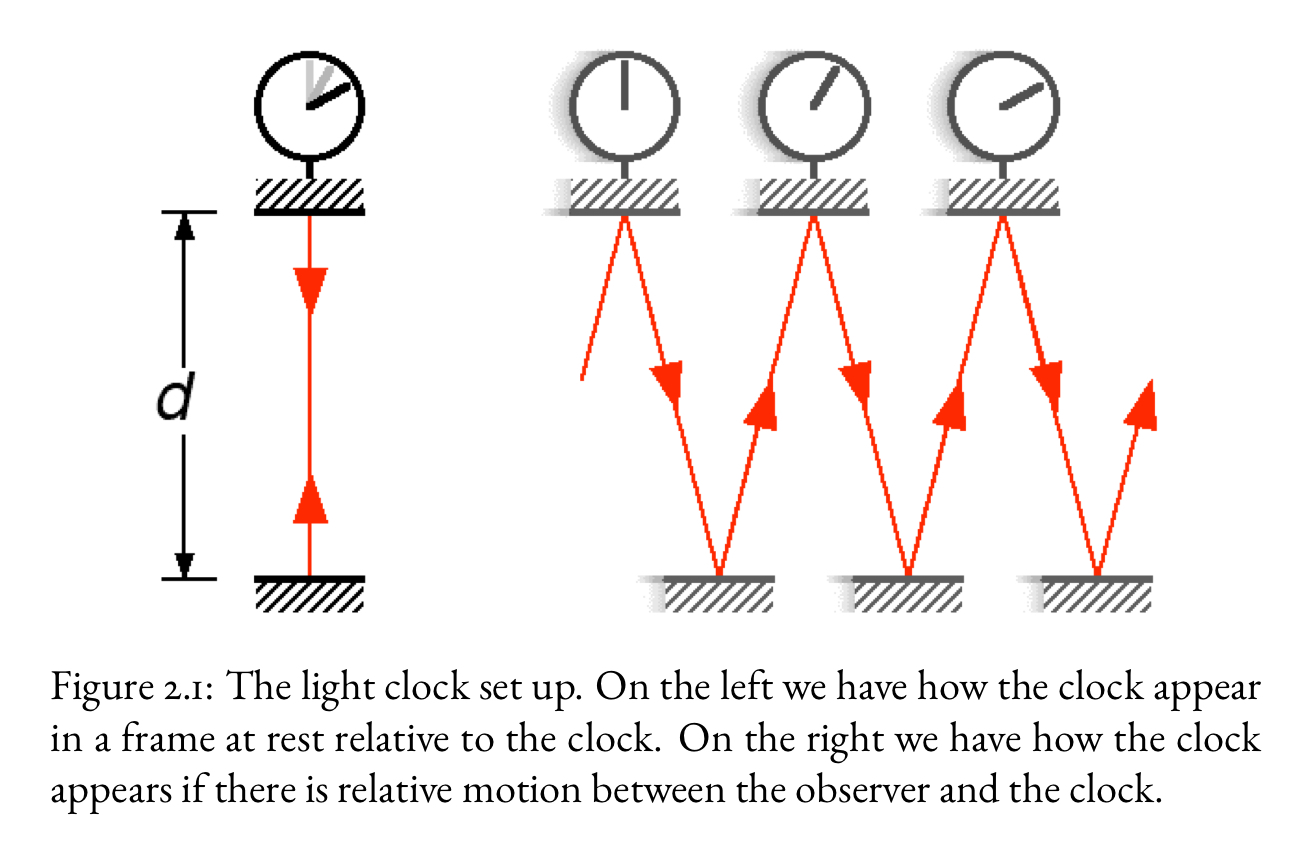
How can we analyse the behaviour of a light clock to investigate how space and time are related to the motion of light? - Show how a moving light clock shows time dilation.

The scenario is described from the perspective of S, the stationary frame, where S’, the rest frame of the clock, and the clock appear to be moving to the right with velocity v.

In S’, the light beam travels vertically between the mirrors. For one tick, the total distance travelled by the light is 2d where d is the distance between the mirrors. The time for one tick in S’ is given by \Delta t’=\Delta \tau = \frac{2d}{c} where \Delta \tau is referred to as the proper time, the time measured in the rest frame of the clock.

In S, the light follows a diagonal path due to the horizontal motion of the clock. During the time interval \Delta t observed in S, the clock moves a horizontal distance v \Delta t, while the light still travels between the mirrors. The light’s path forms the hypotenuse. The total distance travelled by the light in S is therefore 2 \sqrt{(\frac{v \Delta t}{2})²+d²} and the time for one tick is \Delta t = \frac{2 \sqrt{(\frac{v \Delta t}{2})²+d²}}{c} .

Rearranging and solving for \Delta t we get \Delta t = \frac{2d}{c \sqrt{1-\frac{v²}{c²}}}=\frac{\Delta \tau}{\sqrt{1-\frac{v²}{c²}}} . This result demonstrates the phenomenon of time dilation; since \Delta t < \Delta \tau, the moving clock ticks more slowly relative to the stationary observer in S.

How can the relationship between time intervals measured in two frames be expressed?

\Delta t = \gamma \Delta \tau, where \gamma is the Lorentz factor and \Delta \tau is the proper time

What is the value of the Lorentz factor?

\gamma=\frac{1}{\sqrt{1-\frac{v²}{c²}}} . To simplify notation further, we define \beta=\frac vc, giving \gamma=\frac{1}{\sqrt{1-\beta²}}

What is the Lorentz factor?

The Lorentz factor quantifies how relativistic effects such as time dilation and length contraction scale with velocity.

What is the effect of the Lorentz factor on time dilation and how is it affected by velocities close to the speed of light?

The size of the Lorentz factor determines how much time dilation has changed. The Lorentz factor remains extremely close to 1 even for velocities such as 0.5c. Only when velocities get very close to c does \gamma begin to become large. This means time dilation is a very small effect until velocities get close to the speed of light, at which point they can suddenly become extremely significant differences.

If c was \infty , \gamma = 1 —> pre-relativistic transformation where \Delta t =\Delta \tau therefore no time dilation.

How can we analyse the behaviour of a light clock to investigate how space and time are related to the motion of light? - Show how a rod of proper length L_p, with a light pulse bouncing between two mirrors at the rod’s ends, at rest in its own inertial frame S’ shows length contraction. Length is measured by the time taken to move a certain distance, between the start and end points of the object.

From the inertial frame S, the rod and its mirrors are seen to move at constant speed v to the right. Let L be the rod’s length as measured in S.

In S’, the light covers a round trip of 2L_p and completes one cycle in the time \Delta \tau = \frac{2L_p}{c}.

At t=0 in S, set the origin so that the rear mirror is at x=0 and the forward mirror at x=L. After a time interval \Delta t the rear mirror must move to x=v \Delta t and the forward mirror to x=L+v\Delta t . The light is emitted from the rear mirror at t=0 and travels at speed c to the right, until it meets the forward mirror at time t. The forward mirror has then moved from x=L to x=L+vt_1, while the light has reached x=ct_1 . Equating these positions gives t_1=\frac{L}{c-v}.

The relative speed on the return leg is c+v. The return time is therefore t_2=\frac{L}{c+v} . The total time of the light in S is therefore \Delta t= t_1+t_2=\frac{2Lc}{c²-v²}=2 \gamma² \frac{L}{c} .

By time dilation, a clock’s period measured in its rest frame must appear multiplied by \gamma in any frame where the clock moves at speed v. Hence, the round trip in S must be \Delta t = \gamma \Delta \tau = \gamma (\frac{2L_p}{c})

Equating these calculations gives L=\frac{L_p}{\gamma}, which shows that, as seen from S, the rod’s length is contracted by the factor \frac1\gamma relative to its proper length L_p. Since \gamma>1 for any nonzero velocity v, the length measured by the observer is always shorter than the proper length L_p. This phenomenon is known as length contraction.

In what direction does length contraction apply?

Only along the direction of motion so the dimensions of the object perpendicular to the motion are unaffected.

How was time dilation confirmed experimentally by measuring the decay of muons travelling at velocities v close to the speed of light c in the Earth’s atmosphere?

Muons are produced by collisions of atmospheric atoms with cosmic rays, which are high energy particles (mostly protons) originating from space. Setting v=0.9c , we can estimate the distance a muon travels in the Earth’s frame before it decays, provided that we know the mean lifetime of a muon in it’s rest frame. L will be the distance travelled before decay as measured in the Earth’s frame, and \Delta t_E Is the observed lifetime in the Earth’s frame. L_E=v \Delta t_E=\gamma v \Delta \tau

Lab experiments can be used to work out \Delta \tau , which is given as 2.2 \mu s . If we ignore relativity, L_E=2.2 \mu s * 0.9c = 594 m, which is significantly shorter than the typical height of muon production in the atmosphere (>1km). Thus, without time dilation, the majority of muons would decay before reaching the ground.

Since muons are detected on the Earth’s surface, this confirms time dilation effects are occurring, which means that \Delta t_E is much greater than the proper lifetime \Delta \tau, which allows muons to travel much farther than would otherwise be possible.

Derive the Lorentz transformation, which incorporates time dilation and length contraction and is therefore valid for all relative velocities, including those close to the speed of light.

Consider two inertial frames, S and S’ , with S’ moving at constant velocity v relative to S along the x-axis. At time t=0, the origins of the two frames coincide. Suppose an event P occurs at position x and time t in S, and at position x’ and time t’ in S’. We aim to find the relationship between (x,t) and (x’,t’).

The relation between x and x’ are governed by the relative motion which changes their relative distance measurements by vt and the relativistic contraction that happens in the x direction.

In the S frame, x=\frac{x’}{\gamma}+vt —> use t as the rate of time passing in S’ will not change how distance measurements will differ. In the S’ frame, x’=\frac xy-vt’

t’=\gamma (- \frac{vx}{c²}+t) and t=\gamma(\frac{vx’}{c²}+t’)

The forward Lorentz transformations between frames S and S’ in the x direction are written as:

c \Delta t’ = \gamma (c \Delta t - \frac{v \Delta x}{c})

\Delta x’ = \gamma (\Delta x - v \Delta t)

\Delta y’= \Delta y and \Delta z’=\Delta z

The only difference between the forward and inverse transformations is the sign of \beta, reflecting the relative motion of the two frames.

How did Lorentz transformations fundamentally alter the picture of classical mechanics?

Time and space are different in different frames, and when transforming between frames, the coordinates mix depending on the relative velocity between observers. Time is no longer universal, and spatial distances depend on the observer’s motion.

Why do we need a new notion such as spacetime?

Einstein’s second postulate, that the speed of light is constant for all observers, means that space and lengths cannot vary in some arbitrary way independent of how time is varying. Thus it explicitly constrains and interlinks space with time, such that we can only now talk about space time.

Derive the relativistic velocity formula using Lorentz transformations.

An object with velocity u’=\frac{\Delta x’}{\Delta t’} as measured in S’. Substituting the expressions for \Delta x’ and \Delta t’ into this definition, we have:

u’=\frac{\gamma (\Delta x - v \Delta t)}{\gamma (\Delta t - \frac{v}{c²} \Delta x)} = \frac{\frac{\Delta x}{ \Delta t}-v}{1-\frac{v}{c²} \frac{ \Delta x}{\Delta t}}=\frac{u-v}{1-u \frac{v}{c²}}

Where u=\frac{\Delta x}{\Delta t} is the velocity of the object in S and v is the velocity difference of the frames. The inverse relation, giving u in terms of u’, is:

u=\frac{u’+v}{1+u’ \frac{v}{c²}}

What is the non-relativistic limit and why are Galilean transformations still valid at low relative speeds?

At low relative speeds, the Lorentz transformations must reduce to the Galilean transformations. When v«c, \beta \rightarrow 0 and \gamma \rightarrow 1. In this limit, the Lorentz transformations become:c \Delta t’ = c \Delta t, \Delta x’ = \Delta x - v \Delta t Which are the Galilean transformations. Similarly, the relativistic velocity addition formula reduces to u=u’+v.