excel tings

What is nominal data?

• Definition: Data that represents categories or names with no order or ranking.

• Key Characteristics:

  • Used for labeling variables.

  • No mathematical meaning (you can’t sort, add, or subtract them).

  • Examples: gender (male, female), hair color (black, blonde, brown), country (USA, Japan, France).

What is ordinal data?

• Definition: Data that represents categories with a specific order, but the differences between ranks are not measurable.

• Key Characteristics:

  • Shows ranking or order.

  • You can say one is higher/lower, but not how much higher.

  • Examples: satisfaction rating (satisfied, neutral, dissatisfied), education level (high school, bachelor’s, master’s).

What is interval data?

• Definition: Numeric data with equal intervals between values, but no true zero point.

• Key Characteristics:

  • You can add and subtract values meaningfully.

  • No absolute zero, so ratios (like "twice as much") are not meaningful.

  • Examples: temperature in Celsius or Fahrenheit, dates on a calendar.

What is ratio data?

• Definition: Numeric data with equal intervals between values, with a true zero point.

What is central tendency? What are the 3 measures?

Central tendency refers to the idea of identifying the center or typical value in a set of data. It's a way to describe what is "normal" or "average" for a group of numbers.

Mean, Median, Mode.

What is the mean?

Mean (Average)

• Add up all the numbers and divide by how many numbers there are.

• Best used when data doesn’t have outliers.

• Example: (4 + 6 + 8) ÷ 3 = 6

• =AVERAGE

What is the median?

• The middle value when the numbers are ordered from smallest to largest.

• If there's an even number of values, it's the average of the two middle ones.

• Good for skewed data or when there are outliers.

• Example: In [3, 5, 9], the median is 5.

• =MEDIAN

What is the mode?

• The number that appears most frequently.

• There can be more than one mode, or no mode at all.

• Example: In [2, 4, 4, 6], the mode is 4.

• Mode works well for non-numeric data, not affected by outliers.

• =MODE

What is spread? What are the 4 measures?

Spread (also called dispersion) refers to how much the values in a dataset vary or how spread out they are around the centre (like the mean or median).

In simple terms, spread tells you how consistent or inconsistent the data is.

• Two datasets can have the same mean but very different spreads.

• Helps you understand variability, risk, or uncertainty in data.

Range, Standard deviation, Inter-quartile range, Variance

What is the range?

• The difference between the highest and lowest values.

• Example: If values are [3, 7, 10], the range is 10 − 3 = 7.

• Easy to calculate, but affected by outliers.

• =MIN, =MAX

What is inter-quartile range?

• The range of the middle 50% of the data.

• IQR = Q3 − Q1 (where Q1 = 25th percentile, Q3 = 75th percentile).

• More resistant to outliers than the regular range.

• =QUARTILE

What is variance?

• The difference between the values and the mean, square the difference, and then find the average of the squared values

• Gives an idea of how far numbers are from the mean, but in squared units.

• =VAR

What is standard deviation?

• The square root of variance.

• Measures average distance from the mean in the same units as the data.

• A small standard deviation means values are close to the mean; a large one means they're spread out.

• =STDEV

Explain Pearson’s product-moment correlation coefficient (parametric): r

Type: Parametric (assumes data is interval/ratio and normally distributed)

What it measures:

• The strength and direction of a linear relationship between two continuous variables.

Assumptions:

• Both variables are normally distributed

• Relationship is linear

• No significant outliers

• Data is interval or ratio scale

In excel: =PEARSON(array_1, array_2)

What the result tells you:

• r = 1 → Perfect positive linear correlation

• r = -1 → Perfect negative linear correlation

• r = 0 → No linear correlation

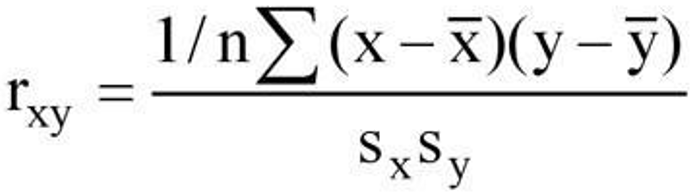
Explain Spearman’s rank correlation coefficient (non-parametric) rs

Type: Non-parametric (does not assume normality or linearity)

What It Measures:

• The strength and direction of a monotonic relationship (as one increases, the other tends to increase or decrease — not necessarily in a straight line).

Formula:

If no tied ranks: (view image)

Interpretation:

Same as Pearson’s r:

• rs= +1 perfect positive rank correlation

• rs= −1 perfect negative rank correlation

• rs= 0: No rank correlation

Assumptions:

• Ordinal, interval, or ratio data

• Relationship is monotonic (not necessarily linear)

• Can handle non-normal distributions and outliers

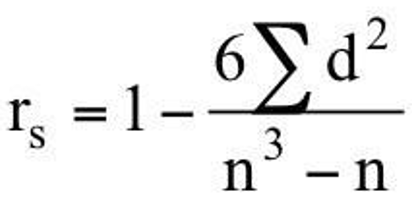
How do you calculate this in excel?

1. Enter your data

Let’s say you have:

• Variable X in cells A2:A10

• Variable Y in cells B2:B10

2. Rank the data

Use Excel’s =RANK.AVG()function to assign ranks:

• In column C, rank X values:

  =RANK.AVG(A2, A$2:A$10, 1)

• In column D, rank Y values:

  =RANK.AVG(B2, B$2:B$10, 1)
  

(The “1” means ascending order. Use “0” for descending.)

Fill both formulas down the column.

3. Calculate the Pearson correlation of the ranks

Now, use the =PEARSON() or =CORREL() function on the rank columns:

=PEARSON(C2:C10, D2:D10)

=PEARSON(C2:C10, D2:D10)

This gives you Spearman’s rank correlation coefficient (rs).

Interpretation of rs:

• rs = +1 → Perfect positive monotonic relationship

• rs = -1 → Perfect negative monotonic relationship

• rs ≈ 0 → No monotonic relationship

Notes:

• Spearman’s rs is used when data are ordinal or not normally distributed.

• It assesses monotonic relationships (not necessarily linear).

• If there are ties, RANK.AVG() handles them correctly by assigning average ranks.

Explain strength of correlation values

Explain regression analysis

Regression analysis is a statistical method used to understand the relationship between variables — especially how one variable (dependent) changes when another variable (independent) changes.

In simple terms: it’s about predicting one thing from another.

Key Components:

• Dependent Variable (Y): The outcome you're trying to predict (e.g., test score).

• Independent Variable (X): The factor you think influences or predicts Y (e.g., hours studied).

Simple Linear Regression (1 Predictor)

This is the most basic form of regression, with one independent variable:

Y= a+bX+ε

• Y = predicted value (dependent variable)

• a = intercept (where the line crosses the Y-axis)

• b = slope (how much Y changes for a 1-unit change in X)

• X = independent variable

• ε = error (difference between actual and predicted values)

Goal: Find the best line (regression line) that minimises the errors between predicted and actual values.

Multiple Regression (2+ Predictors)

Used when you have two or more independent variables:

Y = a+b₁X₁+b₂X₂+⋯+b_nX_n+ε

Each b_i shows the effect of X_i on Y, controlling for other variables.

Why Use Regression Analysis?

• Prediction: Forecast future outcomes (e.g., sales, grades, prices).

• Explanation: Understand how much one variable affects another.

• Control: Isolate the impact of one variable while holding others constant.

What are the assumptions of regression analysis?

Assumptions of Linear Regression (important to check):

1. Linearity: The relationship between X and Y is linear.

2. Independence: Observations are independent.

3. Homoscedasticity: Constant variance of errors.

4. Normality of errors: Errors (residuals) are normally distributed.

5. No multicollinearity (in multiple regression): Predictors aren’t too highly correlated.

How do you calculate regression in excel?

• Select Regression from the Data Analysis ToolPak: Data tab -> Data analysis group.

• If group does not appear as an option, install it as follows: File -> options -> add-ins -> in manage box select Excel add-ins -> click go -> check box by Analysis Tool Pak -> OK.

• Select the appropriate y and x variable ranges (remember that y is the variable that you want to Predict, i.e. the dependent variable).

• If your input data ranges include variable names, tick the Labels box and set the significance (i.e., confidence) level to 99%.

• Choose Output Range (to output the results on the same spreadsheet), and define your output range by entering a worksheet cell reference where you want to place the results.

• Tick the Residuals, Residual Plots and Line Fit boxes.

• Hit the OK button.

What are the key stats that are outputted?

Key Statistics in the Output:

1. Multiple R:

   • The correlation coefficient between the observed and predicted values.

   • A value close to 1 or -1 indicates a strong linear relationship.

2. R² (R-squared):

   • Represents the proportion of variance in the dependent variable (Y) explained by the independent variable(s) (X).

   • A value close to 1 means a good fit.

3. Adjusted R²:

   • Adjusts R² for the number of predictors, providing a more reliable measure for multiple predictors.

4. F-statistic and Significance F:

   • Tests the overall significance of the regression model.

   • A high F-statistic and a low Significance F (typically < 0.05) indicate a good model fit.

5. Coefficients (Intercept and X Variable):

   • Intercept: Predicted Y when X = 0.

   • X Variable: Slope, showing how much Y changes for a 1-unit change in X.

   • A p-value < 0.05 indicates the coefficient is statistically significant.

6. Standard Error:

   • Measures the precision of the coefficient estimates. Smaller values mean more accurate predictions.

Example:

• Multiple R = 0.95: There’s a strong positive linear relationship between X and Y.

• R² = 0.90: The model explains 90% of the variation in Y.

• Slope = 0.75: For each 1-unit increase in X, Y increases by 0.75.

• P-value for X = 0.002: The relationship between X and Y is statistically significant.

What are inferential statistics?

Assessing populations from samples.

What are the 5 steps of statistical tests?

1. A statement of the null hypothesis, and research hypothesis [which sets 1 or 2 tailed]

2. Set the level of risk – Statistical Significance (alpha value);

3. Select the appropriate statistical test [checking assumptions] and compute the test statistic value

4. Find Critical Value from published tables (or EXCEL)

5. Accept or reject the null hypothesis [to interpret data]

What are null and research hypotheses?

A hypothesis is a testable statement or prediction about a relationship between variables. In statistics, we use two types:

1. Null Hypothesis (H₀)

• Definition: The null hypothesis states that there is no effect, no difference, or no relationship between the variables.

• Purpose: It serves as the default or starting assumption in a statistical test.

• Example:
  “There is no correlation between hours studied and exam score.”
  (H₀: ρ = 0)

2. Research Hypothesis (H₁ or Ha)

• Definition: The research hypothesis (also called the alternative hypothesis) proposes that there is an effect, a difference, or a relationship.

• Purpose: It is what the researcher aims to support.

• Example:
  “There is a positive correlation between hours studied and exam score.”
  (H₁: ρ > 0)

How do you decide if your test is one or two tailed?

One-Tailed Test

• Use it when you are testing for a result in one specific direction (either increase or decrease).

• Example:
  “I think the new drug will increase recovery speed.”
  → You're only interested if it's better, not worse → one-tailed.

• Hypotheses:

  • H₀: μ ≤ μ₀

  • H₁: μ > μ₀
    (or the reverse if testing for a decrease)

Two-Tailed Test

• Use it when you're testing for any difference, regardless of direction.

• Example:
  “I think the new drug will have a different effect (could be better or worse).”
  → You're checking for any change → two-tailed.

• Hypotheses:

  • H₀: μ = μ₀

  • H₁: μ ≠ μ₀

Simple Rule of Thumb:

• Ask: “Do I care which direction the effect goes?”

  • Yes → One-tailed

  • No, any change matters → Two-tailed

Explain correlation coefficient

The correlation coefficient is a statistical measure that describes the strength and direction of a relationship between two variables.

Key Points:

• Symbol: Usually denoted by r (for Pearson correlation coefficient).

• Range: Always between -1 and +1.

  • r = +1: Perfect positive correlation — as one variable increases, the other increases in a perfectly linear way.

  • r = -1: Perfect negative correlation — as one variable increases, the other decreases in a perfectly linear way.

  • r = 0: No linear correlation — there's no predictable relationship between the variables.