AP Physics C: Mechanics Equations Ultimate Guide
1/51
There's no tags or description
Looks like no tags are added yet.
Name | Mastery | Learn | Test | Matching | Spaced | Call with Kai |
|---|
No study sessions yet.
52 Terms
W= change in Ek
Work-energy Theorem states that the work done by the applied force is equal to the change in kinetic energy. .
W=Fd
Work is equal to the area under the curve of a force x displacement graph, so if is a non-constant force, you integrate the force function.
Work by Gravity
Gravity does positive work on a falling object because the force of gravity is acting in the same direction as the displacement of the object. This causes the object to gain kinetic energy as it falls.
Similarly, gravity does negative work on an object moving upwards.
KE1 + U1 + W nonconservative = KE2 + U2
Work-energy theorem taking account of non conservative forces (always valid and always applicable).
Parallel Axis Theorem
This theorem states that the moment of inertia of an object about any axis is equal to the moment of inertia about an axis through the center of mass plus a product of mass and distance squared.
Ip = Icm + Md²
d is the location from the center of mass.
Icm is the moment of inertia for that particular shape.
Ip is the moment of inertia of the object while passing through point P.
F(x)= - dU/dx
This is the relationship b/w potential energy and force in a conservative force field (no non-conservative forces).
word
yes
Conservative Force
This exists when the work done by that force on an object is independent of the object's path. Instead, the work done by a conservative force depends only on the end points of the motion. An example of a conservative force is gravity.
Non-Conservative Force
These forces are forces that depend on the path taken, and they dissipate mechanical energy into other forms. Examples of BLANK forces include friction, air resistance, and push-pull force.
kg/s^2
Newton
Kg m^2 / s^2
Joule, or Newton - meter
Kg / s^2
Spring constant, K, or N / m
FV
Power, valid only for constance forces. It is also equal, also equal to work / time.
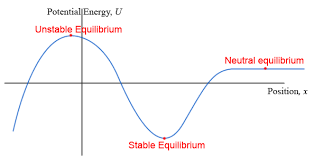
Stable Equilibrium
This is a point where an object, if displaced slightly from its equilibrium position, experiences a force that tends to bring it back to the equilibrium position. The potential energy here is at a minimum.
It appears as a valley on a potential energy graph
Ex. a ball at rest in a bowl.
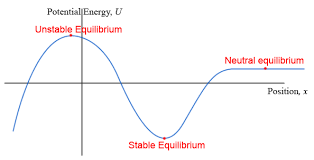
Unstable Equilibrium
This is a point where, if the object is displaced even slightly, the force acting on it will drive it further away from the equilibrium position. The potential energy here is at a maximum.
It appears as a peak on a potential energy graph.
Ex. a ball balanced on a steep hill.
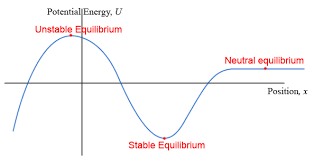
Neutral Equilibrium
These are locations where the potential energy curve is completely flat, so if the particle is given a little nudge, it will continue to move with a constant velocity.
Bound System
in terms of potential energy is one where the object or particle is confined to a specific region due to the nature of the potential energy. The object cannot move to a position where the U(x) curve is greater than the mechanical energy because this would require that it have a negative kinetic energy, which is impossible.
The system typically has a stable equilibrium with minimum potential energy, and the object cannot escape this region unless it gains enough energy to overcome the potential barrier.
Ex: gravitational systems (planet orbiting a star), springs and oscillations.
Critical Angle
Huh
Work in Circular Motion
In a circle at constant speed, the work done is zero since the Force is always perpendicular to the distance moved as you move incrementally around the circle
impulse
change in momentum = (integral of F)t dt
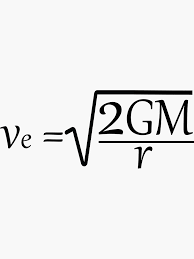
Escape Velocity
This is the minimum speed required for an object to escape the gravitational pull of a planet without any further propulsion.
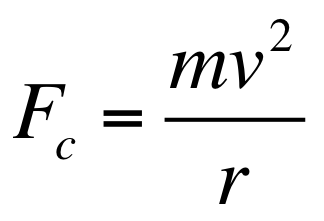
Centripetal Force
This is the sum of forces in the radial direction. Ex. if a ball is at the bottom of the circle, Fc is equal to tension - gravity.
Velocity of the Center of Mass of a System
Given by the sum of the momentums of the individual objects divided by the total mass.
When momentum is conserved between the objects in a system, the velocity of the center of mass stays constant and there is no acceleration of the center of mass.
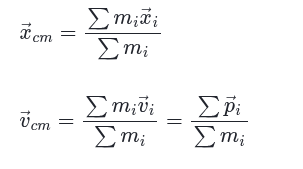
Inertial Mass
This refers to an object's resistance to changes in its motion, or its "inertia". A more massive object requires a greater force to achieve the same acceleration as a less massive object. It is measured by applying a force and observing the resulting acceleration (F=ma
Gravitational Mass
This describes the strength of an object's gravitational interaction with other objects, or how strongly it is pulled by gravity. It's measured by comparing the gravitational force exerted on an object to the gravitational force exerted on a known mas
T = dL / dt
Net torque is equal to the change in angular momentum over the change in time.
Resonance
This occurs when an external force is exerted at the natural frequency of an oscillating system. It increases the amplitude of oscillating motion. The natural frequency of a system is the frequency at which the system will oscillate when it is displaced from its equilibrium position.
Natural Frequency
This is the frequency at which the system will oscillate when it is displaced from its equilibrium position.
Period
In SHM, this is equal to 1 / f or 2pi / w (angular frequency)
Ts = 2pi sqrt(m/k)
Period of Oscillator
Tp = 2pi sqrt( L / g )
Period of Pendulum
x = A cos (2 pi ft) or x = A sin (2 pi ft)
Displacement of object in simple harmonic motion.
A = -w^2x
Acceleration of an object in simple harmonic motion.
Vmax = Aw, amax = Aw^2
Maximum velocity and maximum acceleration of an object in simple harmonic motion.
Physical Pendulum
A simple pendulum is an ideal model, consisting of a point mass suspended from a massless, inextensible string, while a BLANK is a real object, like a rod or any rigid body, oscillating about a fixed axis.
T = 2pi sqrt(1/mgd)
Period for a physical pendulum.
t = -mgd sin(theta)
When displaced from equilibrium, the gravitational force exerted on a physical pendulum’s center of mass provides a restoring torque
I x angular acceleration = -k(theta)
A torsion pendulum is a case of SHM where the restoring torque is proportional to the angular displacement of a rotating system. For example, a horizontal disk that is suspended from a wire attached to its center of mass may undergo rotational oscillations about the wire in the horizontal plane. Equation for torque:
W = integral t d(theta)
Work done by a torque
L = r x p, L = mvr sin(theta)
The angular momentum of an object/particle about a given point:
impulse = integral of torque dt
Angular Impulse
A x B = AB cos(theta)
Dot product of vectors
F net = dp / dt = m (dv / dt) = (dm / dt) v
The rate of change of a systems momentum is equal to the net external force exerted.
Fnet = -du/dx
The conservative forces exerted on a system in a single dimension can be determined using the slope of the system’s potential energy with respect to position in that dimension; these forces point in the direction of decreasing potential energy.
Lambda = dm/dx
Linear mass density of a rod (lambda) is the derivative of mass with respect to the length (x)
M = integral of density p( r )dV
If a function of mass density is given for a solid, the total mass can be determined by integrating the mass density over the length (one dimension), area (two dimensions), or volume (three dimensions) of the solid.
m = 4/3 p (r^3)
Partial mass of a sphere = volume of that particular part x density
Use the radius of the partial sphere
V = sqrt (gr)
At the top of a vertical, circular loop, an object requires a minimum speed to maintain circular motion. At this point, and with this minimum velocity, the gravitational force is the only force that causes the centripetal acceleration.
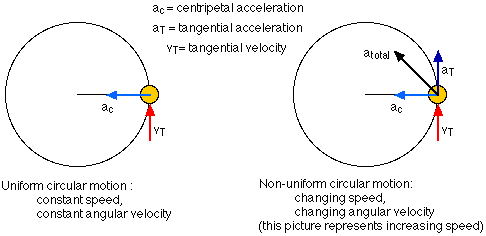
The net acceleration of an object moving in a circle is the vector sum of the centripetal acceleration and tangential acceleration.
T = (2pi r) / v
For an object traveling at a constant speed in a circular path, the period is given by the derived equation
T^2 = ((4pi^2) / GM) r^3
For a satellite in circular orbit around a central body, the satellite’s centripetal acceleration is caused only by gravitational attraction. The period and radius of the circular orbit are related to the mass of the central body