AB Calculus - Theorem Definitions

This set includes all theorems from Units 1, 5, and 6 of AB Calculus and how they can be used.

Squeeze Theorem

If g(x) ≤ f(x) ≤ h(x), and if the limit of g(x) as x approaches the constant value a equals the limit of g(x) as x approaches a, then the limit of f(x) as x approaches a will also equal the limit of f(x) and g(x) as x approaches a.

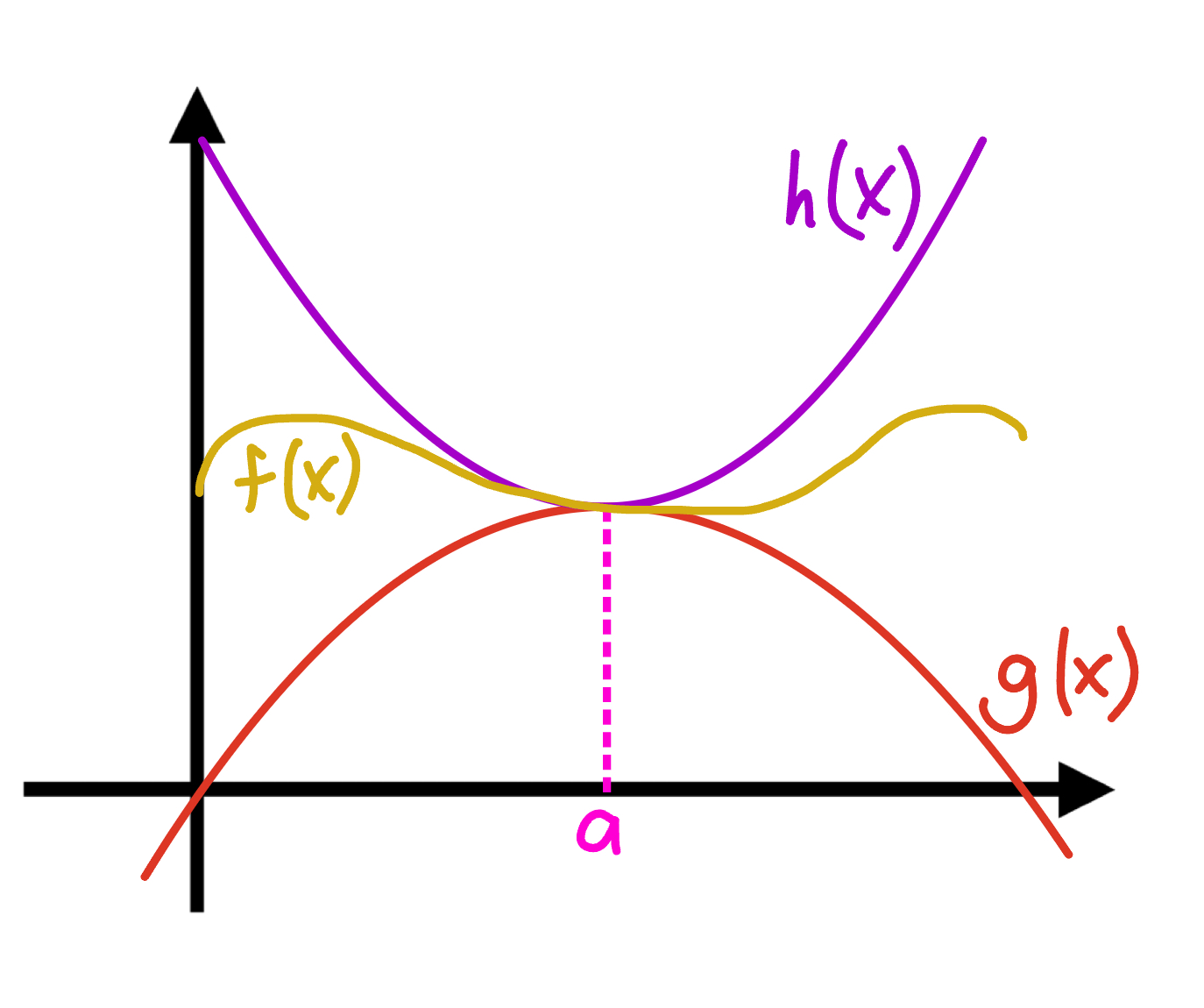
How can we use the Squeeze Theorem?

We can use it to determine the limit of an unknown function if we are given two known functions that are less than or equal to each other.

Intermediate Value Theorem

If the function f(x) is continuous from a to b, then every value between f(a) & f(b) exists at some point on the interval [a,b].

How can we use the Intermediate Value Theorem?

We can use it to determine if a certain value occurs on an interval of a function, given a table of values and it’s stated that the function is continuous.

Mean Value Theorem

If the function f(x) is continuous over the interval [a,b] and differentiable over the interval (a,b), then there exists a point c within that open interval where the instantaneous rate of change equals the average rate of change over the interval.

How can we use the Mean Value Theorem?

To determine when the average rate of change is equal to the instantaneous rate of change.

Average rate of change equation

This equation generates the slope of the secant line at two points on a function.

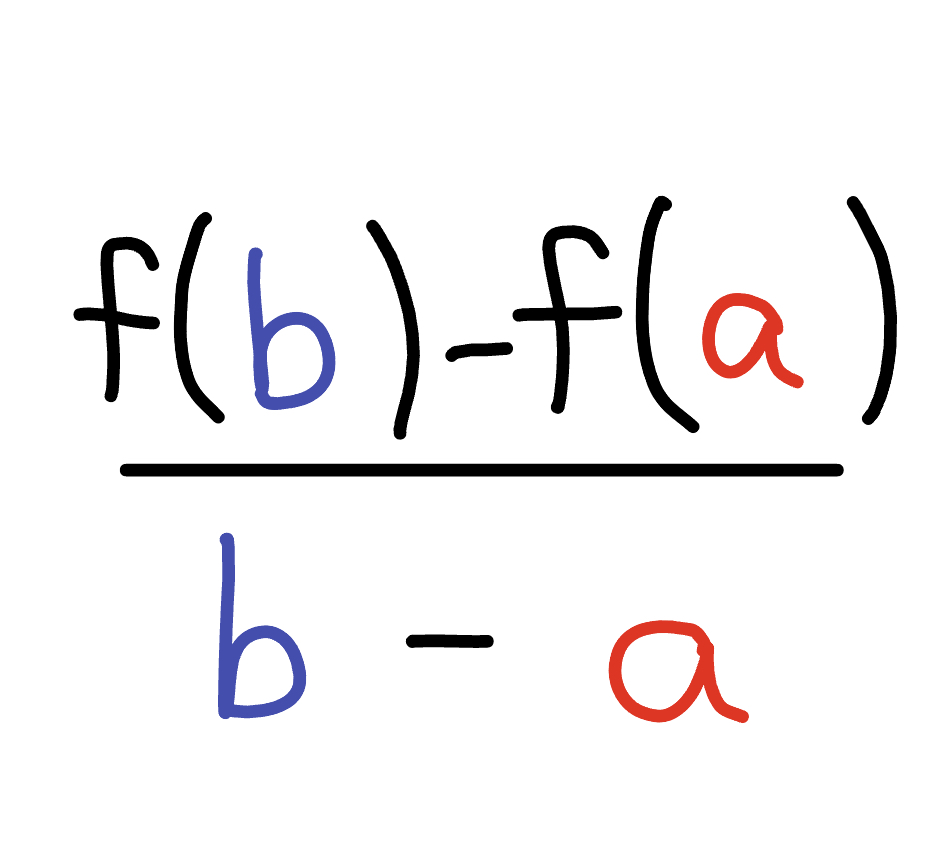
Instantenous rate of change equation

This equation generates the slope of the tangent line at a point on a function.

Extreme Value Theorem

If the function f(x) is continuous over the interval [a,b], then f has at least one minimum value and at least one maximum value on [a,b].

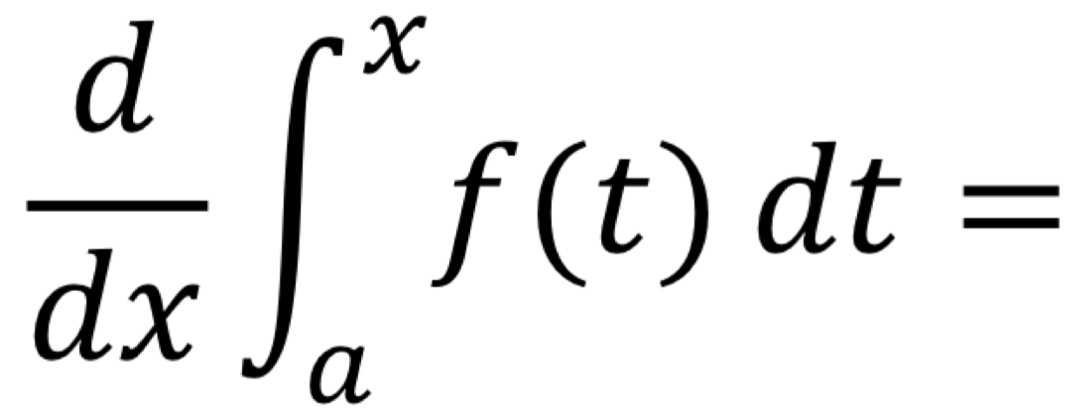
The Fundamental Theorem of Calculus | If a is a constant and f(t) is a continuous function, then…

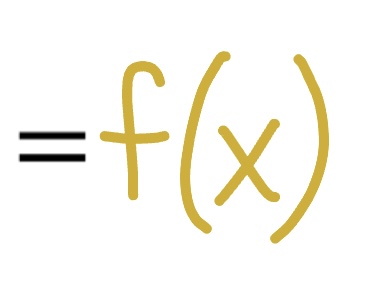
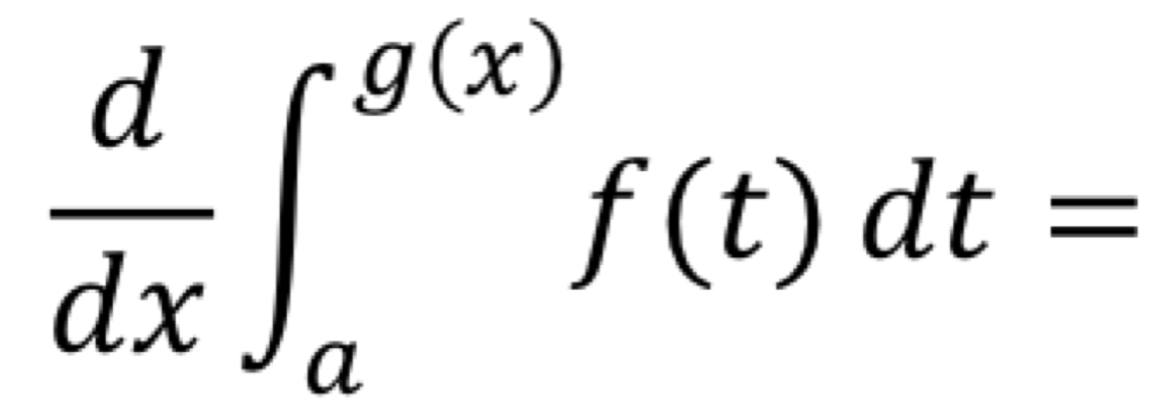
The Fundamental Theorem of Calculus | If a is a constant and f(x) is a continuous function, what is the result when one limit of integration is a function, and we take the derivative of the integral expression?

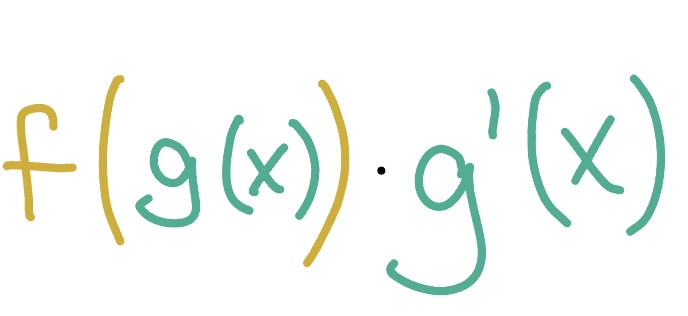
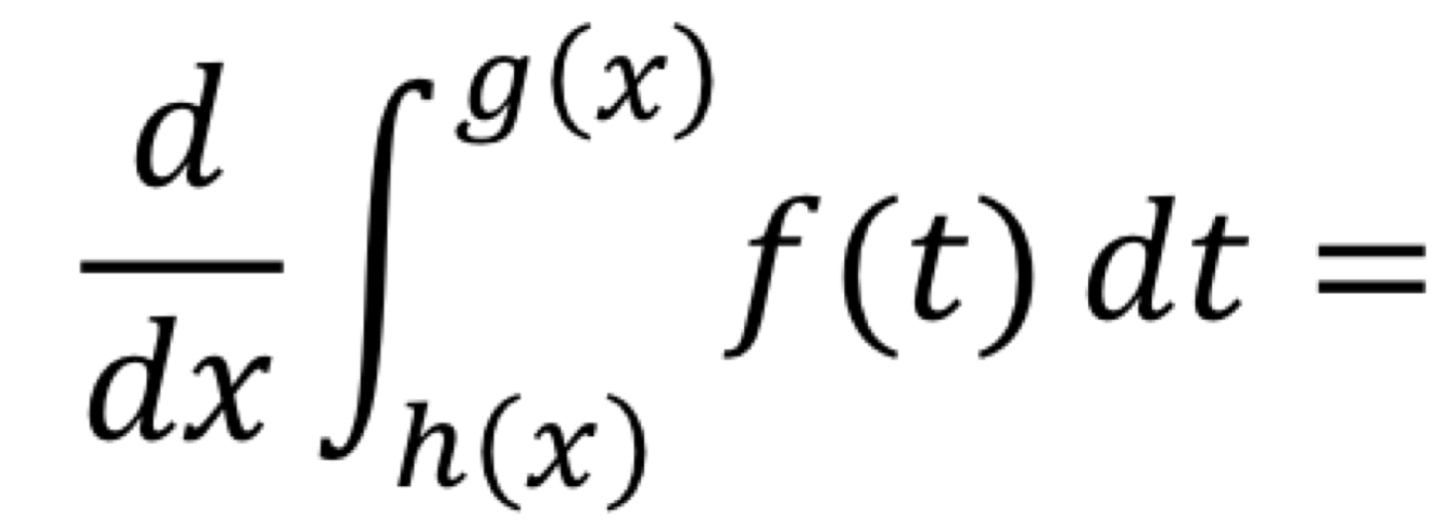
The Fundamental Theorem of Calculus | What is the result when both limits of integration are functions, and we take the derivative of the integral expression?

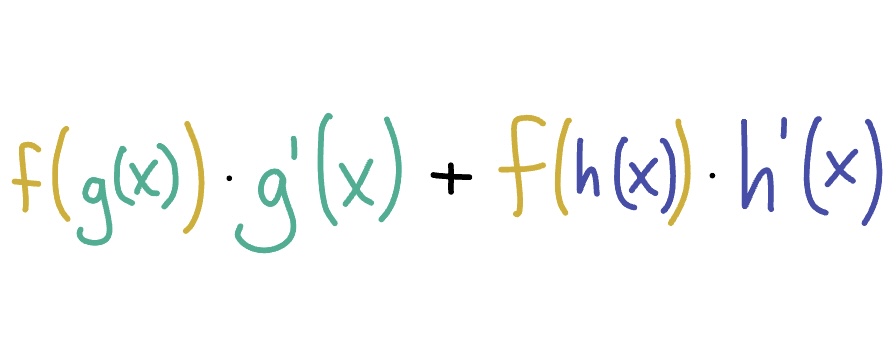
The Fundamental Theorem of Calculus | Area

If the function f(x) is continuous over the interval [a,b], then the area under the curve of f(x) from [a,b] can be represented by the following equation…