AP Precalculus Unit 1 Review

Flashcards covering multiple choice questions from AP Precalculus Unit 1.

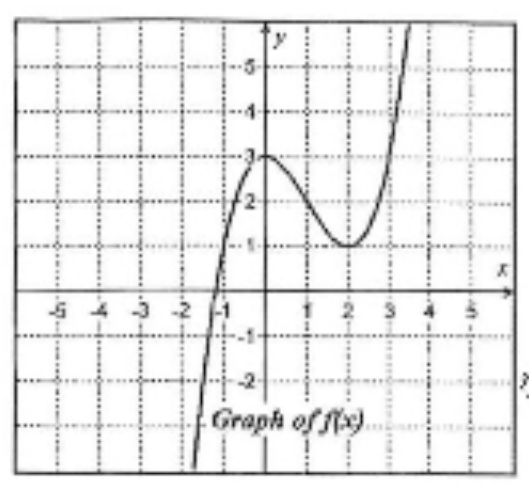
On what open intervals is the graph of f decreasing at an increasing rate?

From (0, 2)

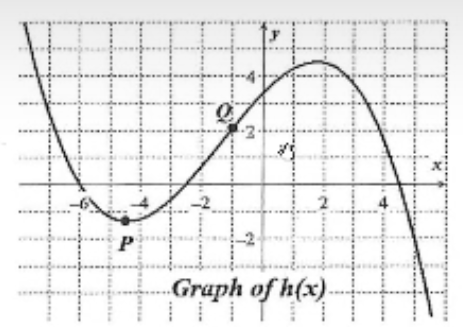
On what intervals is the average rate of change of g the greatest? (refer to table with x and g(x) values)

From (3, 6)

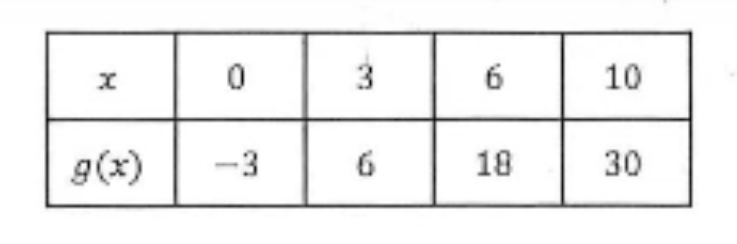
Describe the behavior of the graph of h(x) from point P to point Q. (refer to the Graph of h(x))

Increasing at an increasing rate

What is the average rate of change of g over the interval 0 < x < 5?

-1

For a cubic function f, the rate of change is positive at x = -4, negative at x = 1, and positive at x = 4. Where are the max/min points on the graph of f?

Local maximum between (-4, 1), and a local minimum between (1, 4)

A salesperson earns $4.00 commission for the first $10,000 of sales and then $200 for each additional $10,000 or partial. What is S(75,000)?

1304

Which function has two vertical asymptotes, one horizontal asymptote, and no holes?

B

If (2, 4) is on the graph of y = j(x), find a point on the graph of y = j(x + 2) + 2.

(0,6)

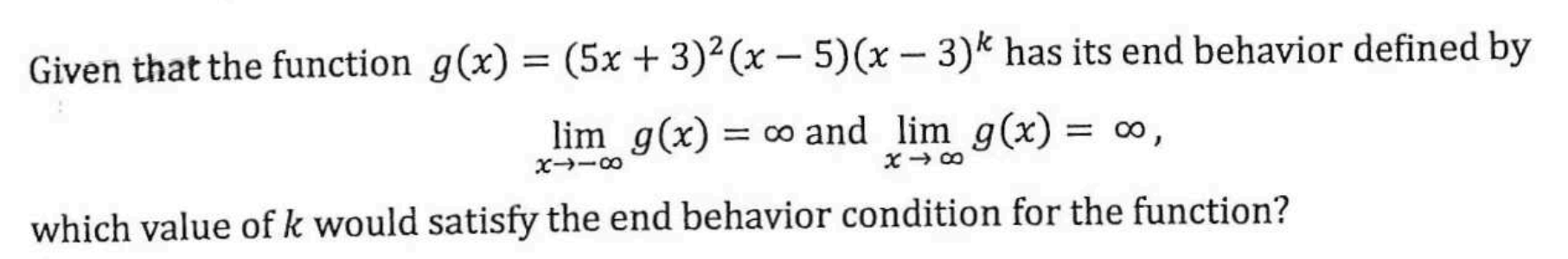
1

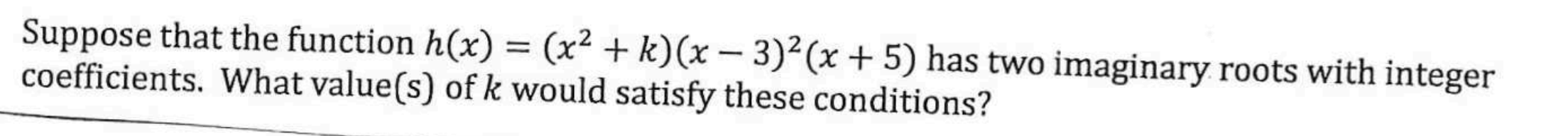
k > 0

What is the coefficient of x in the expansion of (2x + 5)³?

150

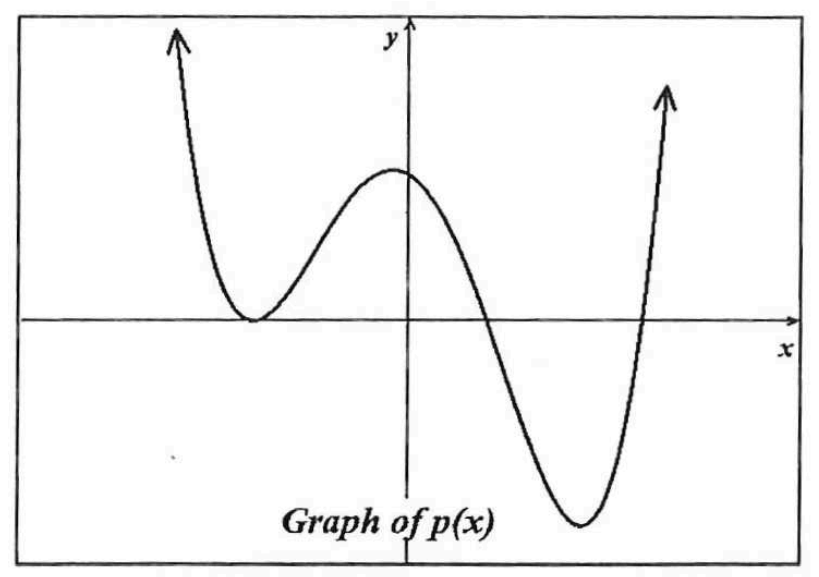
Given the graph of the polynomial function p, what could be an expression for P(x)?

3 real polynomials

Let h(x) = -2x^2 (x + 2)(x - 3). What are all the intervals for which f(x) > 0

(-2, 0) union (0, 3)

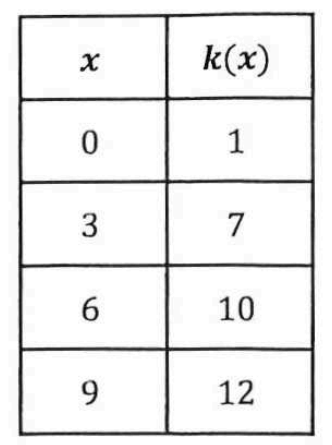
Selected values of the polynomial k are shown in the table. Which claim and explanation statements could be true about k(x)?

B, Concave up Increasing

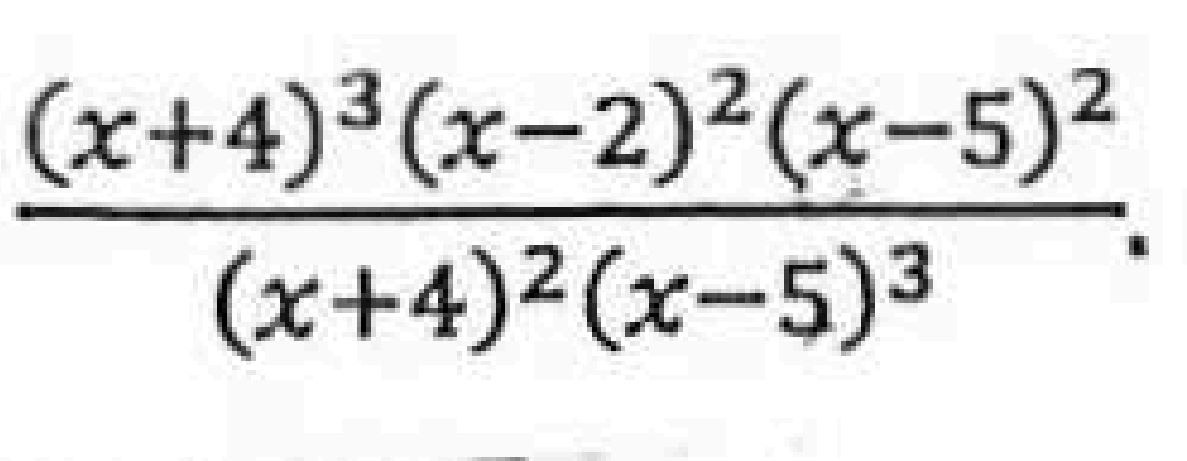
The graph of f has a zero at what values of x?

-4 and 2

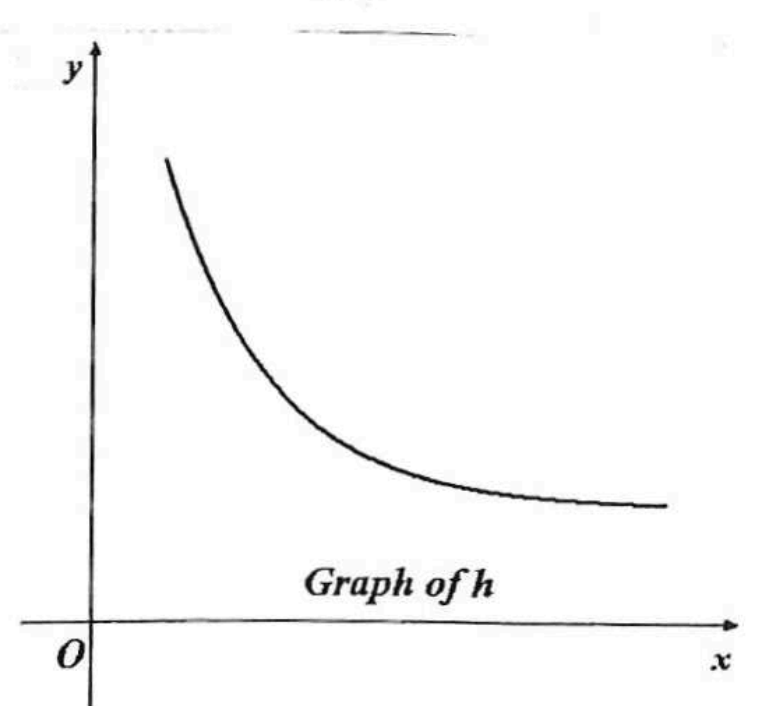
Given the graph of the function h(x), write a statement about the rate of change of h.

decreasing at an increasing rate

The rational function r is given by r(x) = (x^2+8x+16)/(x^2-8x+16). Which statements are true about r?

Based on r(x)=(x+4)^2/(x-4)^2 one concludes: Vertical asymptote at x=4. Horizontal asymptote at y=1. Removable discontinuity: None.

Given the graph of the rational function R(x), what could be the expression for R?

Based on the provided information, you would need the graph of R(x) to answer this question. Without the graph, a definitive answer cannot be given.

Let f(x) = x^2 + 8x + 4 and g(x) = 2x^2 + 5x - 6. Find all intervals on which g(x) > f(x).

First, solve for when g(x) = f(x), so 2x^2+5x-6 = x^2+8x+4 -> x^2-3x-10 = 0 -> (x-5)(x+2) = 0,
so the solutions are x=5 and x=-2.
Now, since g(0) = -6 and f(0) = 4, g(x)g(x) on the interval (-inf,-2) U (5,inf).

Given the graphs of the functions f(x) and g(x), what is an expression for g(x) in terms of f(x)?

Based on the provided information, you would need the graph of f(x) and the graph of g(x) to answer this question. Without the graphs, a definitive answer cannot be given.

The functions f and g are defined for all real numbers such that g(x) = f(2 + x). What transformation maps the graph of f to the graph of g in the xy-plane?

The transformation is a horizontal shift of 2 units to the left.

What type of function would be the most appropriate to model the relationship between x and y for this dataset, and why?

Based on the provided information, you would need the dataset to answer this question. Without the dataset, a definitive answer cannot be given.

Let h be a polynomial function whose graph has a point of inflection at x = 4. Which of the following statements about h must be true?

The graph of the rate of change of h has a relative extremum at x = 4.

A nature preserve has 1,400 feet of fencing to enclose a rectangular flamingo habitat, with one side along a river requiring no fencing. Express the area of the habitat A as a function of x.

Let x be the length of the sides perpendicular to the river, and y be the length of the side parallel to the river.
The perimeter is 2x + y = 1400, so y = 1400 - 2x.
The area A = x * y = x(1400 - 2x) = 1400x - 2x^2.
A(x) = 1400x - 2x^2

The function y = f(x) has a domain of -7 < x < 12 and a range of -4 < y < 6. What is the range of the transformation g(x) = f(x - 3) + 4?

The transformation represents a vertical shift of 4 so the range becomes (-4+4, 6+4)=(0, 10).

Which interval contains two zeros for the rational function m given by m(x) = (x + 3)(x - 2)(x + 5)(x - 7) / (x + 5)(x - 3)?

The zeros are at x = -3, 2, and 7. The removable discontinuity is at x = -5. We need a calculator to specify exactly which range is given.

Meghan keeps track of her charitable contributions. The table shows how her contributions have changed over the past few years. What was the average annual increase between 2019 and 2022?

Based on the provided information, you would need the table of values to answer this question. Without the table, a definitive answer cannot be given.

A ball is launched upwards with an initial velocity of 155 feet per second. The distance in feet of the ball from the ground after t seconds is D(t) = 155t - 16t^2. For what interval of time is the ball more than 278 feet above the ground?

Based on the provided information, you would need a calculator to answer this question. Without the calculator, a definitive answer cannot be given.

Let f be the function given by f(x) = 7^x / (1 + 3^x). Which Statement is true?

Based on the provided information, you would need a calculator to answer this question. Without the calculator, a definitive answer cannot be given.

The function given by g(x) = (x - 5)(x^2 + 4x + 3) / ((x - 5)(x - 2)) has a hole where x = 5. Which of the following is lim x->2 g(x)?

Based on the provided information, you would need a calculator to answer this question. Without the calculator, a definitive answer cannot be given.

The rational function R is given by R(x) = (1.92x^2 + 2.8x - 2.5) / (1.6x^2 - 6.41x + 3.35). At what x-values does the graph of R(x) have a hole?

Based on the provided information, you would need a calculator to answer this question. Without the calculator, a definitive answer cannot be given.

The table provides values of f(x) for values near x = 3. Which of the following is true for f?

Based on the provided information, you would need the table to answer this question. Without the table, a definitive answer cannot be given.

The function V gives the traffic flow in a 24-hour period. The table gives the number of vehicles V(t) for selected values of t, in hours, for 0 < t < 24. A quartic regression is used to model these data. What is the value of V(19) predicted by the quartic function model?

Based on the provided information, you would need a calculator to answer this question. Without the calculator, a definitive answer cannot be given.