Mathematics FRQ's Marquez

AP PRECALCULUS

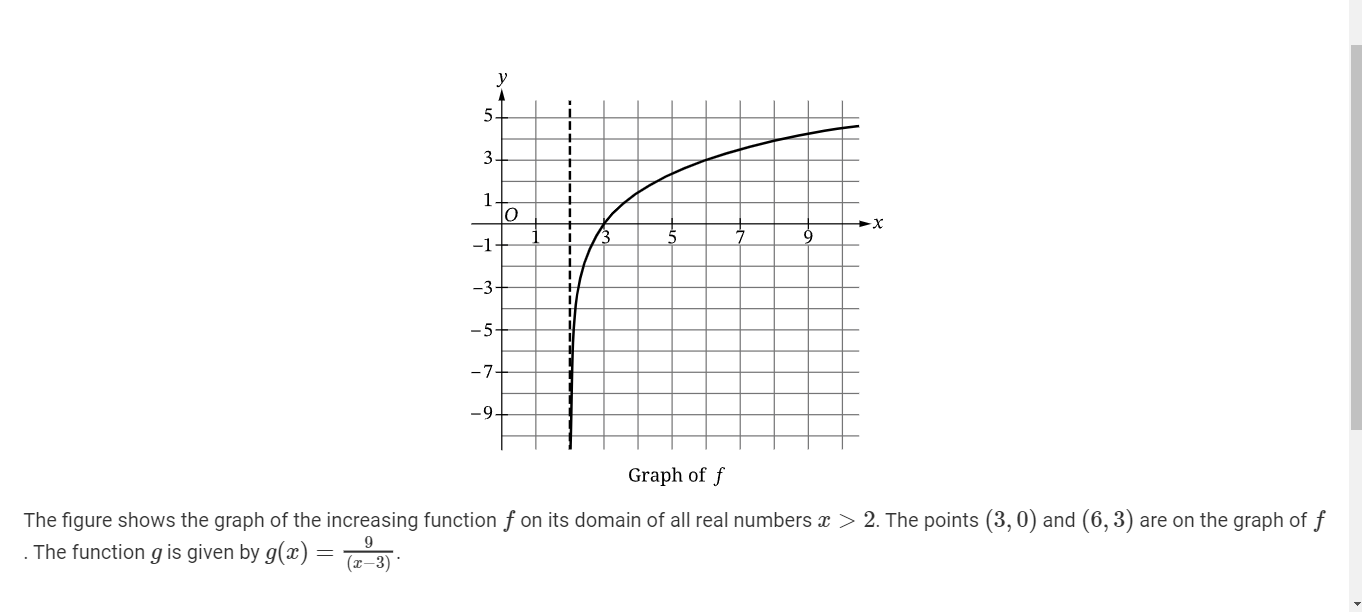
A(i) The function h is defined by h(x)= g(f(x)). Find the value of h(6) as a decimal approximation, or indicate that it is not defined? (CALCULATOR)

It’s definitely undefined. because when f(6) we get 3 and if you input it onto the equation you get 9/0 which is undefined.

A(ii) Find all real zeros of f, or indicate there are no real zeroes. (CALCULATOR)

The only real zero is 3 because when 3 is the only one on the x axis. You could also deduce this by knowing that (3,0), and (6,3)

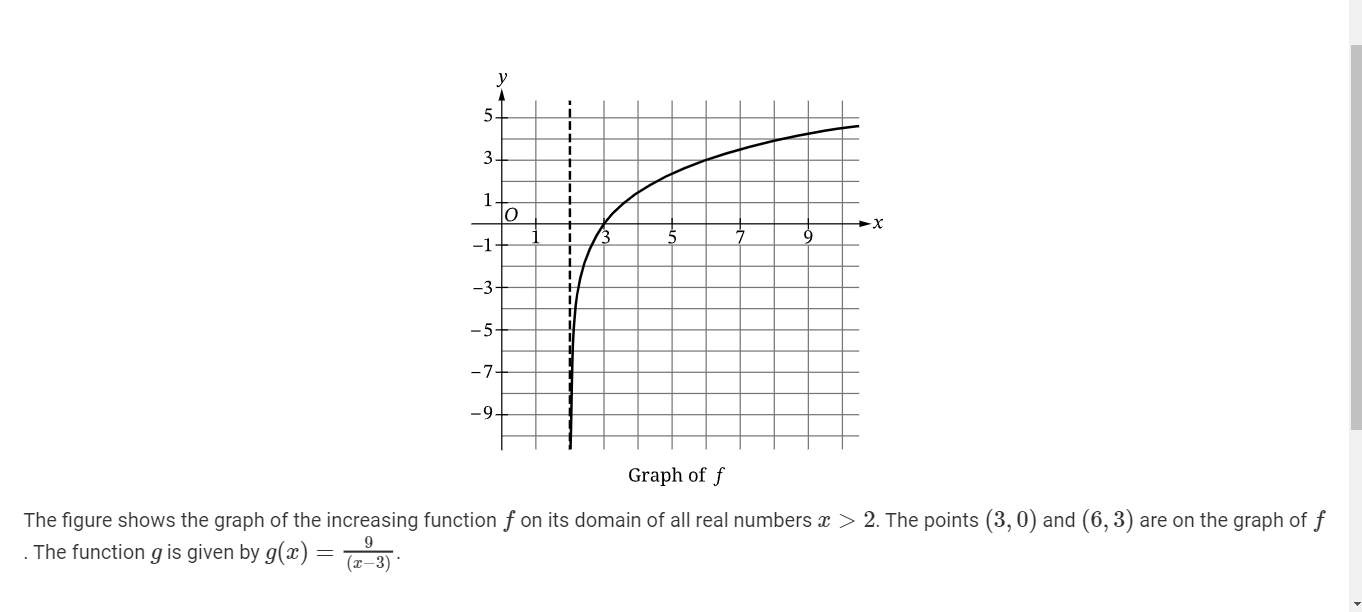
(Bi) Find all of values of x, as decimal approximations, for which g(x)=-5.8, or indicate that there are no such values.

The answer is about 1.448

EXPLANATION

9/(x-3) = -5.8

9=-5.8 (x-3)

9/-5.8 about -1.552

-1.552+3 is about 1.448.

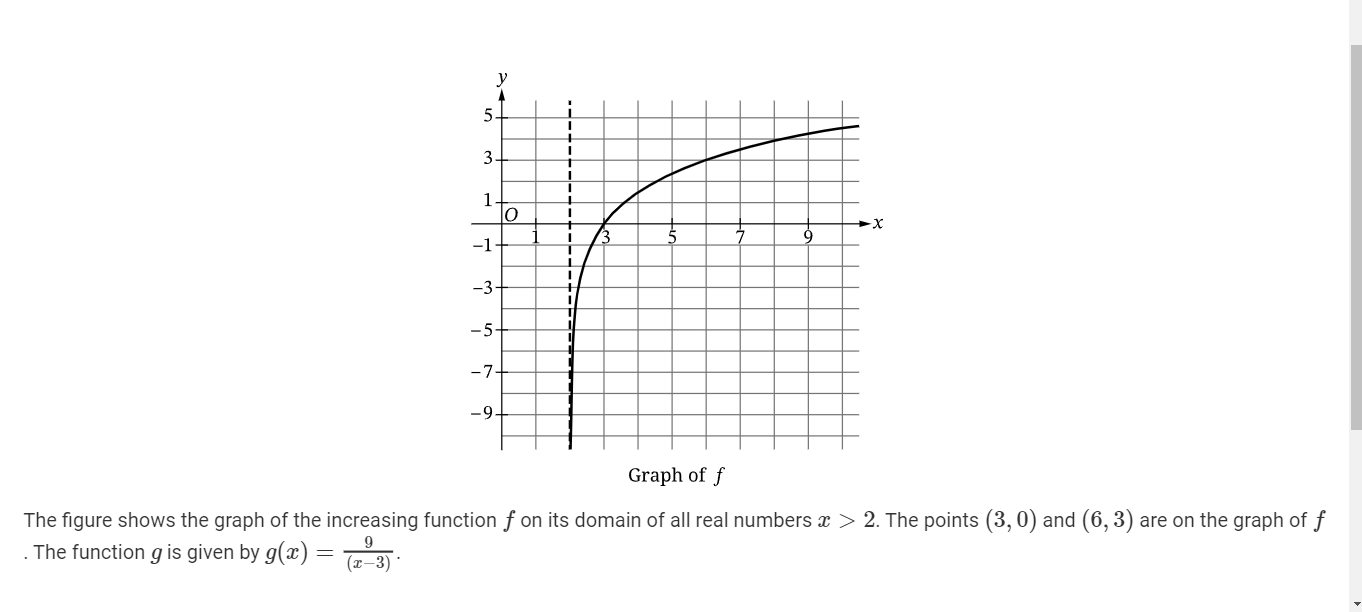
B(ii) Determine the end behavior of g as x decreases without bound. (CALCULATOR)

lim g(x)=0

x →

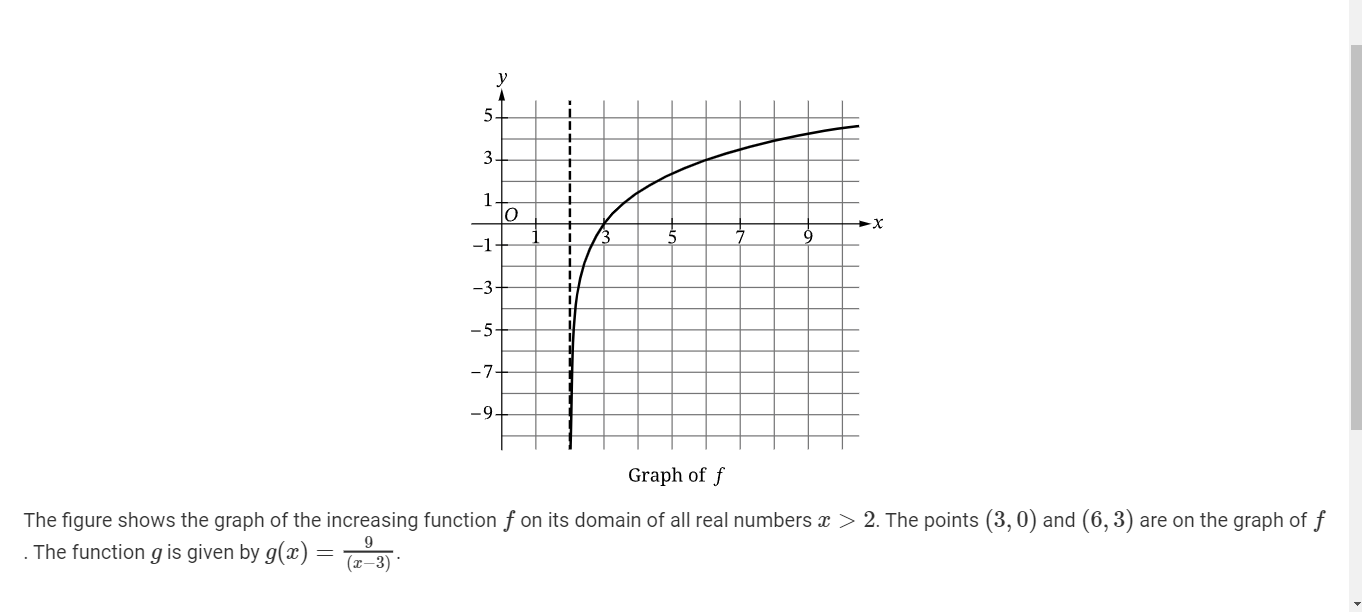
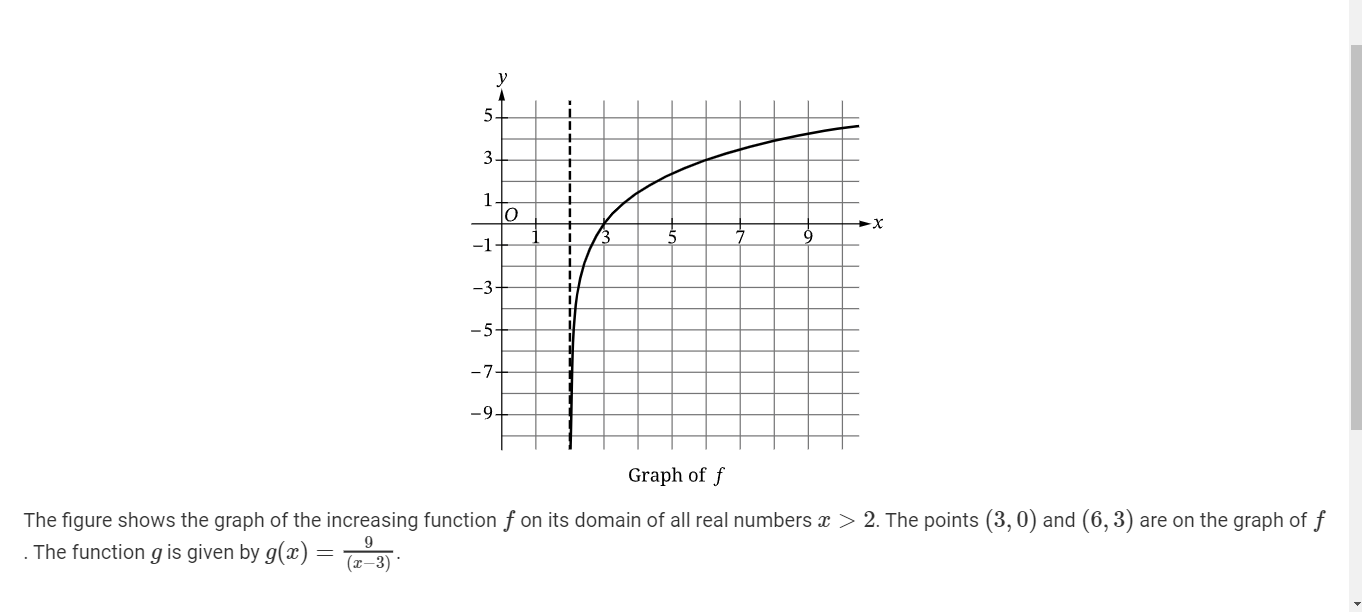
C (i) Determine if f is invertible (Calculator)

Yes it is.

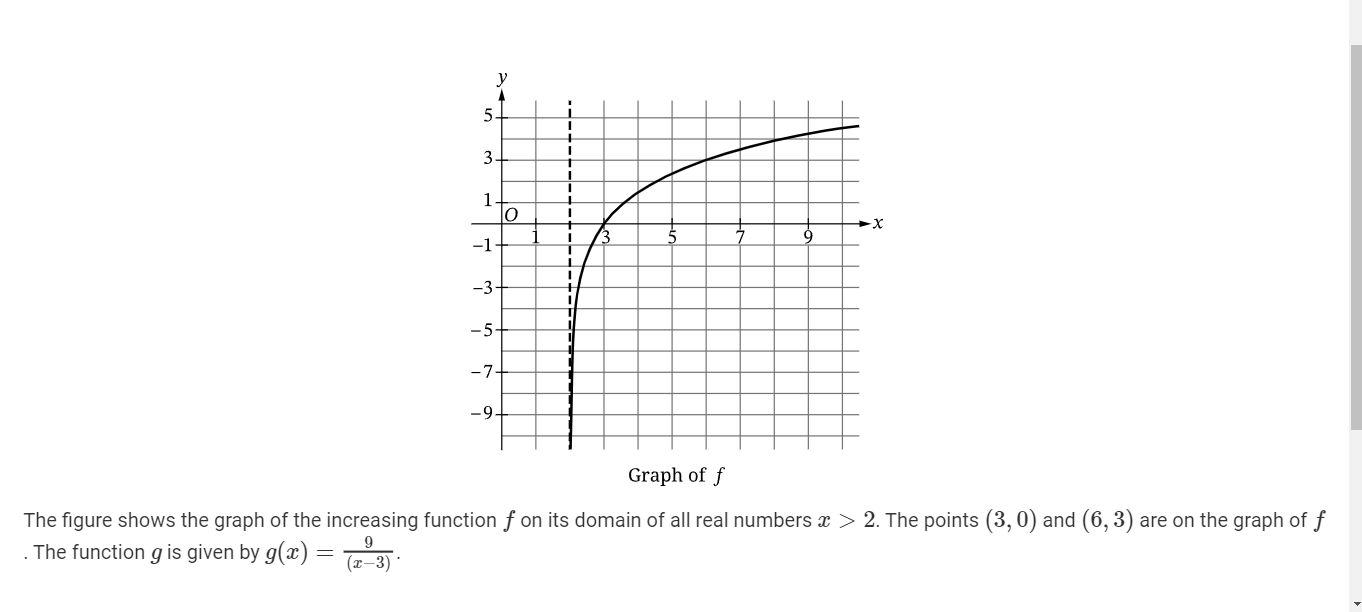
C (ii) Give a reason for your answer based on the definition a function and the graph of y = f(x).

I believe that f is invertible because it contains a unique value (y) for every x value.

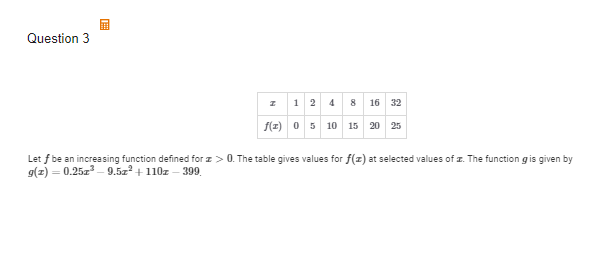
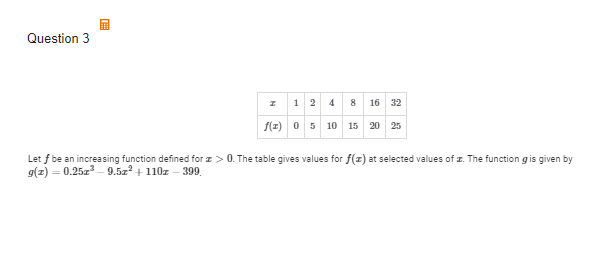
A(i) The function h is defined by h(x)=g(f(x)). Find the value of h(4) as a decimal approximation, or indicate that it is not defined.

(i) = The Value of h(4) is approximately 2.197 because when f(4)= 3 and 3 you input in the log equation which gives us about 2.197.

A(ii) Find all values of x for which f(x)=3, or indicate that there are no such values.

(ii) = The value of when x=2 and x=4 yields to f(x)=3.

B(i) Find all values of x, as decimal approximations, for which g(x)=, or indicate that there are no such values.

4.481 or 4.482. Divide 2 by both sides, you get In (x)= 3/2. Remember that log base e argument x is the equivalent so technically we can convert it to a exponential so, e^3/2 is about 4.481 or 4.482.

B(ii) Determine the end behavior of g as x increases without bound. Express your answer using the mathematical notation of a limit

lim g(x)= infinity

x → Infinity

C(i) Determine if f has an inverse function.

Nope, it does not have an inverse.

C(ii) Give a reason for your answer based on the definition of a function and the table of values of f(x).

(ii) The reason why I don't believe so is because x=2 and x=4 has same range so that disqualifies it automatically.

A(i) The function h is defined by h(x)= g(f(x)). Find the value of h(8) as a decimal approximation, or indicate that it is not defined.

(i) -42.75 (You insert 15 to the equation).

A(ii) Find the value of f ^-1 (20), or indicate that it is not defined.

(ii) x= 16 because if (16,20) the inverse is (20,16)

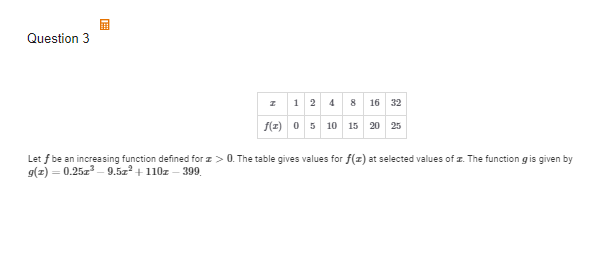
B(i) Find all values of x, as decimal approximations, for which g(x)= -45, or indicate there are no such values.

(i) x= 5.321, x= 15.410, x= 17.269. In the graphing calculator input this equation but add 45 so you don't leave any y value.

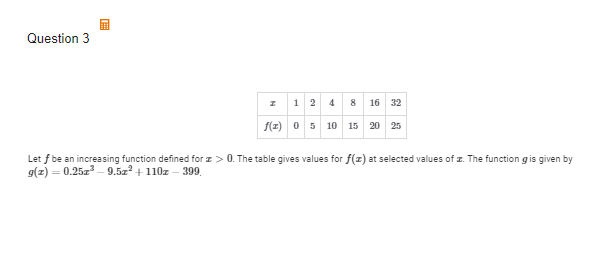
B(ii) Determine the end behaivor of g as x increases without bound.

(ii) lim g(x)= infinity

x ---> infinity

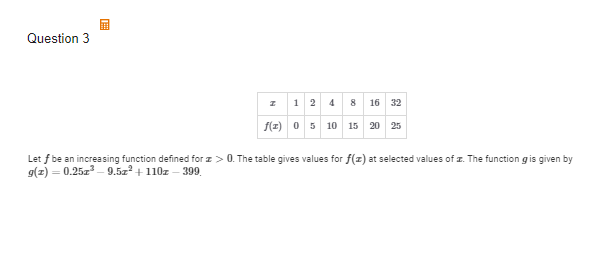
C(i) Use the table of values of f(x) to determine if f is best modeled by a linear, quadratic, exponential, or log function

log function.

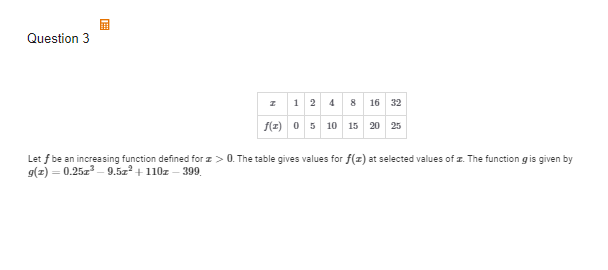
C(ii) Give a reason for your answer based on the relationship between the change in the output values of f and the change in the input values of f.

(ii)The x values are changing proportionally as y increases in equal lengths.

A (i) Use the given data to write two equations that can be used to find the values for constants a and b in the expression for P(t)

(i) The equations are ab^2= 59 and ab^8= 118

A(ii) Find the values for a and b as decimal approximations(ii)

(ii) A is about 46.83 and B is about 1.122.

B (i) Use the given data to find the average rate of change of the number of plants, in plants per year, from t=2 to t=8 years. Express your answer as a decimal approximation. Show the computations that lead to your answer.

(i) The approximation is about 9.833 plants per year.118-59/8-2 yields about 9.833 plants per year.

B (ii) Use the average rate of change found in (i) to estimate the number of plants for t=10 years. Show the work that leads to your answer.

(ii) I believe that the answer is about 137 or 138. We can estimate when t=10 by using y1+slope(x-x1). 59+9.8333(10-2) is about 137 or 138.

B (iii) The average rate of change found in (i) can be used to estimate the number of plants during year t, for t > 10 years. Are these estimates, found using the average rate of change, less than or greater than the number of plants predicted by the model P during year t, for t > 10 years? Explain ur reasoning.

(iii) Based on the information given, I believe that average rate of change is less than than the number of plants predicted by the model. The reason why I believe this is because in the first place, this function exhibits a concave up shape. it should be noted that it goes to infinity and the secant line that passes through the 2 points (which make the slope) is fixed. So the estimates using the average rate of change are actually less than predicted of that of the model.

C (i) In which t-value, t=6 years or t=20 years, should the ecologist have more confidence when using the model P? Give a reason for your answer in the context of the problem.

I believe that the ecologist should have a more confidence with t=6. The reason why I believe this to be true is because it falls within the domain that we are given. Additionally, we don't actually know what could be the maximum so having confidence in t=20, might be a bad idea.

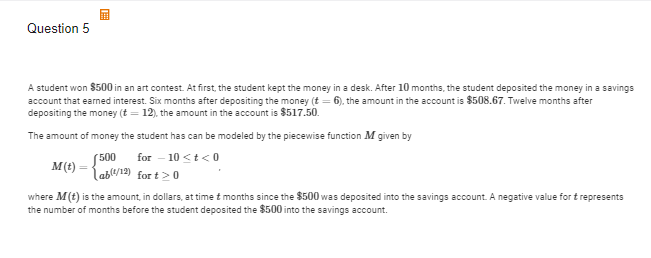
A(i) Use the given data to write two equations that can be-used to find the values for constants a and b in the expression for M(t)

ab^(0/12) = 500, ab^(6/12)= 508.67, ab^(12/12)=517.50

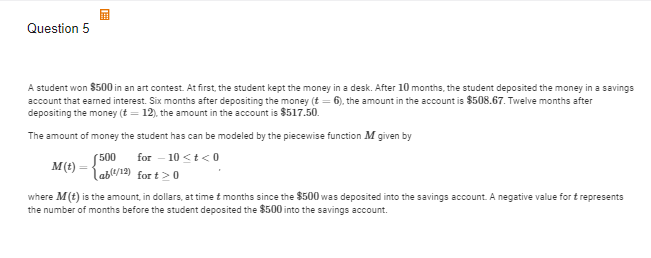
A(ii) Find the values for a and b as decimal approximations.

Because M(0) = 500, ab^0 = 500 so A has to be 500. 500 x b^1/2=508.67 so b = 1.034981.

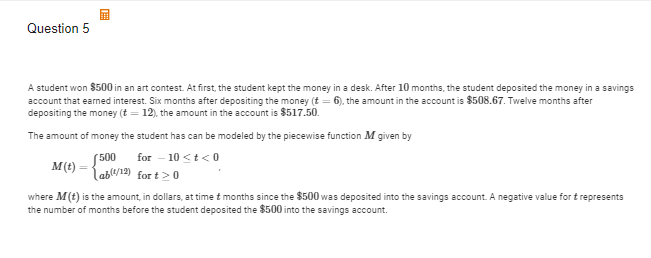
B(i) Use the given data to find the average rate of change of the amount of money the student has, in dollars per months, from t=-2 to t= 12 months. Express your answer as a decimal approximation. Show the computation that lead to your answer.

(517.50 - 500)/14 = 1.25. The average rate of change is 1.25 dollars per month.

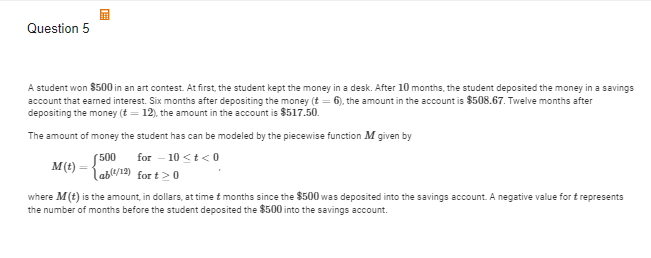
B(ii) Use M(12) and the average rate of change found in (i) to estimate the amount of money, in dollars, the student has when t=20 months. Show the work that leads to your answer.

y= M(12) + r (x-12). x=20

y=517.50 + r (20-12) = 527.50

The amount of money the students has when t=20 was approximately 527.50 dollars.

B(iii) Let A(t) be the estimate of the amount of money, in dollars, the student has a time at t months using the average rate of channge found in (i). In (ii) A(20) was computed. If A(t) is used to estimate values for M(t) for t>12, the error in the estimates will increase as t increases. Explain why this is true.

The estimate A(t) is the y- coordinate of a point on the secant line that passes through (-2,M(-2)) and (12,M(12)). Because the graph of M is concave up for t >_0 (and constant for t < 0), this line is below the graph of M for t> 12. Therefore, the estimate using the Average rate of change A(t) is less than the value of M(t) for t > 12.

C(i) The student plans to close the account when the amount of money in the account reaches $565. Explain how this information can be used to determine the domain limitations for the model M.

$565 is the desired amount of money in the account. The account will be closed at time Tc months when M(Tc)= 565. Therefore, the domain of M is limited to -10 < t < tc months. (In this situation, tc= 42.632.)

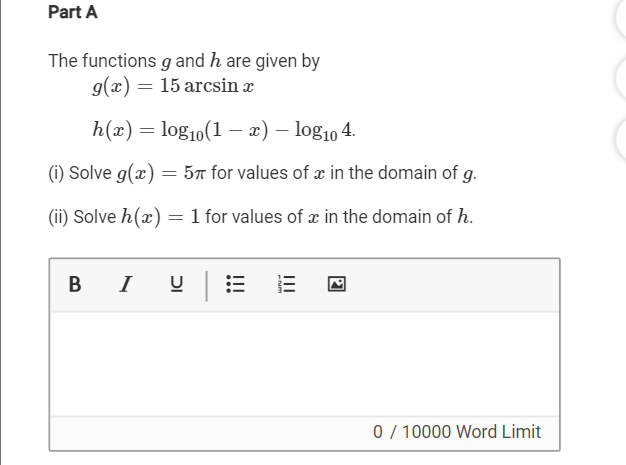
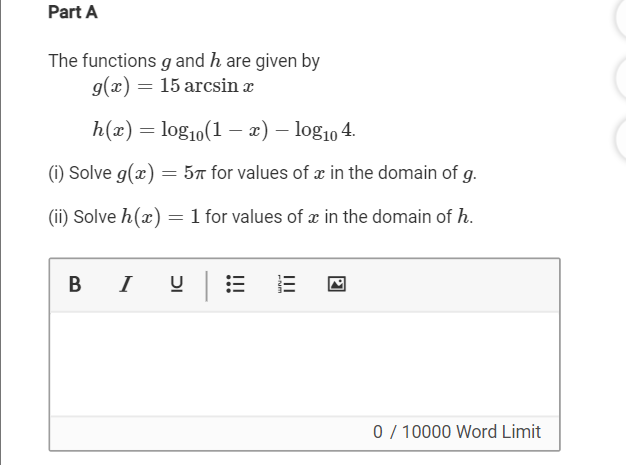
A(i) Solve g(x) = 5pi for values of x in the domain of g.

Step 1: Set up the equation= 15 arcsin (x)= 5pi

Step 2: Divide 5pi/15

Step 3: arcsin x = 5pi/15

Step 4 determine what is x= sin (pi/3) with special right triangles.

x= (Square root of 3)/2

A(ii) Solve h(x) = 1 for values of x in the domain of h.

Step 1: Set up the equation: Log (1-x) - log (4) = 1

10 10

Step 2: convert to exponential: (1-x/4)=10

Step 3: Isolate x. 1-x = 40.

X= - 39.

B(i) Rewrite j(x) as a single logarithm base 2 without negative exponents in any part of the expression. Your result should be of the form log2(expression)

B(ii) Rewrite k(x) as a fraction involving powers of cos x and no other trigonometric function

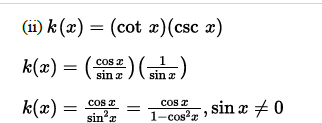
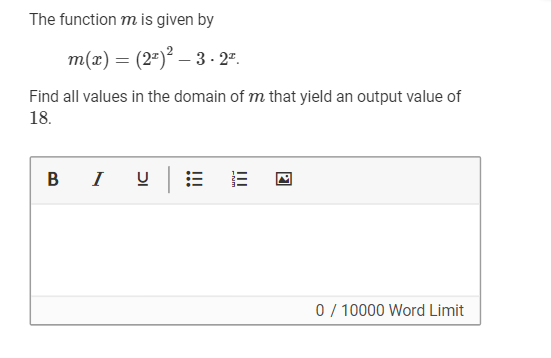
C(i) Find all values in the domain of m that yield an output value of 18?

A(i) Solve g(x)= 3 for values of x in the domain of g

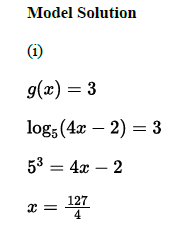
A(ii) Solve h(x) = Pi/4 for values of x in the domain of h.

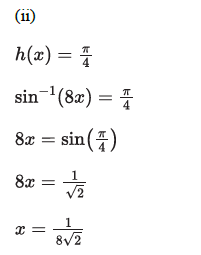
B(i) Rewrite j(x) as an expression involving sin x and no other trig function.

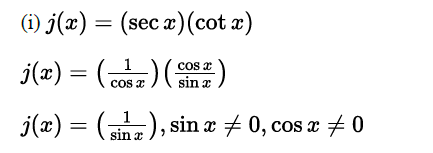
B(ii) Rewrite k(x) as an expression of the form 4^(ax+b), where a and b are constants.

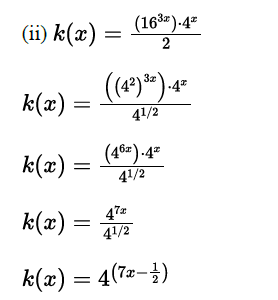
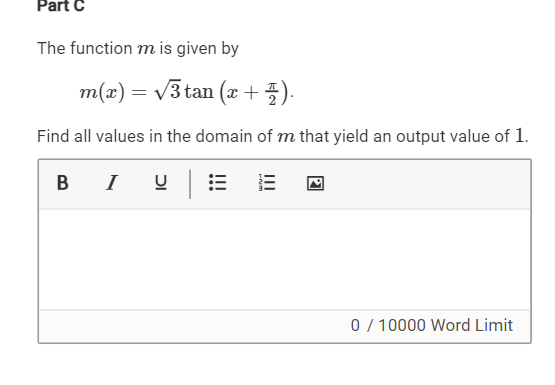
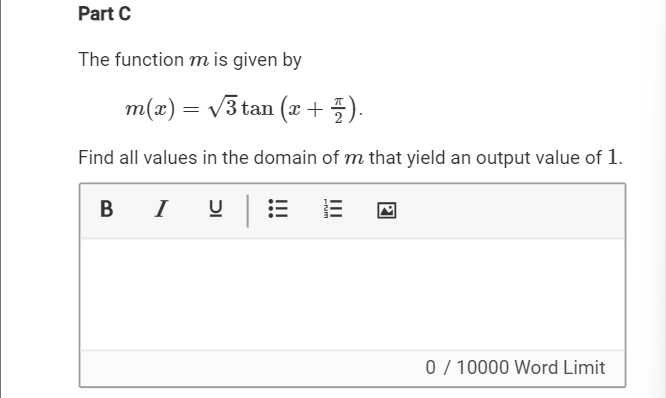
C(i) Find all values in the domain of m that yield an output value of 1.

B(i) Use the given data to find the average rate of change of the scores, in points per month, from 𝑡=0 to 𝑡=3 months. Express your answer as a decimal approximation. Show the computations that lead to your answer.

R(3)-R(0)/3-0 = -1.387

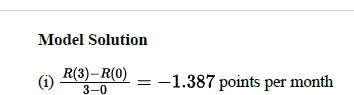
B(ii) Interpret the meaning of your answer from (i) in the context of the problem.

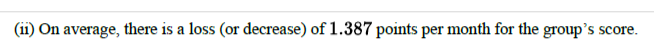
B(iii) Consider the average rates of change of 𝑅 from 𝑡=3  to 𝑡=𝑝 months, where 𝑝>3. Are these average rates of change less than or greater than the average rate of change from 𝑡=0 to 𝑡=3 months found in (i)? Explain your reasoning.

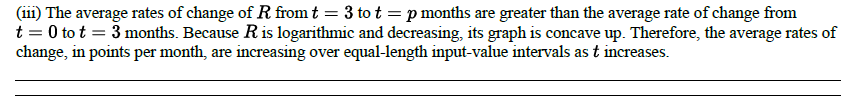
(i) Use the given data to write three equations that can be used to find the values for constants 𝑎, 𝑏, and 𝑐 in the expression for I(t)

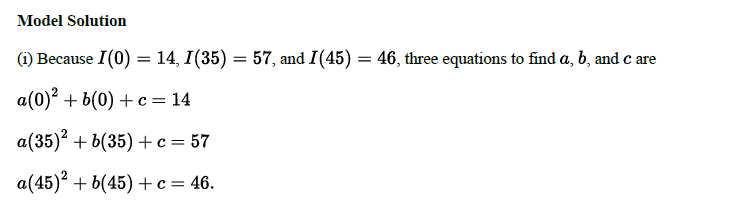
(ii) Find the values for 𝑎,  𝑏, and 𝑐 as decimal approximations.

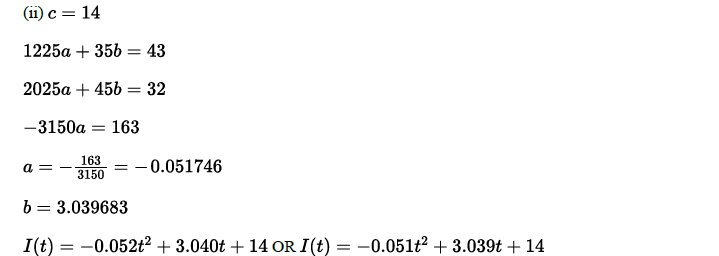
(i) Use the given data to find the average rate of change of the number of ice cream cones sold, in cones per day, from 𝑡=35 to 𝑡=45 days. Express your answer as a decimal approximation. Show the computations that lead to your answer.

(ii) Use the average rate of change found in (i) to estimate the number of ice cream cones sold on day 𝑡=40. Show the work that leads to your answer.

Explain how the range values of the function 𝐼 should be limited by the context of the problem.

Explain how the range values of the function 𝐼 should be limited by the context of the problem.

(i) On the interval (𝑡1,𝑡2), which of the following is true about h ?

1. h is positive and increasing.

2. h is positive and decreasing.

3. h is negative and increasing.

4. h is negative and decreasing.

Choice A

(ii) Describe how the rate of change of h is changing on the interval (𝑡1,𝑡2).

The graph of ℎ and its dashed midline for two full cycles is shown. Five points, 𝐹, 𝐺, 𝐽, 𝐾, and 𝑃, are labeled on the graph. No scale is indicated, and no axes are presented.

Determine possible coordinates 𝑡,ℎ𝑡 for the five points: 𝐹, 𝐺, 𝐽, 𝐾, and 𝑃.

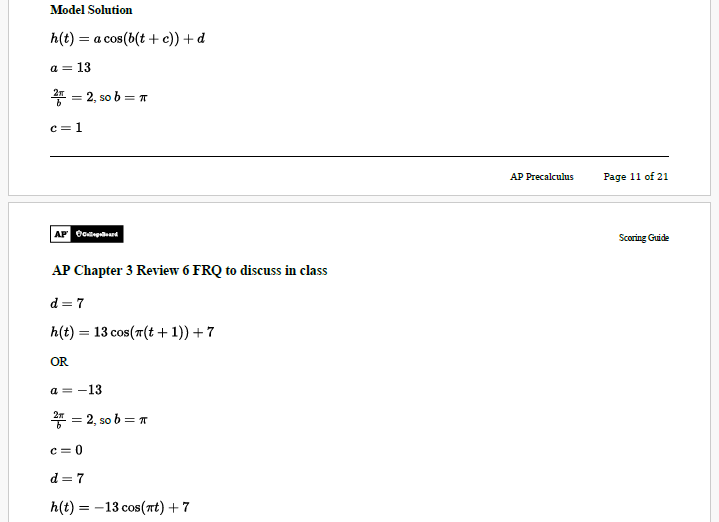
The function ℎ can be written in the form ℎ𝑡=𝑎cos𝑏𝑡+𝑐+𝑑. Find values of constants 𝑎, 𝑏, 𝑐, and 𝑑.

Refer to the graph of ℎ in part (A). The 𝑡-coordinate of 𝐽 is 𝑡1, and the 𝑡-coordinate of 𝐾 is 𝑡2.

(i) On the interval 𝑡1,𝑡2, which of the following is true about ℎ ?

     a. ℎ is positive and increasing.

     b. ℎ is positive and decreasing.

     c. ℎ is negative and increasing.

     d. ℎ is negative and decreasing.

Choice C

(ii) Describe how the rate of change of ℎ is changing on the interval 𝑡1,𝑡2.

The graph of ℎ and its dashed midline for two full cycles is shown. Five points, 𝐹, 𝐺, 𝐽, 𝐾, and 𝑃, are labeled on the graph. No scale is indicated, and no axes are presented.

Determine possible coordinates 𝑡,ℎ𝑡 for the five points: 𝐹, 𝐺, 𝐽, 𝐾, and 𝑃.

The function ℎ can be written in the form ℎ𝑡=𝑎sin𝑏𝑡+𝑐+𝑑. Find values of constants 𝑎, 𝑏, 𝑐, and 𝑑.

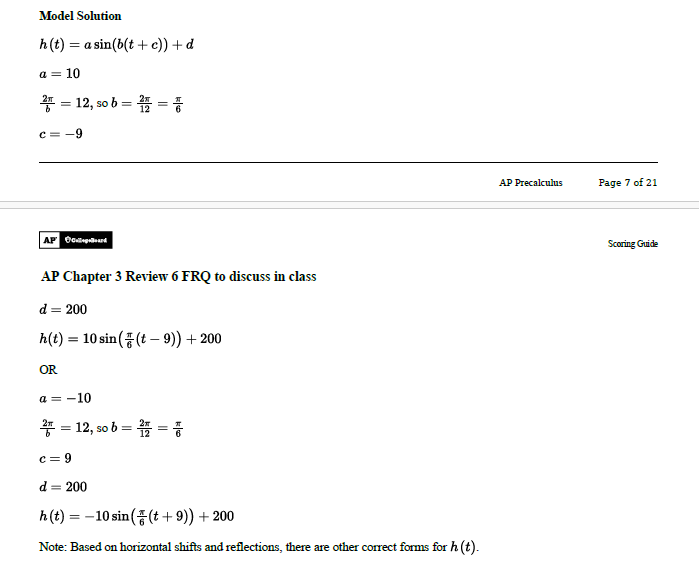
Refer to the graph of ℎ in part (A). The 𝑡-coordinate of 𝐽 is 𝑡1, and the 𝑡-coordinate of 𝐾 is 𝑡2.

(i) On the interval 𝑡1,𝑡2, which of the following is true about ℎ ?

     a. ℎ is positive and increasing.

     b. ℎ is positive and decreasing.

     c. ℎ is negative and increasing.

     d. ℎ is negative and decreasing.

Choice A

(ii) Describe how the rate of change of ℎ is changing on the interval 𝑡1,𝑡2.

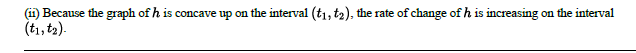
The graph of ℎ and its dashed midline for two full cycles is shown. Five points, 𝐹, 𝐺, 𝐽, 𝐾, and 𝑃, are labeled on the graph. No scale is indicated, and no axes are presented. Determine possible coordinates 𝑡,ℎ𝑡 for the five points: 𝐹, 𝐺, 𝐽, 𝐾, and 𝑃.

The function ℎ can be written in the form ℎ (𝑡)=𝑎cos(𝑏(𝑡+𝑐))+𝑑. Find values of constants 𝑎, 𝑏, 𝑐, and 𝑑.

(i) On the interval (𝑡1,𝑡2), which of the following is true about ℎ?

1. ℎ is positive and increasing.

2. ℎ is positive and decreasing.

3. ℎ is negative and increasing.

4. ℎ is negative and decreasing.

Choice A

(ii) Describe how the rate of change of ℎ is changing on the interval (𝑡1,𝑡2).

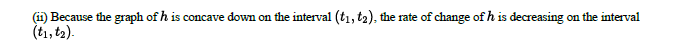
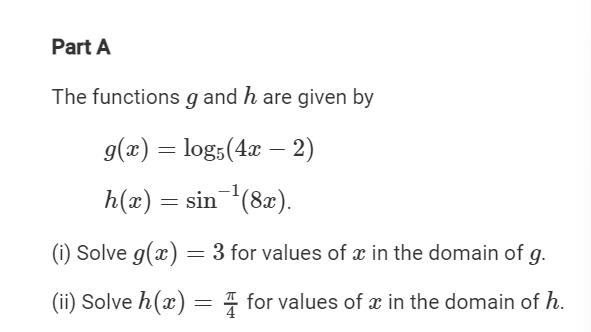
(i) Solve 𝑔𝑥=3 for values of 𝑥 in the domain of 𝑔.

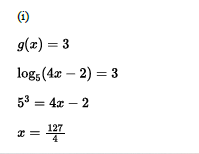
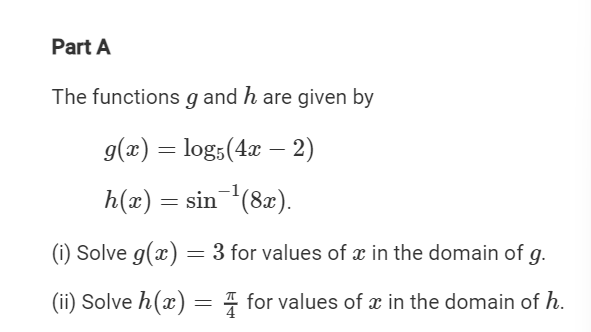
(ii) Solve ℎ𝑥=𝜋/4 for values of 𝑥 in the domain of ℎ.

(i) Rewrite 𝑗 (𝑥) as an expression involving sin 𝑥 and no other trigonometric functions.

Rewrite 𝑘(𝑥) as an expression of the form 4(𝑎𝑥+𝑏), where 𝑎 and 𝑏 are constants.

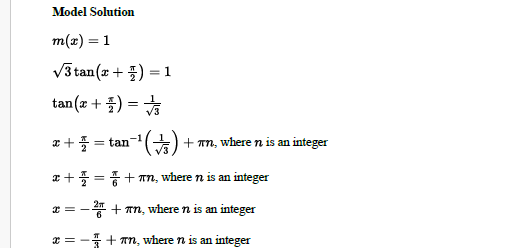
(i) Solve 𝑔𝑥=5𝜋 for values of 𝑥 in the domain of 𝑔.

(ii) Solve ℎ𝑥=1 for values of 𝑥 in the domain of ℎ.

(i) Rewrite 𝑗𝑥 as a single logarithm base 2 without negative exponents in any part of the expression. Your result should be of the form log2 expression.

(ii) Rewrite 𝑘𝑥 as a fraction involving powers of cos𝑥 and no other trigonometric functions.

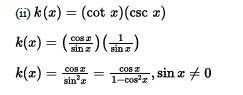
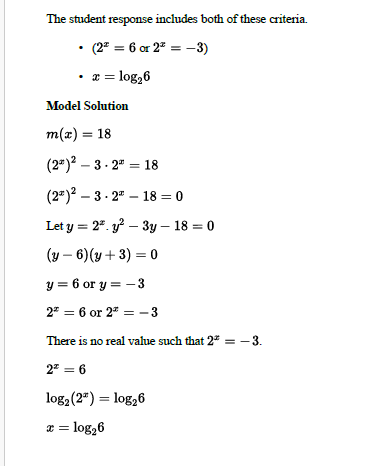
(i) Solve 𝑔𝑥=3 for values of 𝑥 in the domain of 𝑔.

(ii) Solve ℎ𝑥=𝑒1/2 for values of 𝑥 in the domain of ℎ

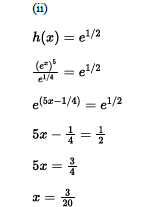
(i) Rewrite 𝑗𝑥 as a single logarithm base 10 without negative exponents in any part of the expression. Your result should be of the form log10expression.

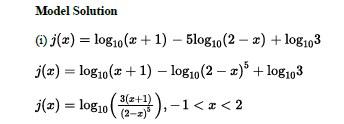
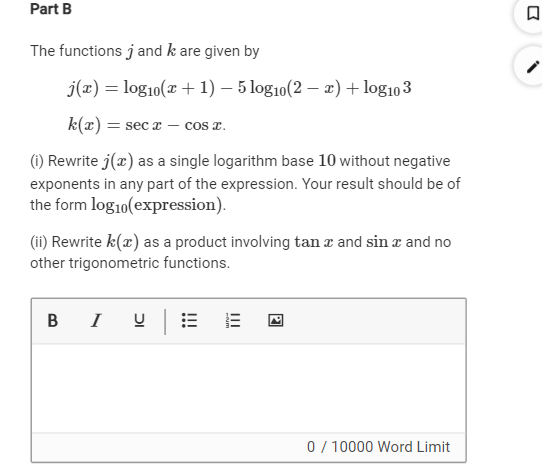
(ii) Rewrite 𝑘(𝑥) as a product involving tan𝑥 and sin𝑥 and no other trigonometric functions.

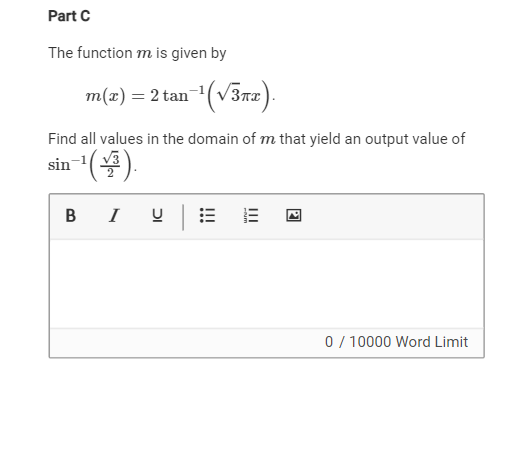
Find all values in the domain of 𝑚 that yield an output value of sin-1 (Square root of 3)/2