Ch 1A - Rn and Cn
1/28
Earn XP
Description and Tags
Introduction to vector spaces Rn and Cn. Do not test on multiple choice or true or false.
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
29 Terms
The study of linear maps on finite-dimensional vector spaces Rn:
Linear algebra
A set with arithmetic rules that satisfy natural algebraic properties:
Vector space
The set of all complex numbers C is denoted by the expression:
a+bi; a,b in R
What set is denoted by the expression “α + βἱ: α,β in R”?
Complex numbers C
“α + β = β + α” is what property of complex arithmetic?
commutativity
“(α + β) + λ = α + (β + λ )” and “(α β) λ = α (β λ)” are what property of complex arithmetic?
associativity
“λ + 0 = λ” is what property of complex arithmetic?
additive identity
“λ 1 = λ” is what property of complex arithmetic?
multiplicative identity
For every α in C, there exists a unique β in C such that “α + β = 0”. What property of complex arithmetic is this?
additive inverse
For every α in C with α ≠ 0, there exists a unique β in C such that “α β = 1”. What is this property of complex arithmetic?
multiplicative inverse
“λ (α + β) = λ α + λ β”, where all variables are complex numbers. What is this property of complex arithmetic?
distributive property
What does the vector space F stand for?
Either R or C
When emphasizing that an object is a number, not a vector, we call it an element of F. What is another term for this number?
scalar
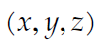
A ____ of length n is an ordered collection of n elements
list
It is the number of elements within a list
length
What do we call elements separated by commas and surrounded by parentheses?
list
T or F: A list may have infinite length.
F
T or F: Order matters and repetitions have meaning for lists
T
T or F: sets work the same as lists, the only difference is their annotation
F
T or F: For sets, order and repetitions are relevant
F
Consider the set x in Fn, what does “xk” stand for? (where κ is a number from 1 to n)
kth coordinate from x1 to xn
It is the kth position within a list x in Fn, a number from 1 to n.
coordinate
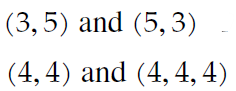
T or F: Two lists are equal even if they do not share the same length or the elements are out of order
F
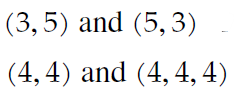
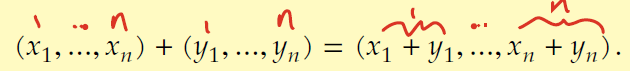
It is defined by adding the corresponding kth coordinate
Addition in Fn
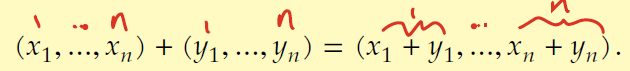
If x, y are elements of Fn, then “x + y = y + x”. What is the name of this property?
commutativity of addition in Fn
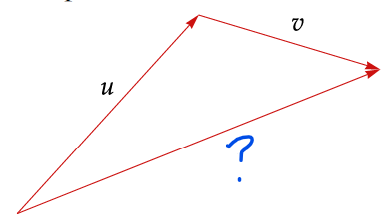
What does this illustration help visualize?
The sum of two vectors
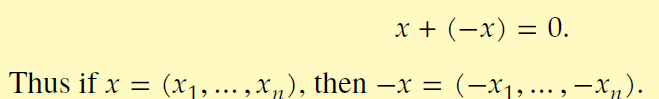
For x in Fn, there exists a vector -x (in Fn) such that x + (-x) = 0. What is this the definition to?
additive inverse in Fn
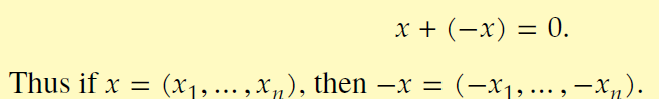
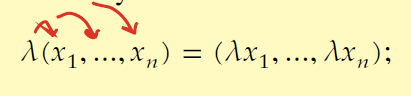
__________ is defined as multiplying each coordinate of a vector x by a scalar λ
scalar multiplication in Fn
It is a set containing at least two distinct elements called 0 or 1, along with operations of addition and multiplication satisfying all properties of complex arithmetic. Examples of it are C and R.
field