RMDA Final Exam

Surveys

Method of gathering information from participants via self report

Can be used for frequency or association claims

Can be used to capture attitudes/judgments

Survey validity

Dependent on:

1. Feasibility

Ex. Studying infants, cant ask them to talk

2. The questions themselves

Are questions neutral or do they lead participants to an answer

Types of questions

1. Open-ended

2. Forced-choice

3. Likert scale

Open-ended

Allows the participant to fill in the response in any way they like

Trouble: Ability to condense what they’re saying to analyze/code

Good for:

1. Sensitive or socially disapproved behaviors Ex. Drinking or sexual behaviors

2. Research questions on explicit content of a self-generated response or information implicit in reponse Ex. Use of language

3. Preliminary Research

Forced-choice

The participant is given a limited set of options and must choose one

Anytime they give you a label at the end its forced choice (Ex. Personality quiz)

Disadvantage:

People might not know what category they belong in

Lose “richness” lose more talking

Good for:

1. Easily analyzed

2. Auto-scored

Likert scales

Provide a range of forced-choice responses that are ratings

Could be 1-5, stars, strongly agree to strongly disagree, etc

Ex. Amazon ratings and psych evals

-Individually: Ordinal

-Mean of several: Interval

Disadvantages of forced-choice

Ex. What is the most important social issue today

• abortion

• Healthcare

• schools

• energy

Particiants would pick one, but when open-ended they rarely bring those things up

Question wording

Both the strucutre and the wording can implicitly suggest a range of appropriate answers

Can ask the same question worded slightly differently and get different responses

Ex. Not allowing vs. forbidding

Can impact witness testimony

Questions to avoid

Leading questions, double-barreled questions, negatively worded questions, question order

Leading questions

Type of question in a survey/poll thats wording encourages only one response

Ex. How would you rate the legendary Reds player Pete Rose?

Double-barreled questions

Type of question in survey/poll that asks two or more questions in one

Ex. Do you feel it is worth an additional expense to provide internet connectivity to cardio machines to have additional features of workout tracking, social media, and video streaming

Negatively worded questions

Type of question in survey/poll that contains negatively phrased statements, making its wording complicated or confusing

Ex. Rate extend to which you agree or disagree that students should never go to class

Question order

Question order biases later responses

Which of these four activities are your favorite ways to exercise? Walking, biking, running

How often do you exercise in a week

What to consider when writing a good survey

-Question structure (Open vs. forced choice)

-Wording of questions

-Question order

Participant issues

1. Shortcuts and biases

   1. Response sets

   2. Fence sitting

2. Social desirability

3. Limits of what can be self report

Response set

When participants give consistent responses across questions to save time, rather than accurately answering each question

Ways to reduce response set

Include reverse-wording

Ex.

In most ways my life is ideal

If I could live my life over, I would change almost everything

Fence sitting

Participants hesistate to choose extreme answers and always opt for neutral responses

How to combat fence sitting

Get rid of neutral option

Social desirability biases

Participants may respond in a way they think is socially desirable

Ex. Person who doesnt answer truthfully about smoking or sexual behaviors

Way to combat social desirability biases

-Decide ahead of time: if someone responds in the socially desirable way x amount of times they won’t be included in the analysis

-Implicit association tests (person doesn’t know they’re responding undesirably)

Limits to self report

-Can’t ask more than what someone could reasonably know

-We don’t always know why we think, feel, believe something

-False memories

Designing a questionnaire steps

1.Define the problem

2.Plan how it will be administered

3.Write the questionnaire

4.Desk check (face validity, make sure questions are good)

5.Pilot survey

Observational research

A researcher watches or monitors participants (people or animals) and systematically records their behavior

Naturalistic observation

“In the wild”

-Can give the most accurate measure of behavior

Disadvantage: May not giver the opportunity to observe relevant behavior

Ex. Trying to see the amount of yelling at a hockey match

Controlled observation

Observation in a controlled setting

Ex. Driving simulators

-Reduces variability

Ex. Too much noise, can’t hear what people are saying

Disadvantage: Less natural, people know they’re being observed

Participant Observation

Experimenter interacts with participants

Disadvantage: Participants know they’re being observed

Observer bias

Observers have inherent biases that can affect interpretation of data

Ex. If you hear a loud noise you might could that as yelling at hockey game

To avoid observer bias

-Multiple researchers

-Very specific codings

-Double blind

Observer effects

Participants change behavior to match observers’ expectations/behavior

Ex. “Clever Hans”

To avoid: Double blind

Reactivity

Participants may act differently if they know they are being observed

*Observer isn’t cuing a behavior, people are just acting differently because they know they’re being watched

Ways to combat reactivity

-Blend in by unobtrusively observing

-Wait until participants are used to being observed

-Use implicit measures of the behavior rather than directly observing behavior

Ex. Looking at cigarette butts

Self-report vs. observation

Self-report: Rely on participants reflecting on their thoughts, feelings, or behaviors

Observation: Records actual behavior. Some behaviors are hard to record with observation (ex. feelings of self-worth)

What type of claim do we typically test with correlations

a. Frequency

b. Association

c. Causal

b

What makes a study correlational

Only measured variables (no manipulated)

Sometimes thats all you can do

-Age

-Ethnicity

-Family status

-Brain injury

Do correlational studies have quantitative or qualitative variables

Quantitative, no nominal variables

Correlation statistic

Tells us about the link between values of two variables

• Strength

• Direction

-Range from -1 to 1

-Knowing the value of one variable tells us about the value of the other variable

Strength and direction

Strength: Can be visually estimated by how close the points are to a trendline. Range -1 to 1

Direction: (pos/neg) shown by the slope

little p

Population parameter for the statistic

Exists somewhere out there, we just don’t know it

Inferential statistic

little r

Correlation coefficient

The data we collect, organize, and summarize with descriptive statistics

How does the sample size affect the variation of sample estimates around the population estimate

it decreases because sample becomes closer to the real life number

r

-unitless measurement

-effect size for the strength of the relationship

-effect sizes are comparable across different variables and studies

-no matter what we’re measuring, r is on the same scale

Effect size

Effect size is a quantitative measure of the magnitude or strength of a relationship or difference, independent of sample size

More extreme vlaue = more extreme relationship = bigger effect

Null hypothesis

Default: There is no relationship H: p > 0

Alternative HA: p < 0

Computing r

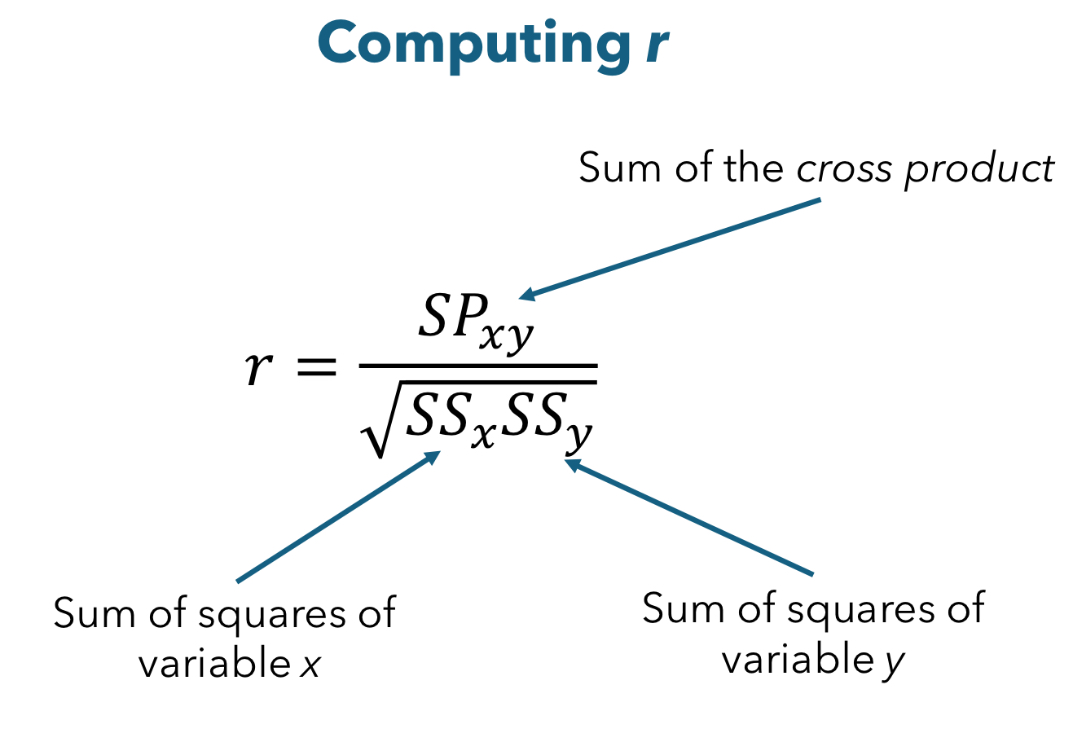
Denominator

Sums of squares for x times sums of squares for y

Square rooted

Tells us about the variability of the two variables

Sums of squares

(X_i-mean)² + (Y_i-mean)²

Numerator

How much variability is related between those two variables

SP_xy

((X_i-mean) times (Y_i-mean))

What does it mean if r=1 or r=-1

All variability is shared

Perfectly moving together in a pos/neg way

What part of the r equation can be negative

Numerator

Denominator has sums of squares where things are squared

Strength of correlations

Strong: (0.7,1]

Moderate: [0.5,0.7)

Weak: [0.3,0.5)

None or very weak: [0, 0.3)

Outliers impact on correlation

Impacts correlation

Possibilities:

1. Outlier above the line - when this happens relationship is strengthened

2. Outlier below the line - when this happens the relationship is either weakened or will mask it

Sample size impact on correlation

Increased sample size = increased power

If power is high then we can call it stat. sign more easily

Doesn’t matter as much for stronger correlations but does for weaker ones

Effect size vs. Statistical significance

Effect size = strength

Stat. sign = the p-value

P-value is determined by effect size and sample size:

• Larger the effect size, lower the p-value

• Larger the sample size, lower the p-value

Range restrictions

Correlations may exist across a wide range, but be imperceptible in small portions of the range

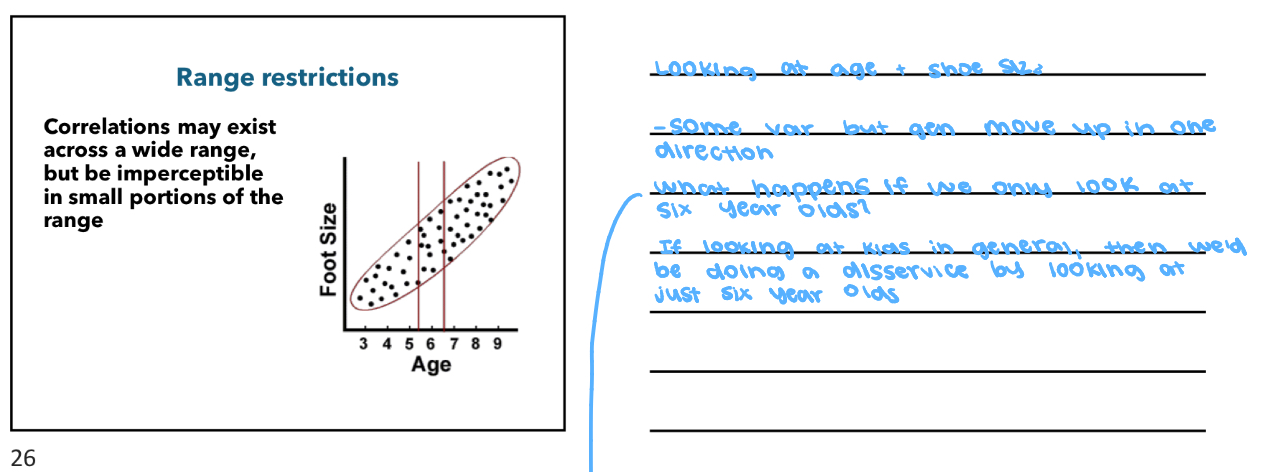
If we just look at one portion, then the relationship changes

-Range restrictions often arise from biased sampling

Third variables

When a relationship arises because of another variable

Ex. Grip strength and Memory

Third variable: Age

Ex. Height and reading score

Third variable: Grade level

Problem of establishing causation

1. Covariance

2. Temporal precedence

3. Internal validitity

Covariance

How much two variables change together

-In other words: is there a correlation

-Scores being related to each other is necessary for establishing causation, but not sufficient for establishing causation

-This is why correlation does not always mean causation

Temporal precedence

Ability to know which variable comes first

Ex.

Teachers niceness > Student learning

Student learning > Teachers niceness

Internal validity

The extent to which the effect arises because of variable(s) of interest, and not some alternative variablesM

Reporting statistics in APA style

Symbols are italicized but the values are not

M = 3.25 (SD = 1.10)

r = .57, p < .05

For most results, round 2 decimal places, for p-values round 3

For correlational need to have degrees of freedom and either p-value or CI

Don’t use a leading zero (Ex. 0.30) (Correct: .30)

Regression Equation

Describes the precise numeric relationship between the variables

Best-fitting line

Lets us predict scores of one variable given scores of the other in measured units

Regression line = Best-fitting line

Lets us go beyond strength of relationship and let us predict future data points

Homoscedasticity

Assumption that error in our prediction is evenly distributed across range of x and y

Least-squares method

Minimizes errors in prediction based on our regression line

Error = Y-Y_predicted

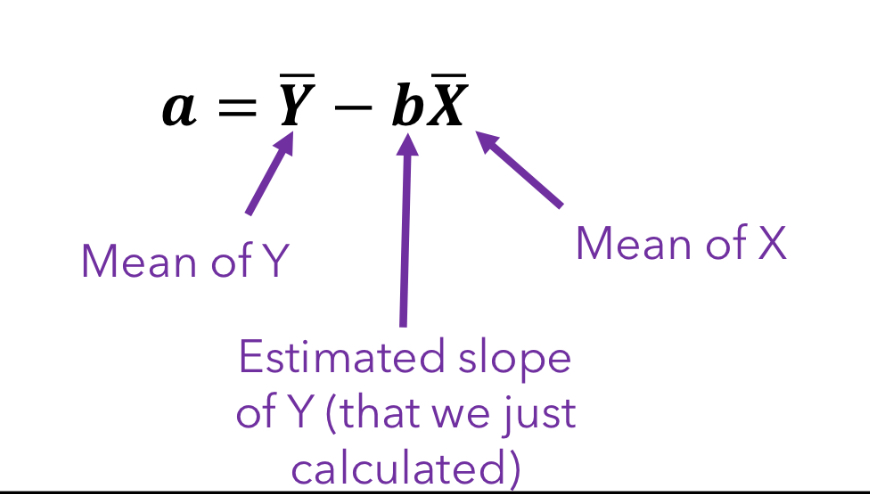
Least-squares regression equation

Y_i’ = bx_i + a

Y_i’ = Predicted value of y_i

b = Estimated slope of Y (b) times value of x_i (our x score of interest)

a = Estimated intercept

Regression line example

How many behavioral problems per class period could we expect if we give students 30 minutes of recess?

How do we compute b?

(b = the slope of the line)

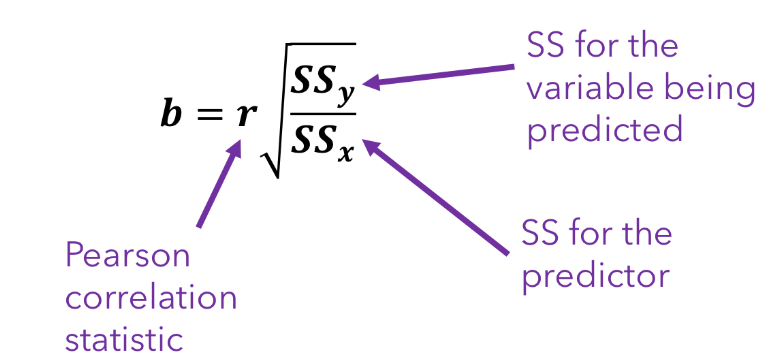
How do we compute a?

(a = the intercept of Y)

What do you calculate first in the regression formula

b (slope)

Regression lines let us predict Y scores from X scores

True

False

True

Standard error of the estimate

Amount of deviations from the predicted line in units of the predicted variable

SD = Average dev’s from a mean

SE = From the reg line

Standard error formula

If you have a SE of three what is that telling you

In general, the prediction from the regression line is off by three points

If exam question was “which of these SE would you want to have” choose the lowest one

The units are in the OG

What does the standard of the error represent

The amount of unexplained variability

The standard error of the estimate tells you how far off the model’s predictions typically are from the actual values.

r squared answers what

How good we are at capturing the variability

How much variability in Y the regression explains with X

How much better we did by using X instead of simply the mean of Y

Proportion of variability

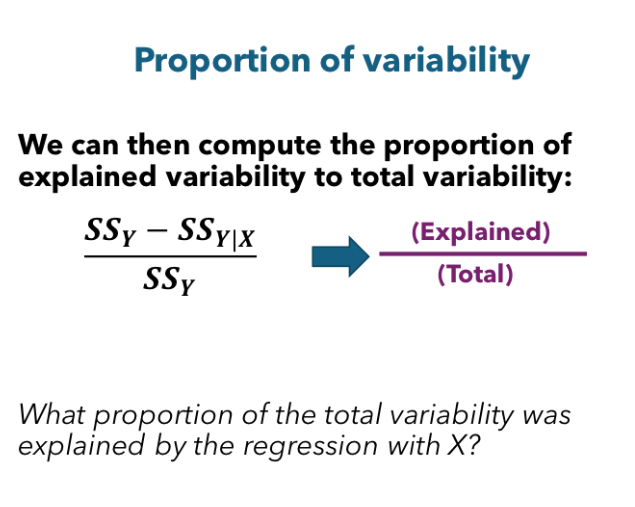
This proportion is known as r²

r²

The proportion of total variability in one variable that is predictable from another

r²= 0

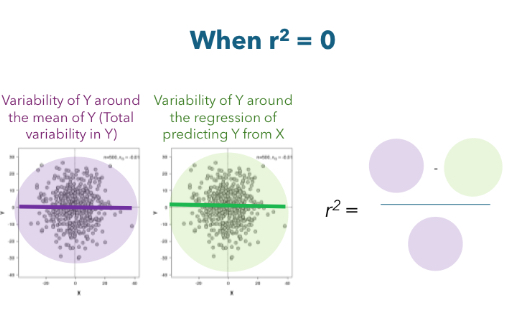
We would be just as accurate by predicting Y from the mean of Y than by using X to predict Y

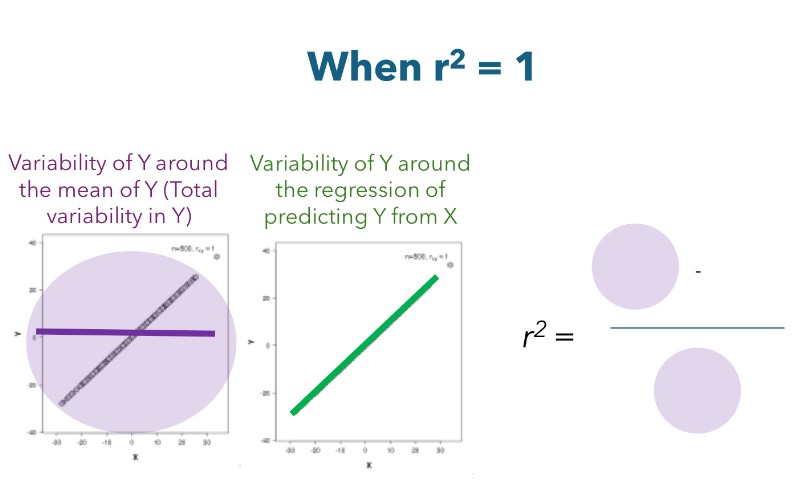
r² = 1

Multivariate regression

-Two or more predictor variables

-One dependent variable

Ex. Want to predict income:

-Might want to study years in the workforce

-Education

Standardized beta

Change in the dependent variable, in standard deviations, per standard deviation change in the predictor

Ex.

Unstandardized beta (B = 0.0351)

Change in likes for one follower

Standardized beta (β = 0.410)

Change in likes for one SD of followers

Limits to regression approach

-Do not establish temporal precedence

-Can only control for what they measure

Can’t be sure all third variables are accounted for

Third variable

A variable that represents a plausible alternative explanation for an existing correlation between two variables

-May imply the existing correlation is meaningless because the two variables are not directly related

Ex. Grip strength and memory. Third variable: age

Mediator

A variable that helps explain the meaningful association between two variables that have an existing correlation, because the variable arises from or is internal to the independent variable

Ex. Minutes of recess and behavior problems in the classroom

Third variable: inhibition skills

Moderator

When the relationship between two variables changes in strength depending on the level of a third variable

Moderator modifies the strength or direction of the association

Ex. Recess and behavior problems

Moderator: Physical activity

Four validities

1. construct - how well the variables in a study measure what they are intended to measure. Exhaustive and selective

2. external - The degree to which the results of a study are generalizable to a larger population

3. internal - The degree to which the effect arises because of the experimental variable and not some alternative variable

4. statistical - The degree to which the results support the claim