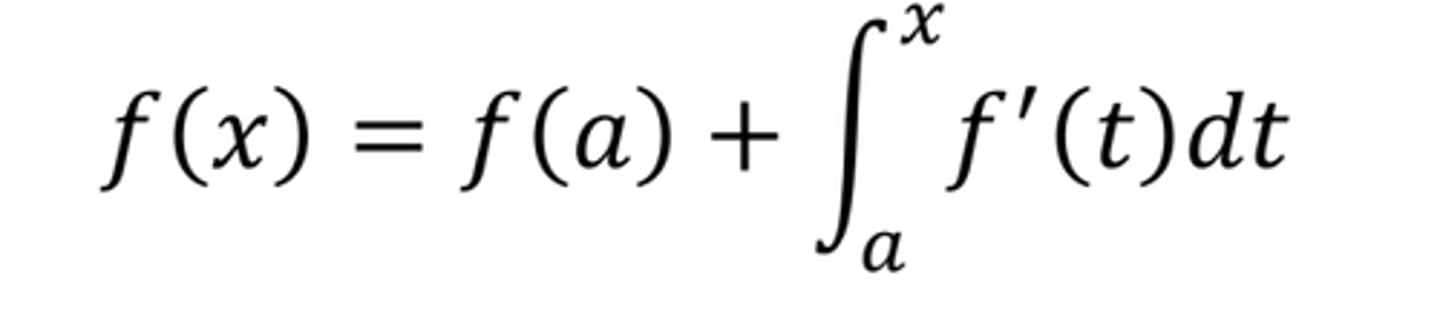Calc AB Formulas

d/dx (c)

0

d/dx (xⁿ)

nxⁿ⁻¹

d/dx (cxⁿ)

cnxⁿ⁻¹

d/dx (u(x)+v(x))

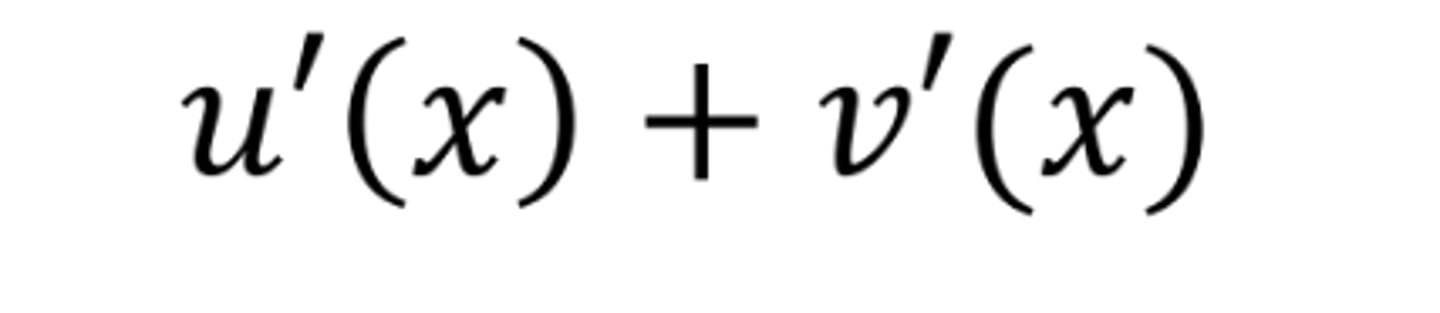
d/dx f(g(x)

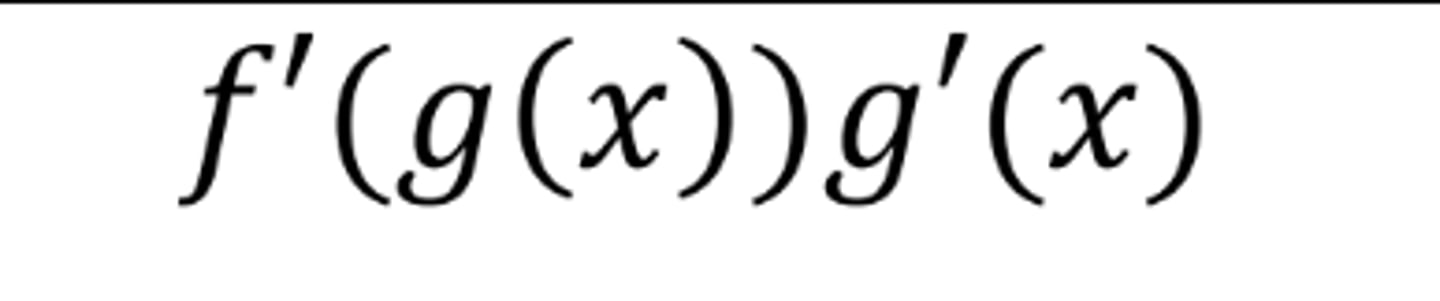
d/dx (f(x)g(x))

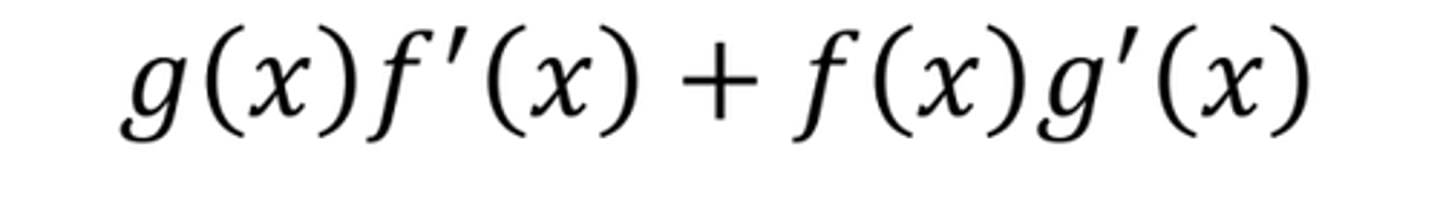
d/dx (f(x)/g(x))

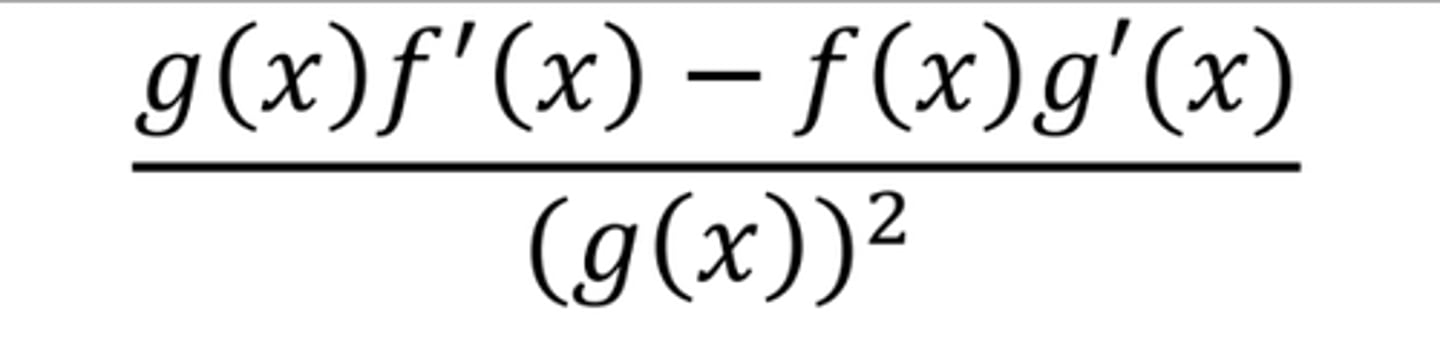
d/dx sin(x)

cos(x)

d/dx cos(x)

-sin(x)

d/dx tan(x)

sec²(x)

d/dx sec(x)

sec(x)tan(x)

d/dx csc(x)

-csc(x)cot(x)

d/dx cot(x)

-csc²(x)

d/dx eⁿ

eⁿ

d/dx aⁿ

aⁿ ln(a)

d/dx ln(x)

1/x

d/dx logₙ(x)

1/(x)ln(n)

d/dx f⁻¹(x)

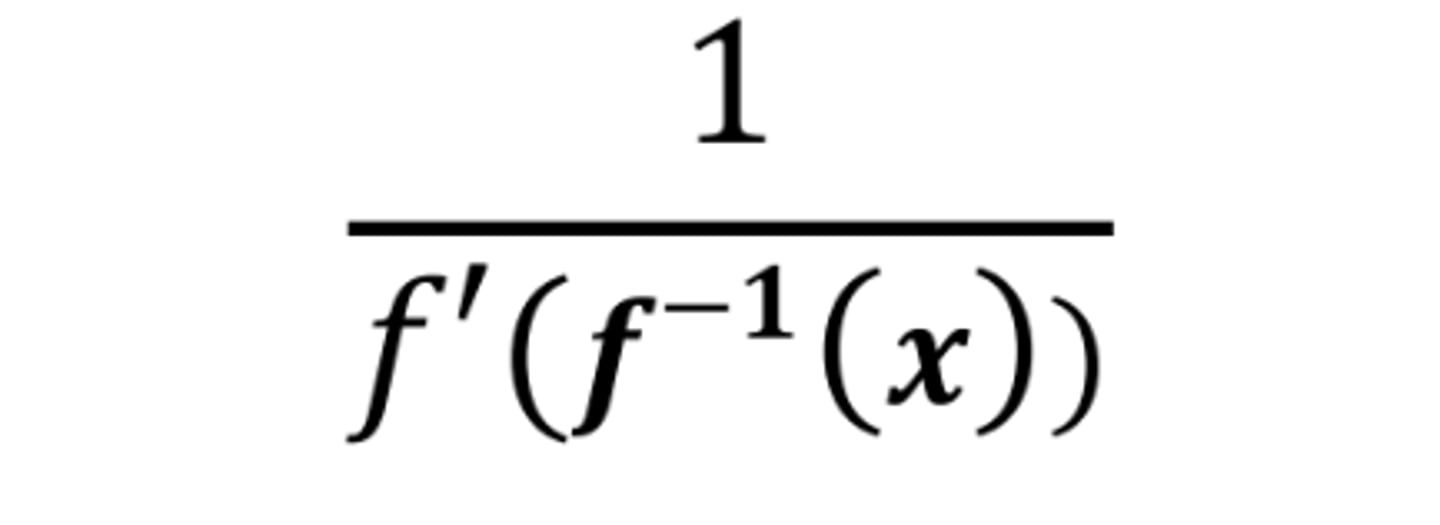
d/dx arcsin(x)

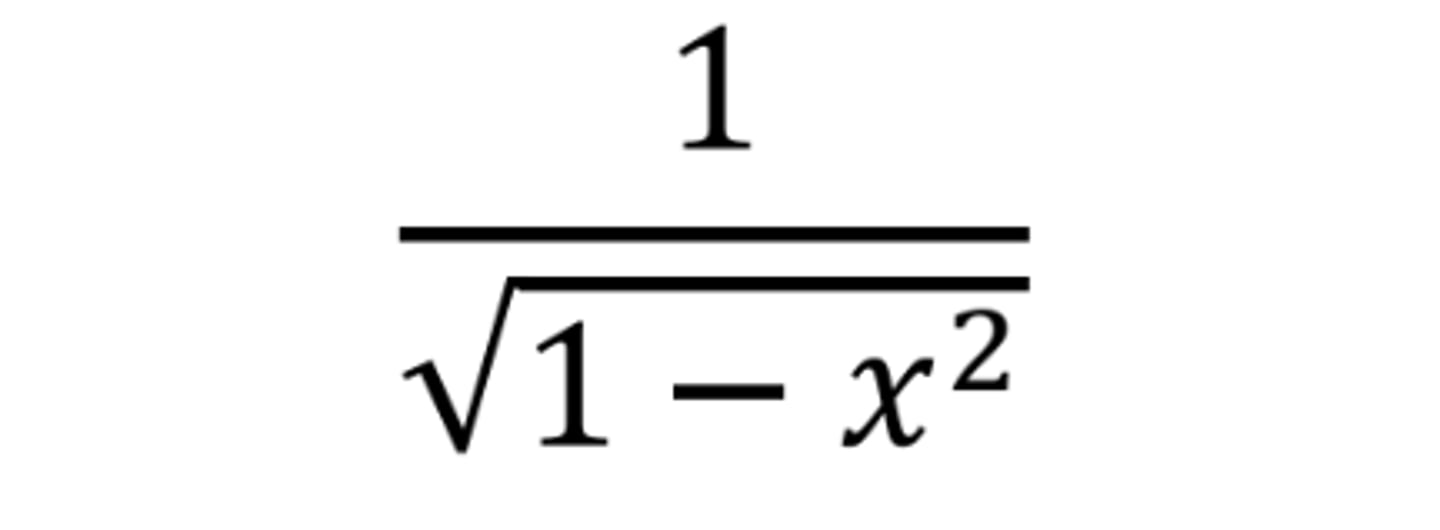
d/dx arccos(x)

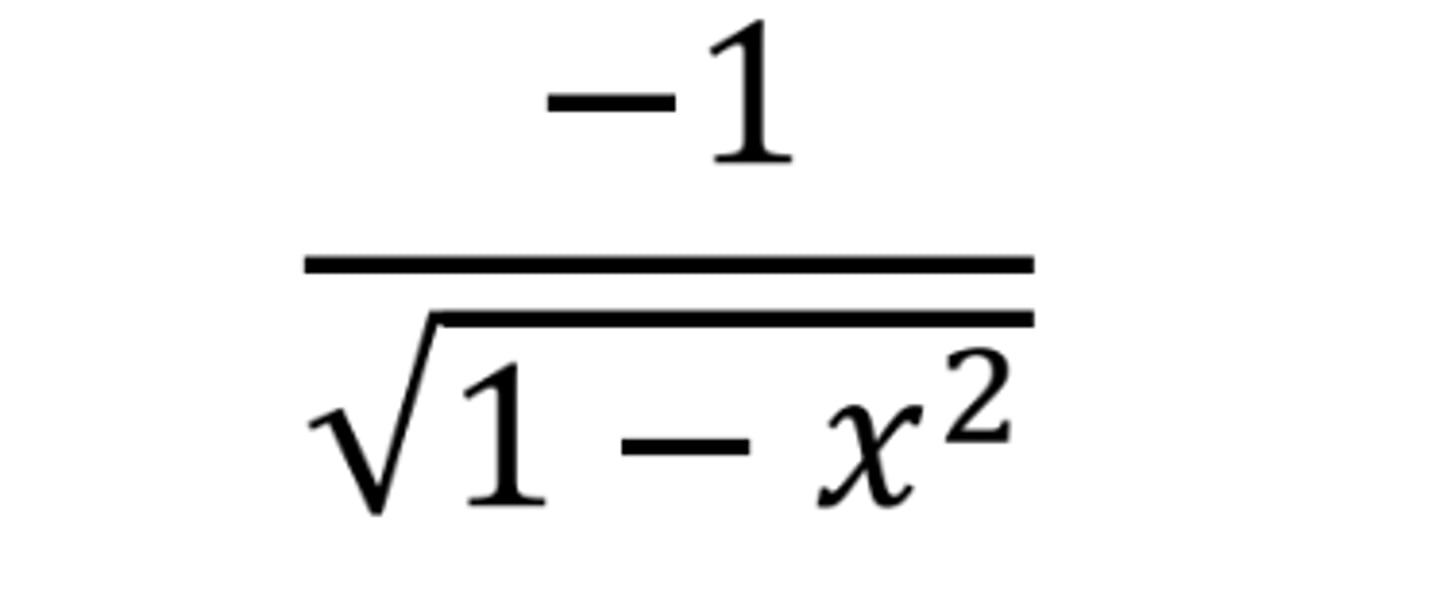
d/dx arctan(x)

d/dx arccsc(x)

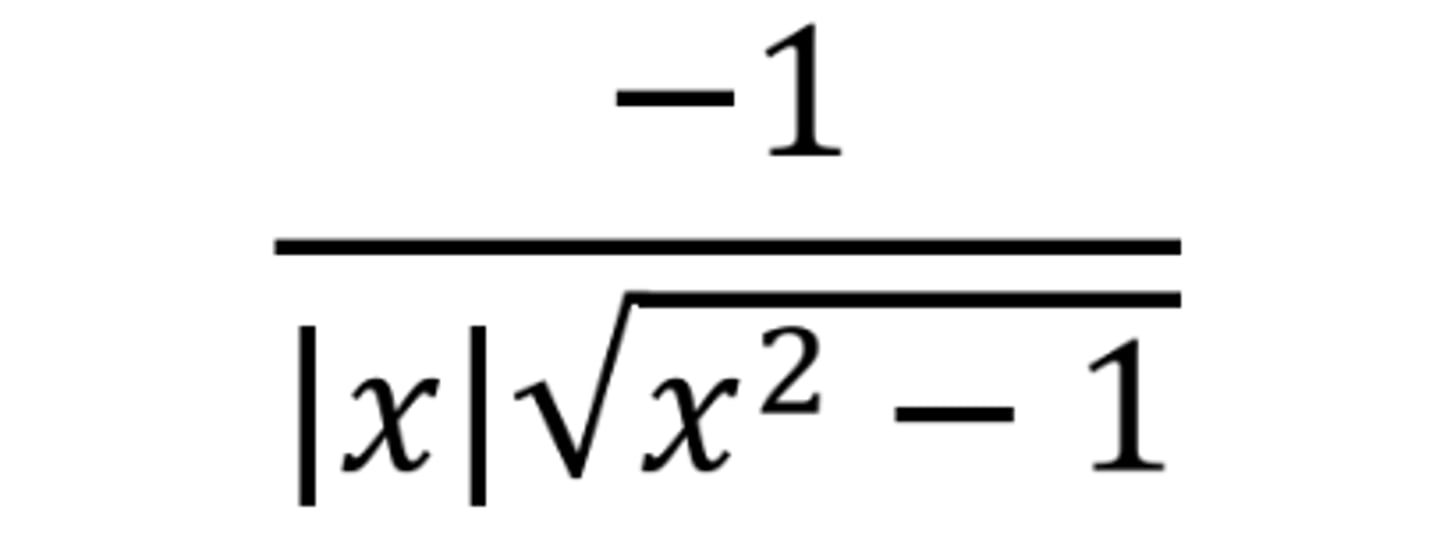
d/dx arcsec(x)

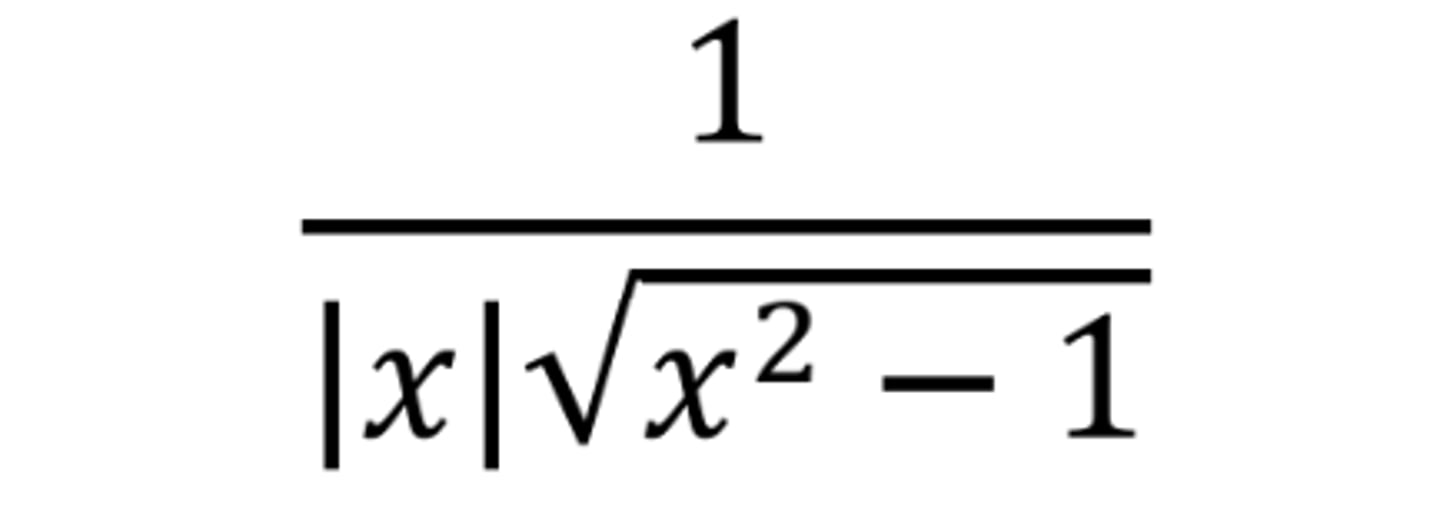
d/dx arccot(x)

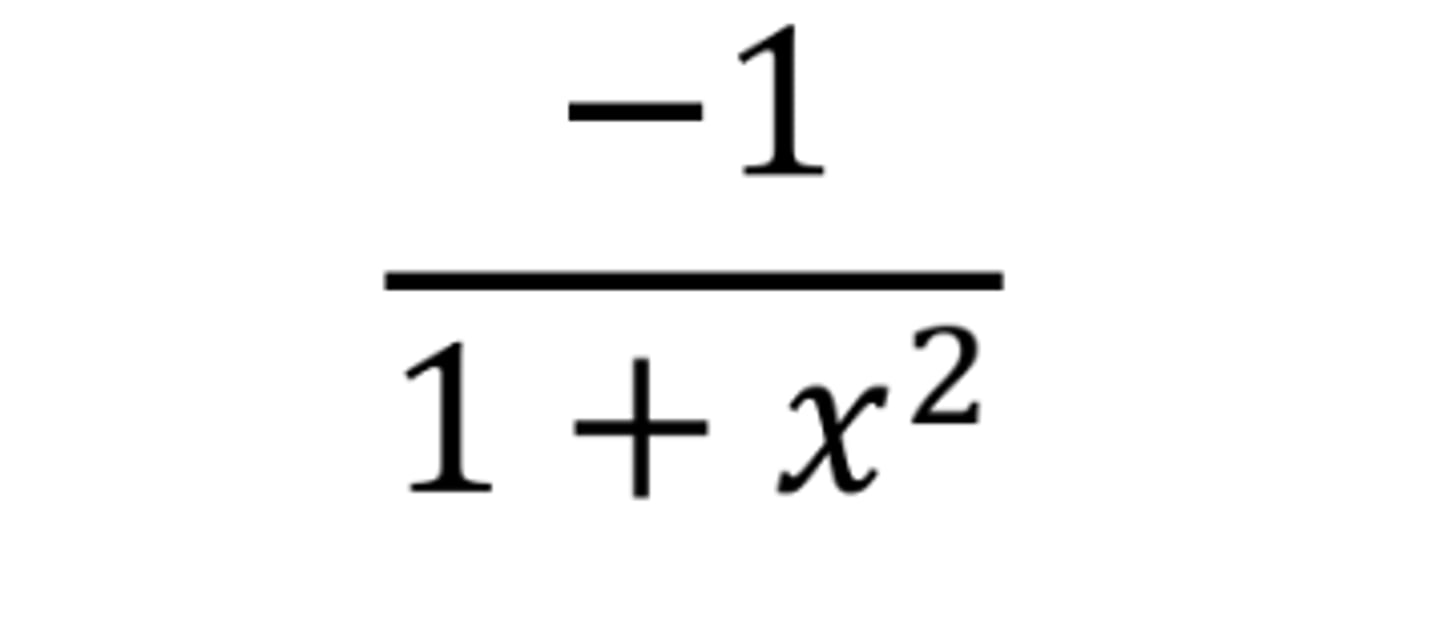
Intermediate Value Theorem

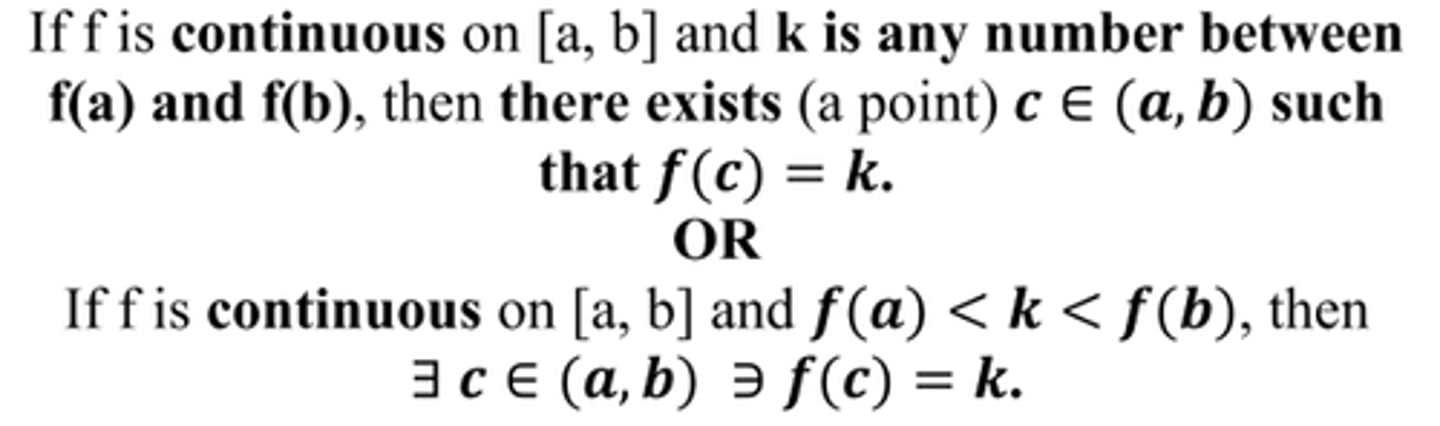
A function f is continuous at x=a if the following conditions are satisfied:

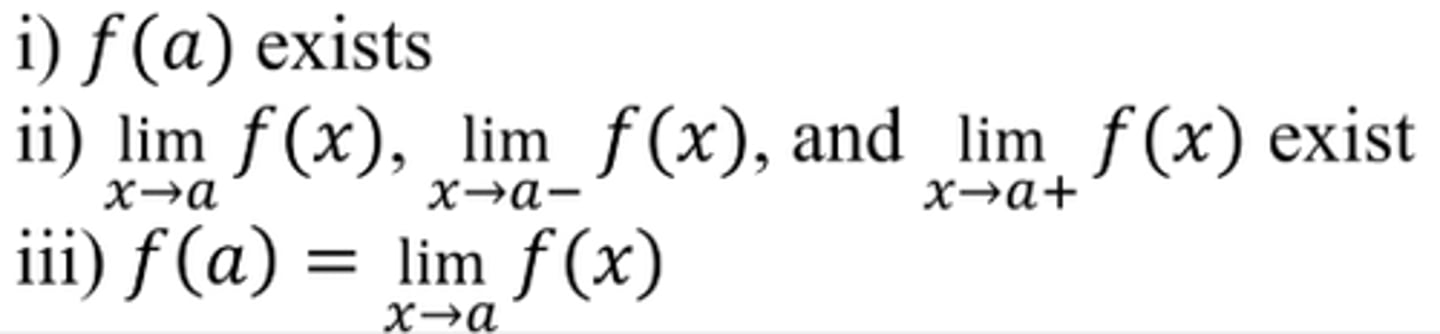
Limit Definition of a Derivative

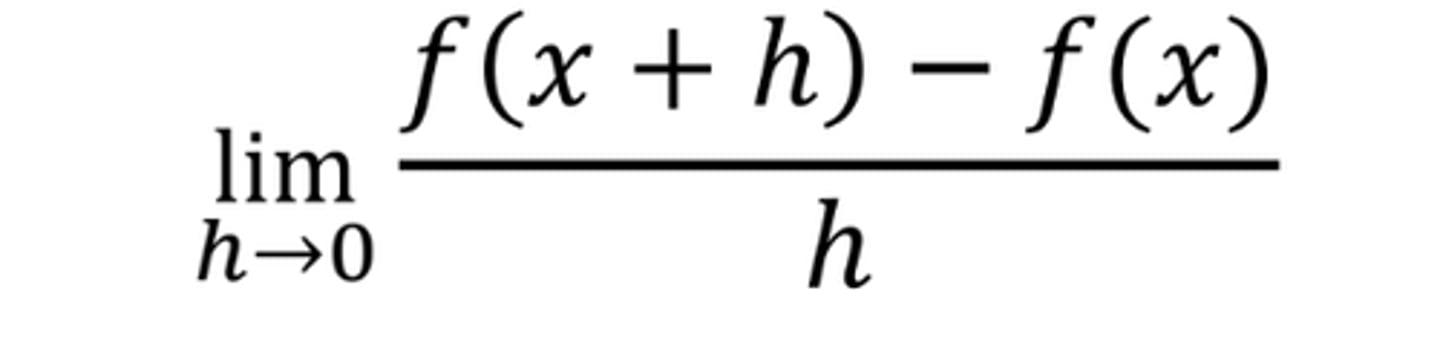
Alternate Form of the Derivative at x=c

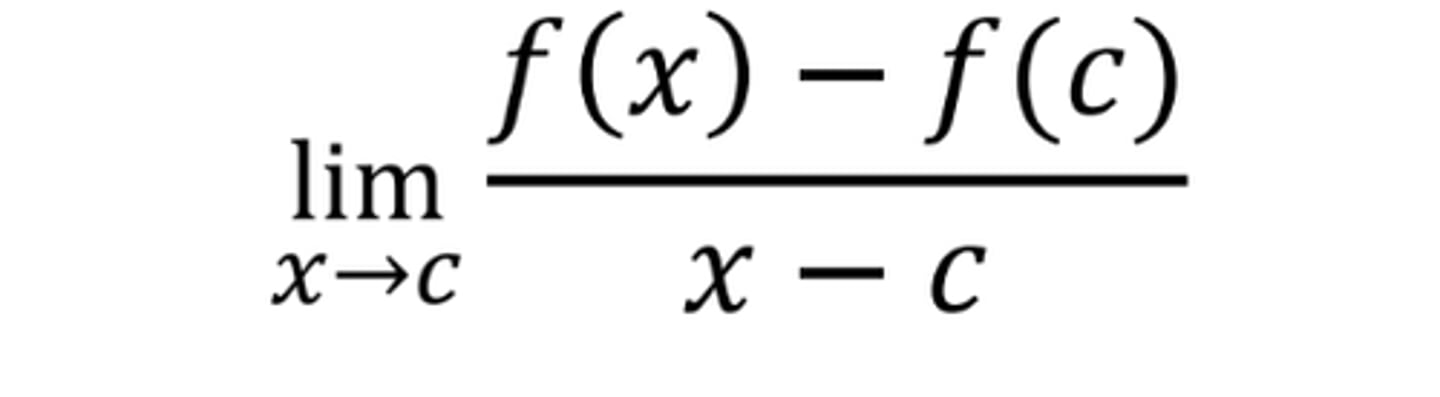
Average Rate of Change of f(x) on [a, b]

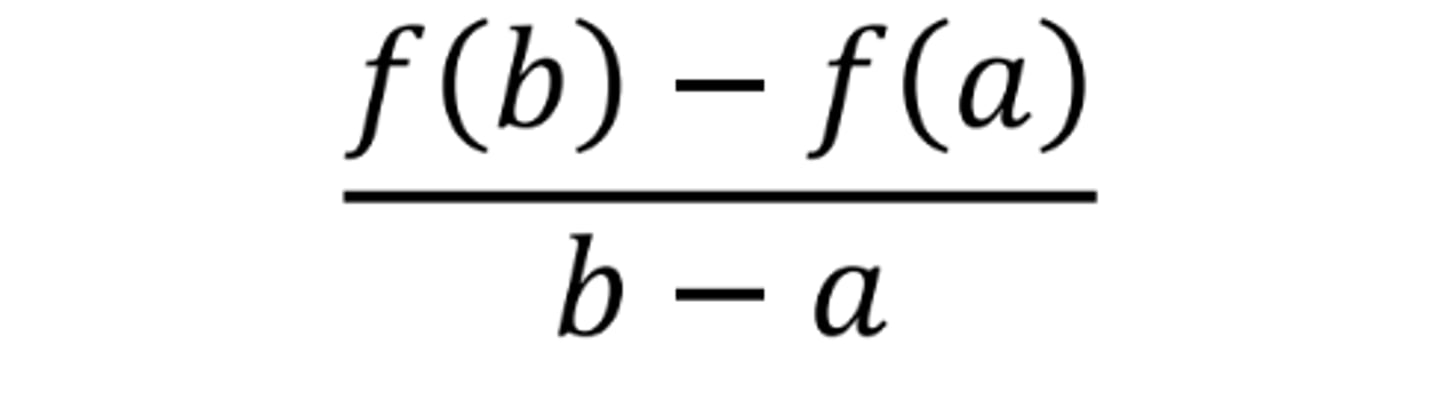
sin²(x)

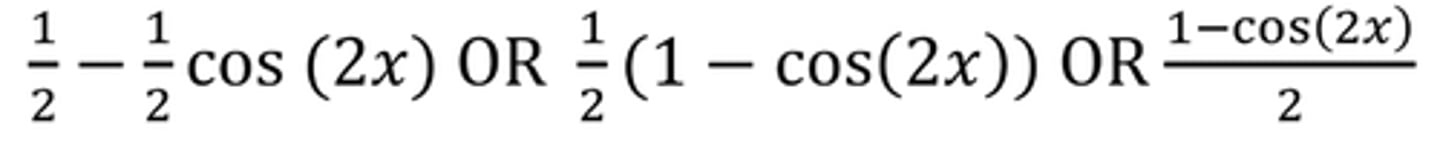
cos²(x)

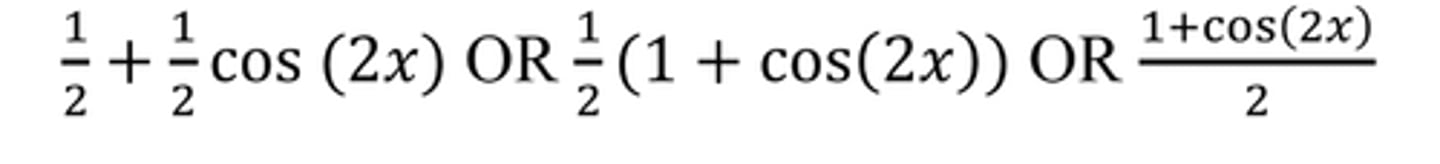
sin(2x)

2sin(x)cos(x)

cos(2x)

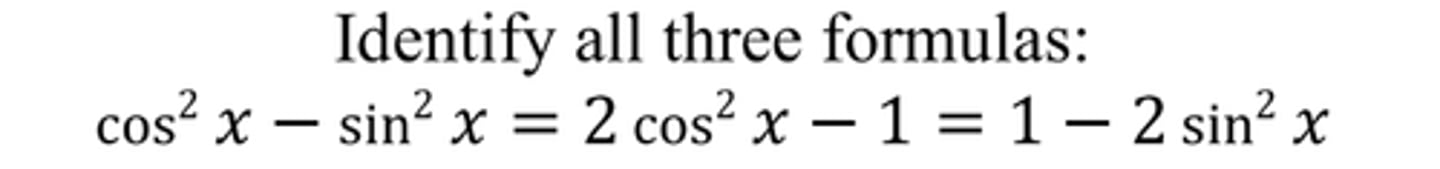
Pythagorean Identity

sin²(x) + cos²(x) = 1

Area of a Circle

A = πr²

Circumference of a Circle

C = 2πr

Volume of a Prism

V = Bh

(where B = area of the base)

Volume of a Right Circular Cone

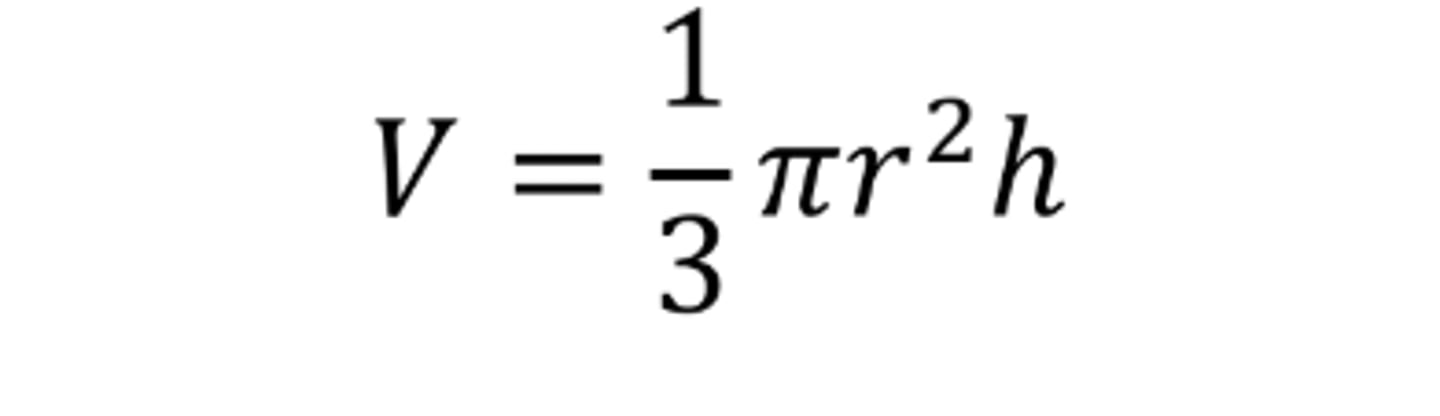
Volume of a Sphere

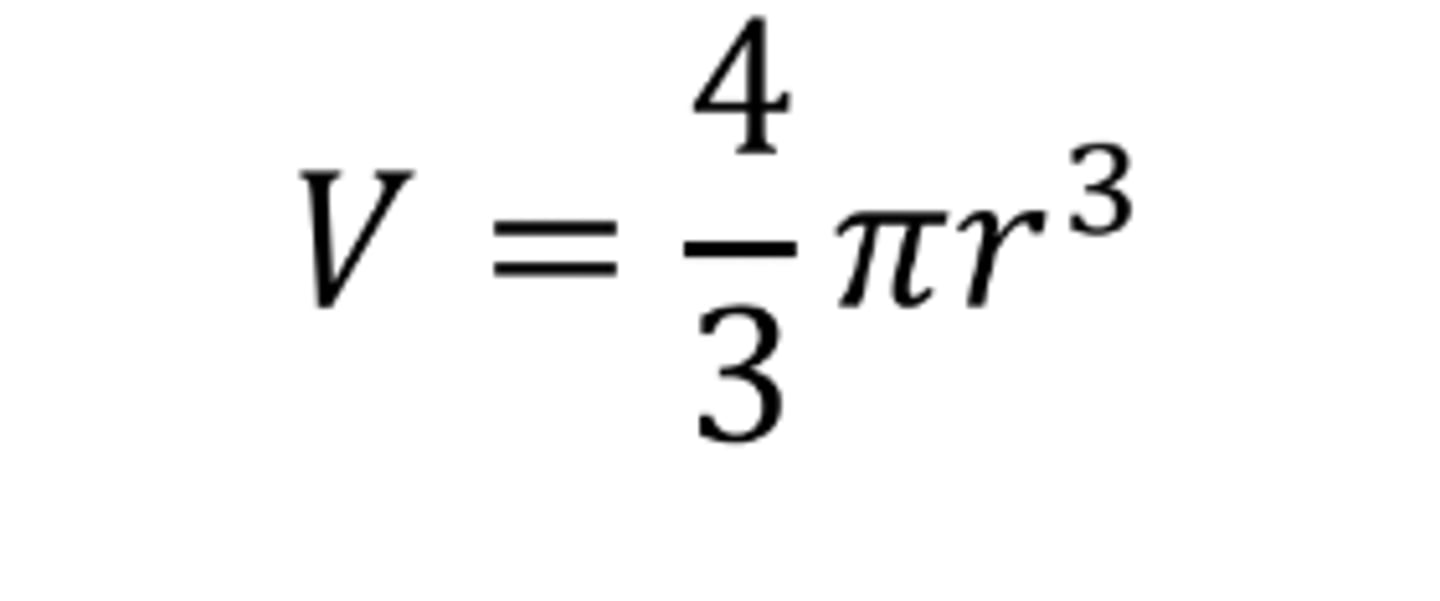
Volume of a Right Circular Cylinder

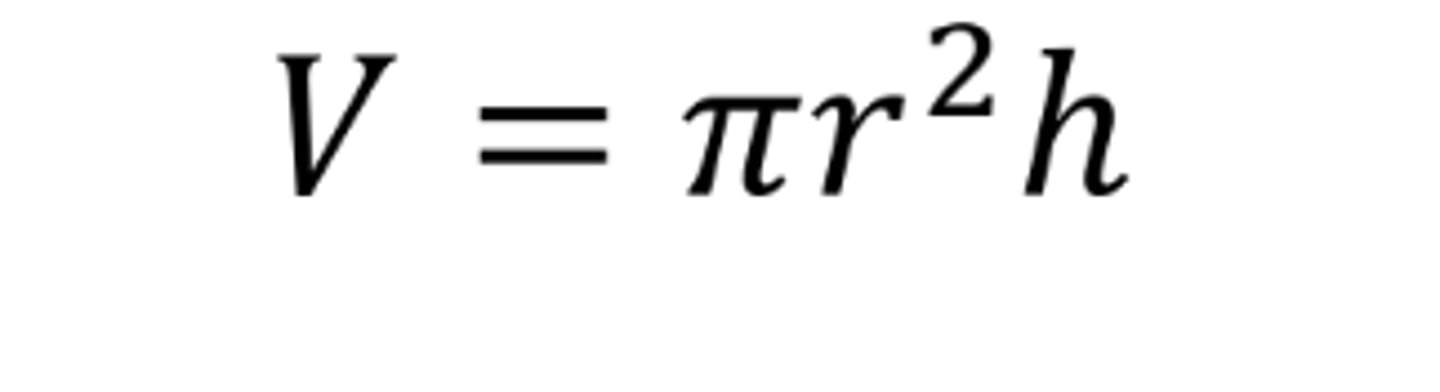
Surface Area of a Cylinder

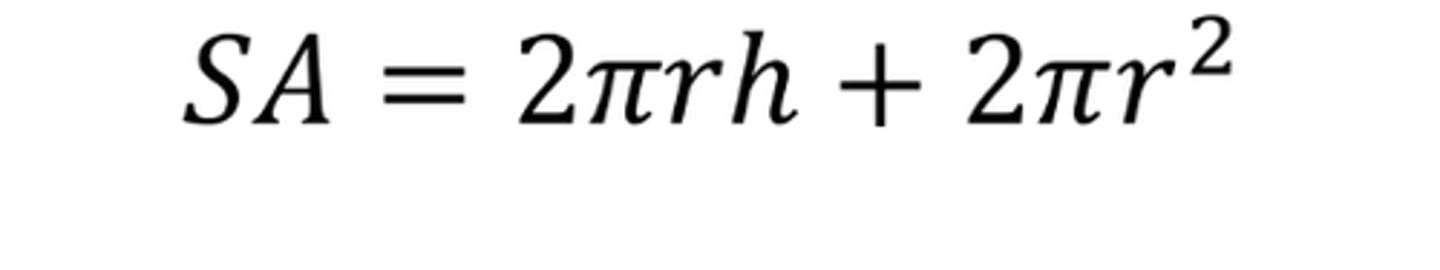
Volume of a Cube with side s

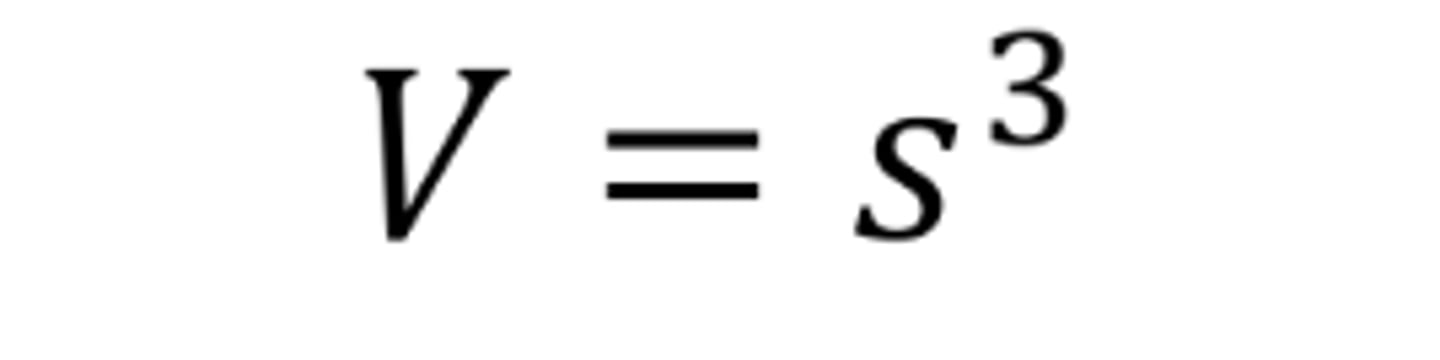
Area of a Non-Right Triangle: lengths a & b and angle C

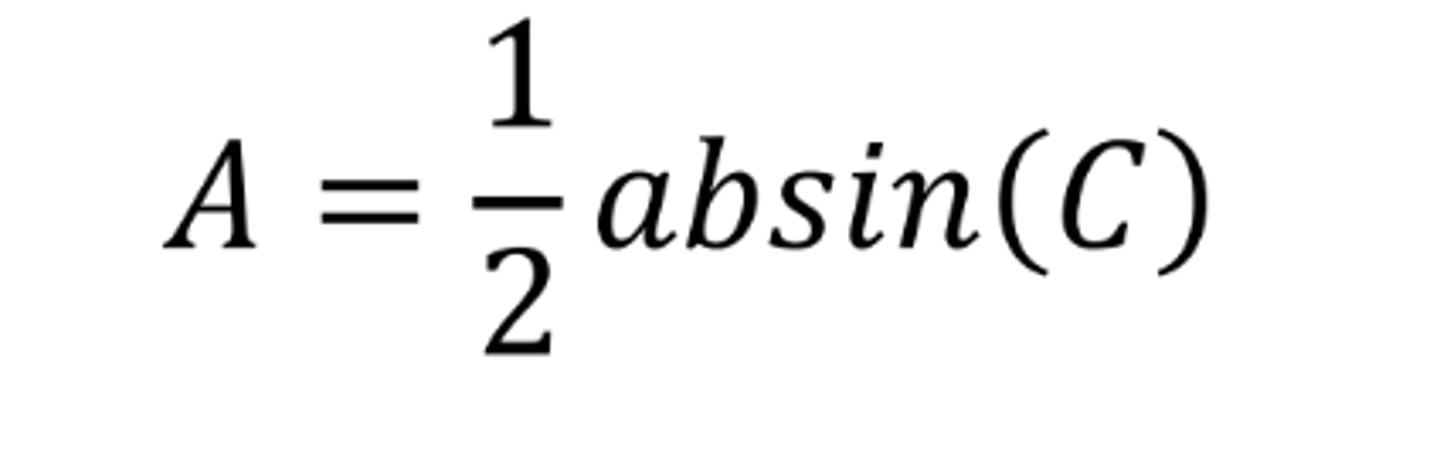
Rolle's Theorem

Mean Value Theorem

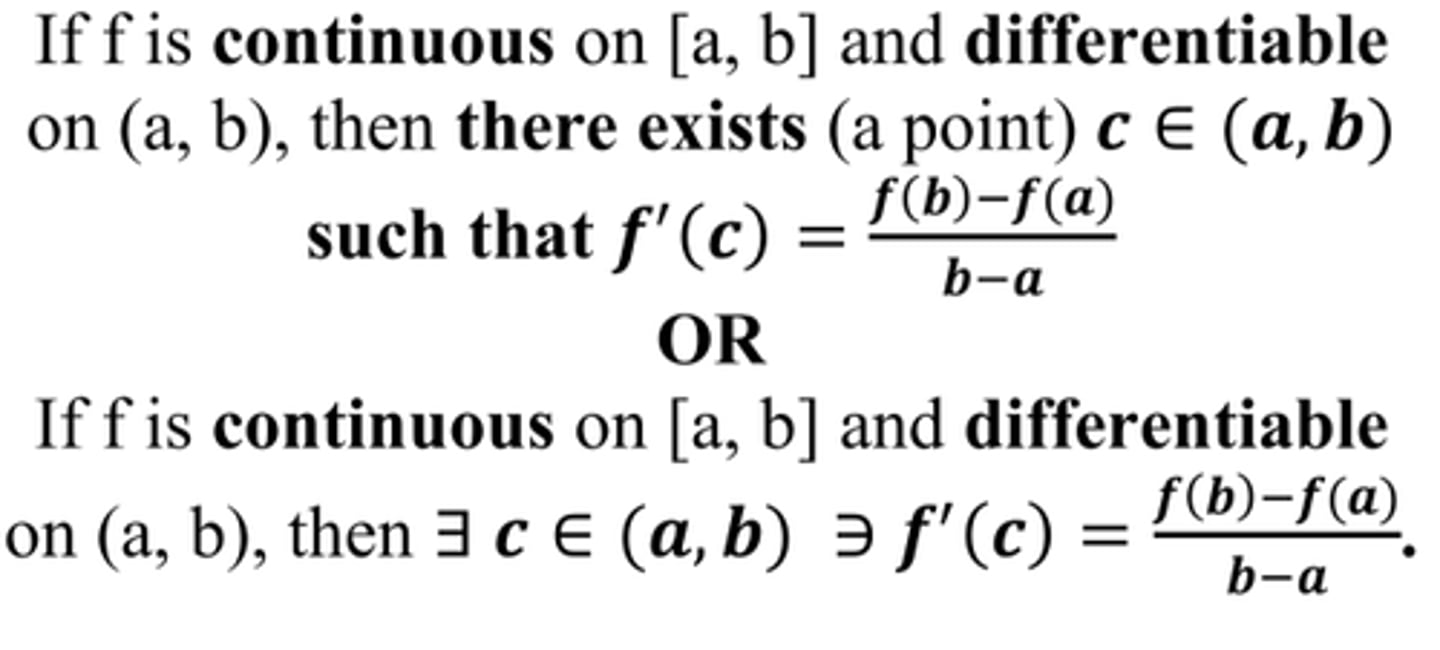
Extreme Value Theorem

∫xⁿ dx

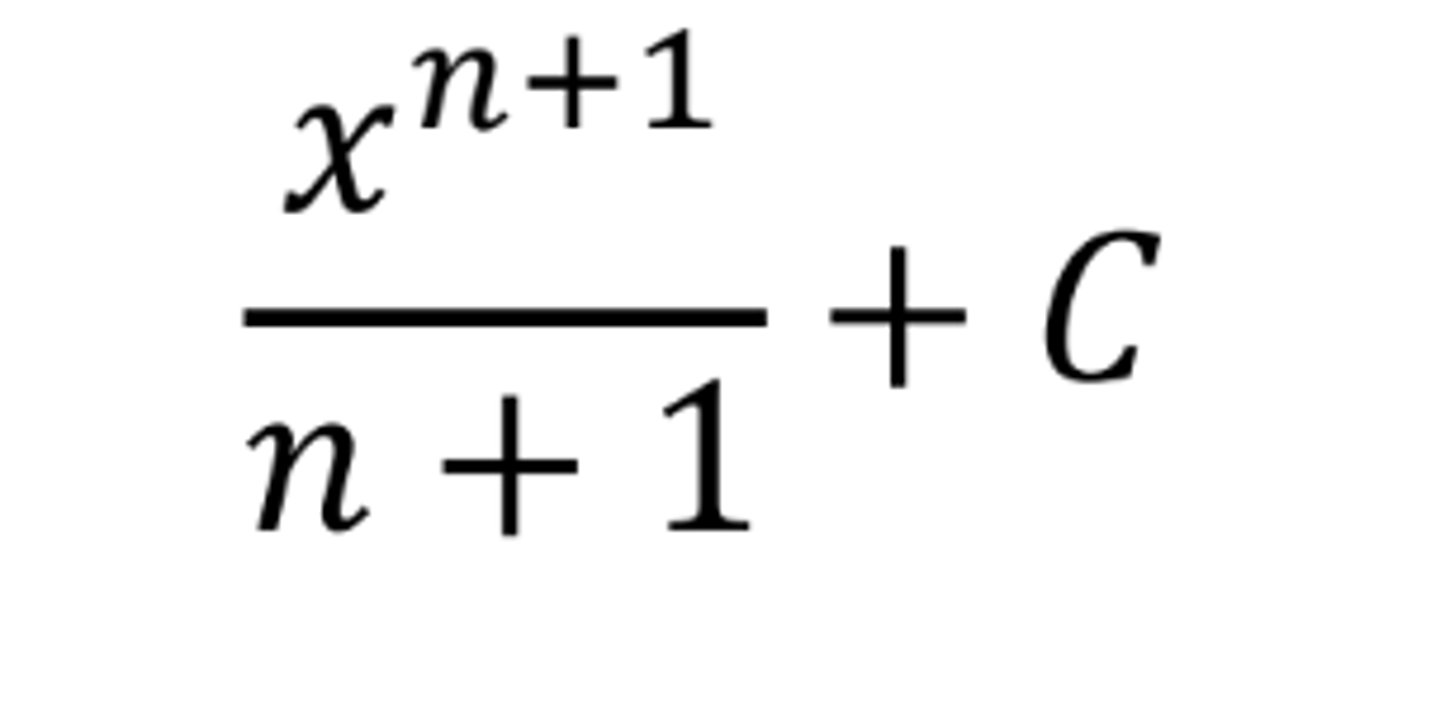
∫1/x dx

ln|x| + C

∫sin(x) dx

−cos(x) + C

∫cos(x) dx

sin(x) + C

∫eⁿ dx

eⁿ + C

∫aⁿ dx

aⁿ/ln(a) + C

∫tan(x) dx

ln|sec(x)|+C or -ln|cos(x)|+C

∫cot(x) dx

ln|sin(x)| + C

∫sec(x) dx

ln|sec(x) + tan(x)| + C

∫csc(x) dx

-ln|csc(x) + cot(x)| + C

∫sec²(x) dx

tan(x) + C

∫sec(x)tan(x) dx

sec(x) + C

∫csc²(x) dx

-cot(x) + C

∫csc(x)cot(x) dx

-csc(x) + C

∫tan²(x) dx

tan(x) - x + C

∫1/√(a²+x²) dx

arcsin(x/a) + C

∫1/(a²+x²) dx

(1/a)arctan(x/a) + C

∫1/x√(x²-a²) dx

(1/a)arcsec(x/a) + C

Area of a Trapezoid where b = base & h = height

A = (½)(b₁+b₂)h

Definition of a Definite Integral using Riemann Sums (Define ∆x & xκ)

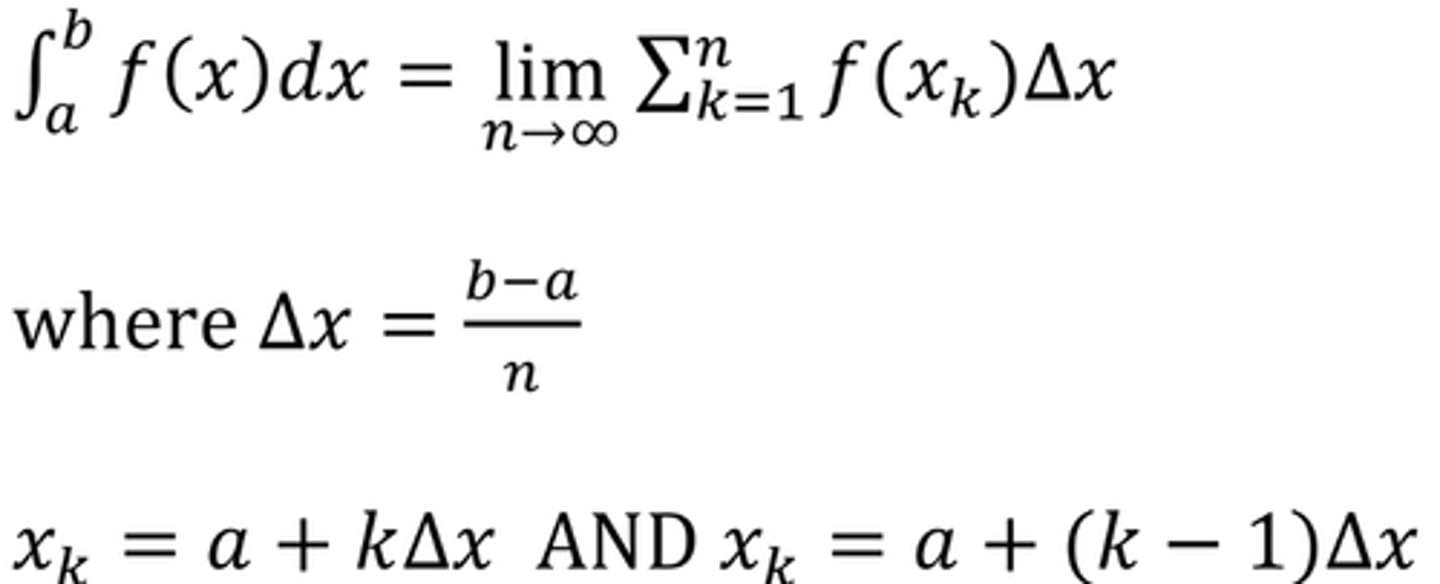
Fundamental Theorem of Calculus using an Integral of a Derivative

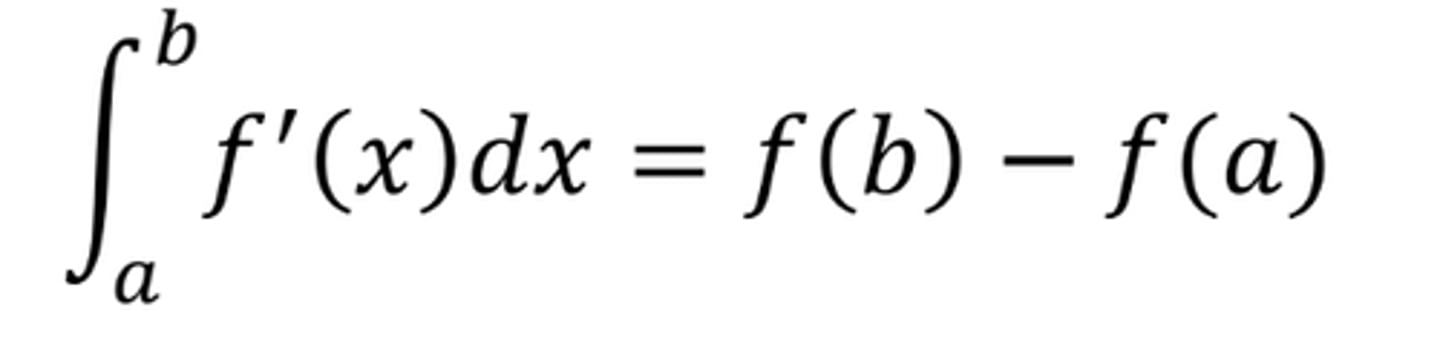
Average Value Theorem

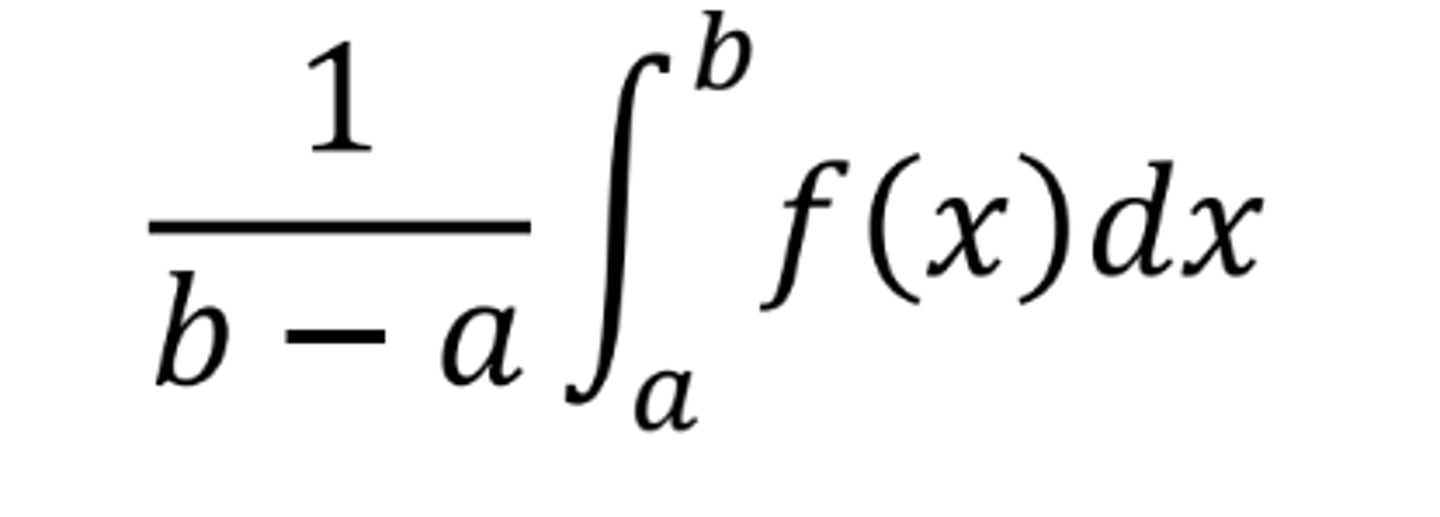
Area between two curves

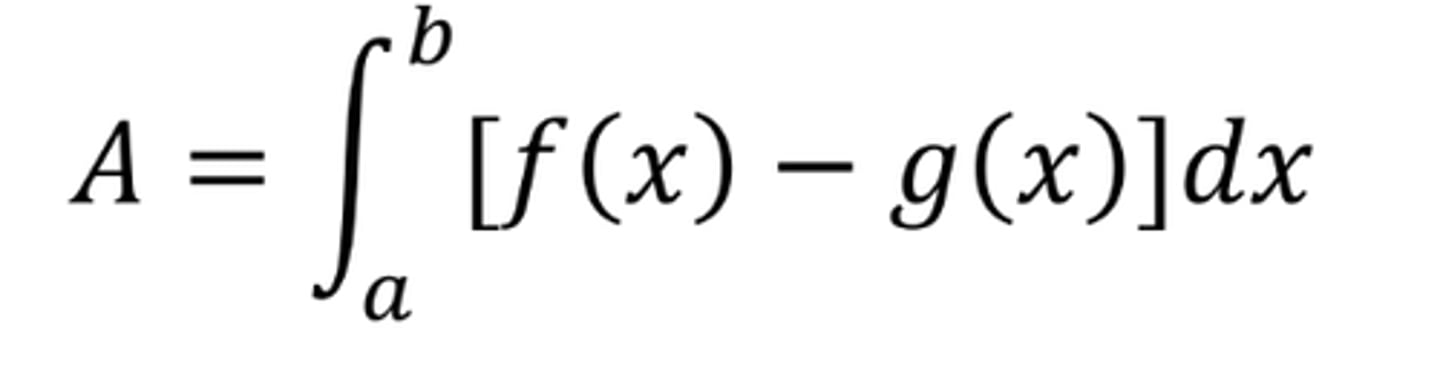
Volume by disk method (rotated around x-axis)

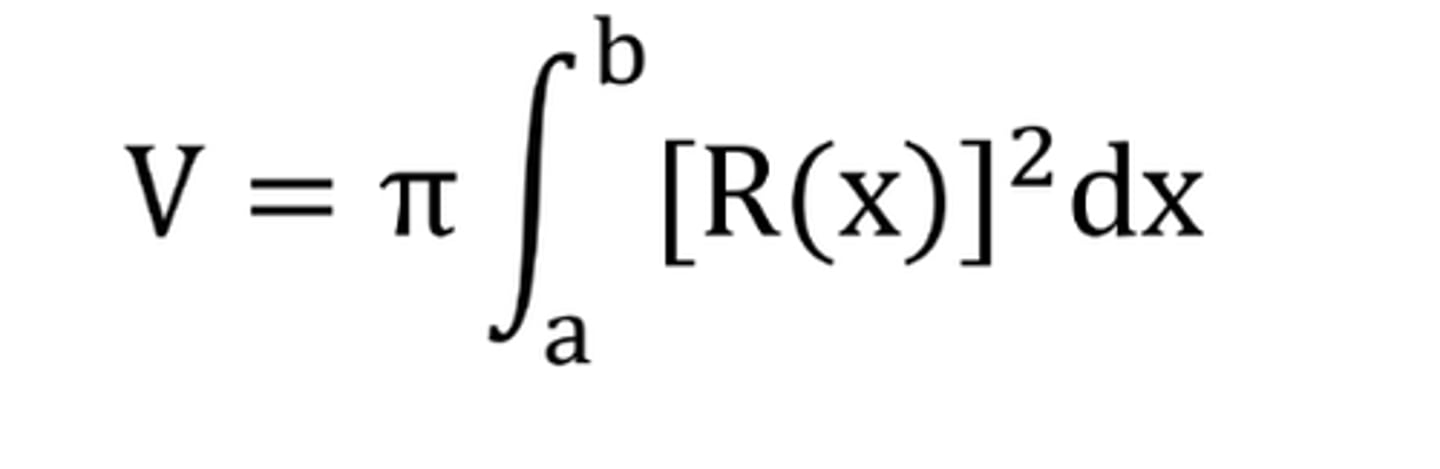
Volume by disk method (rotated around y-axis)

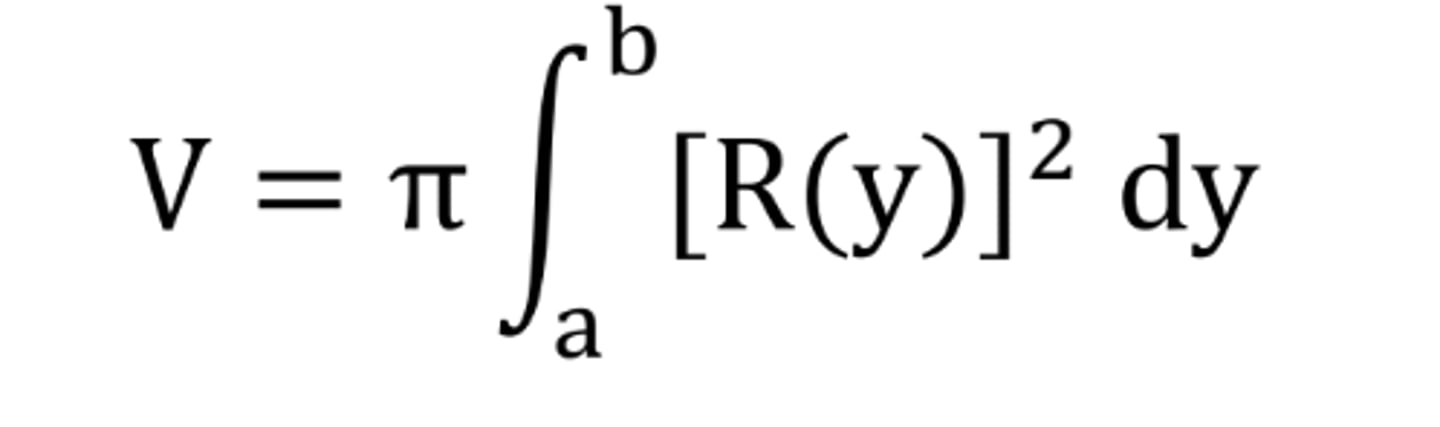
Volume by washer method (rotated around x-axis)

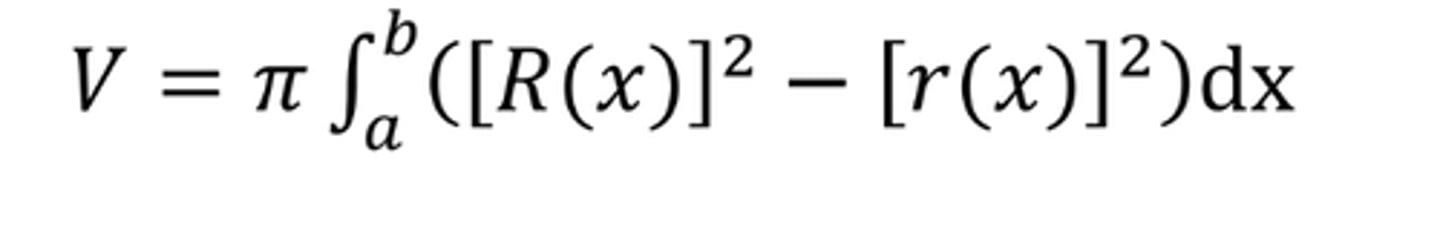
Volume formula using areas with known cross-sections in terms of x

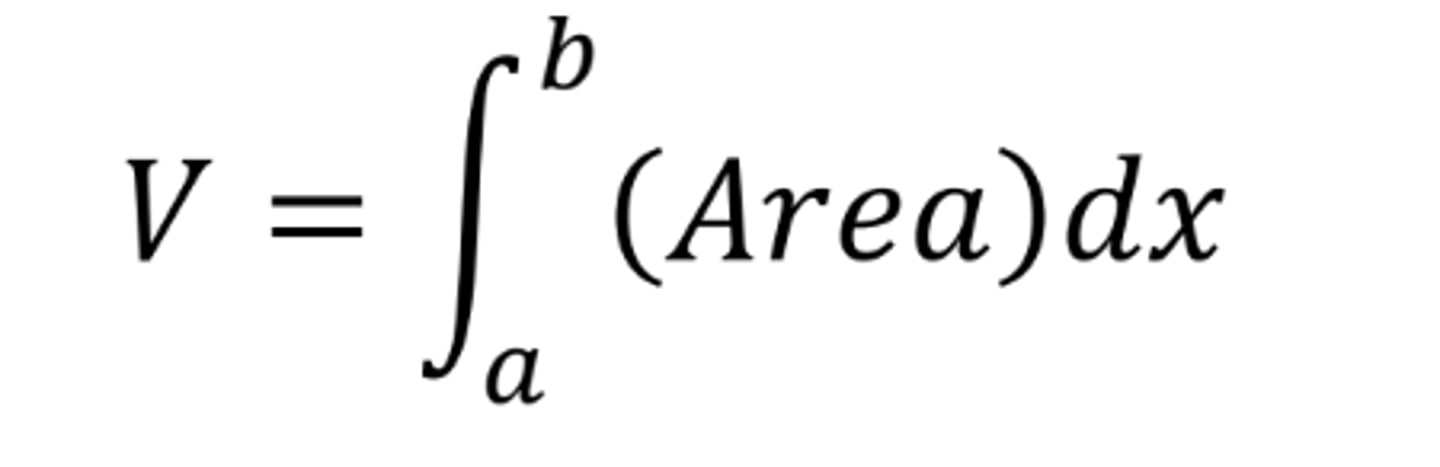
Area of a square with b as base

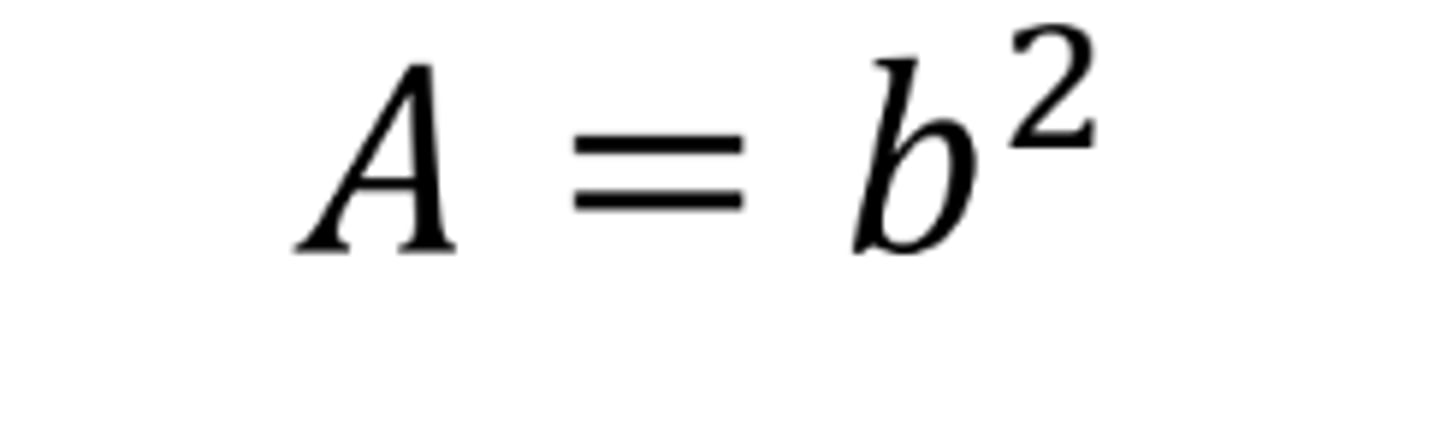
Area of a semicircle with b as base

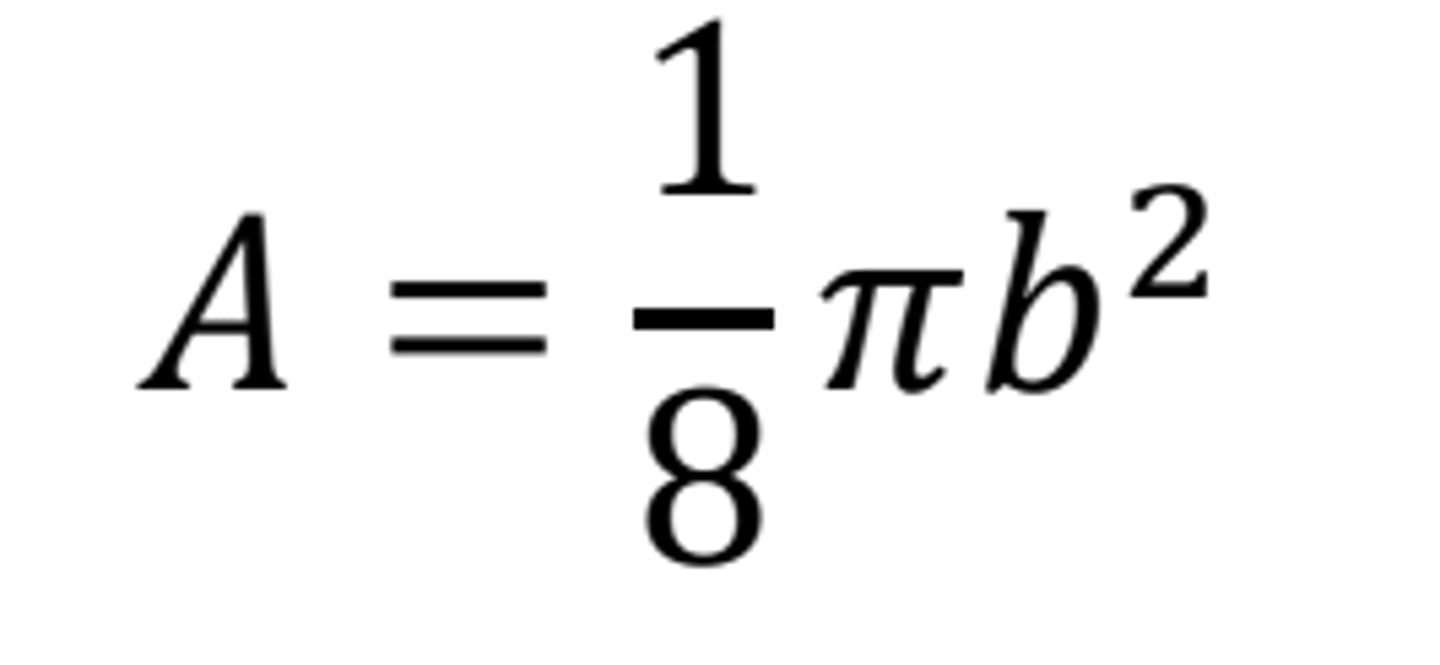
Area of a rectangle with h = ½b

Area of Isosceles right triangle with base as leg

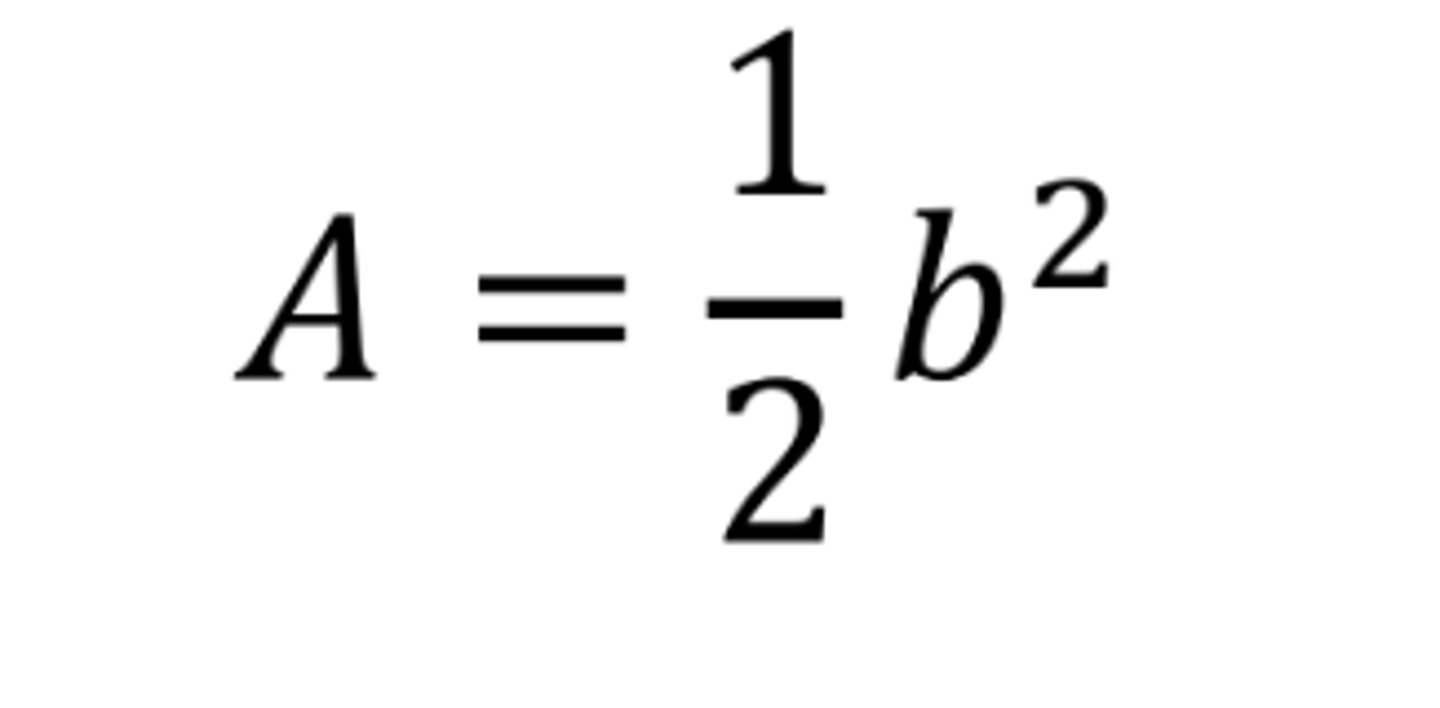
Area of Isosceles right triangle with base as hypotenuse

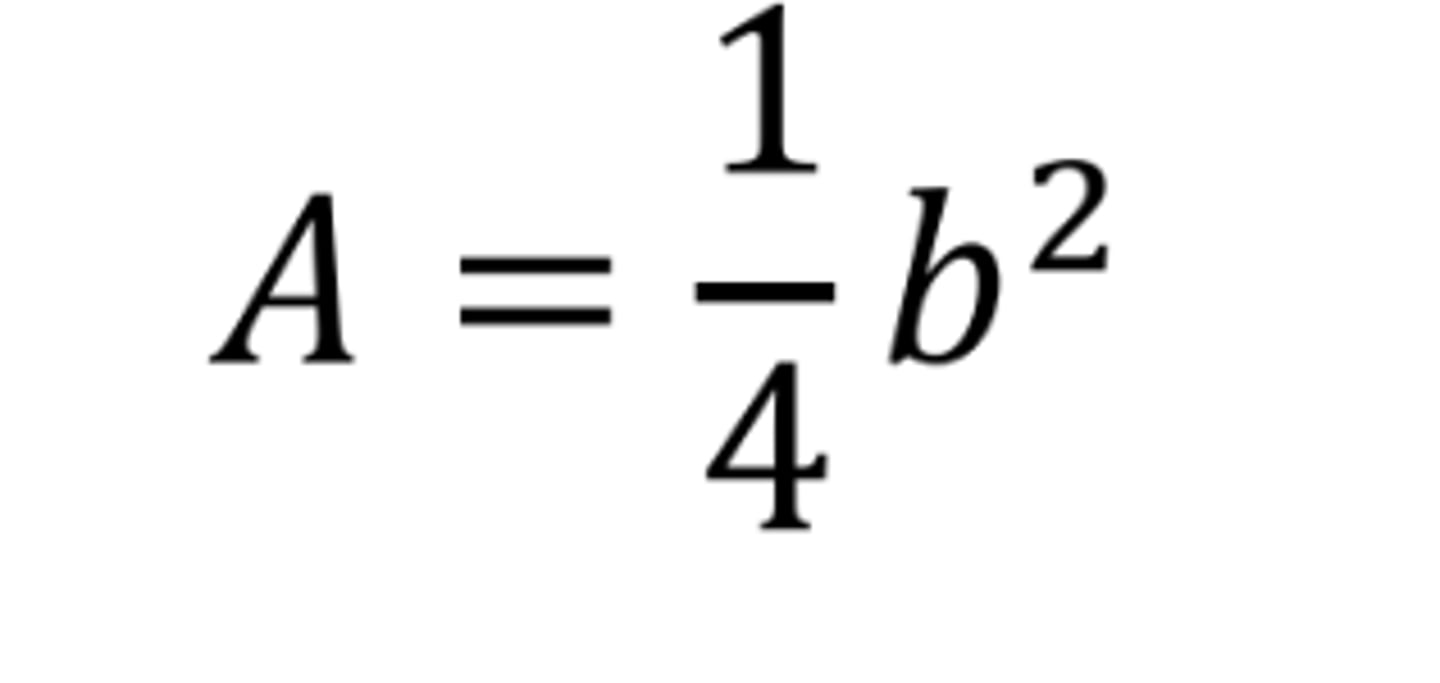
Area of equilateral triangle in terms of b

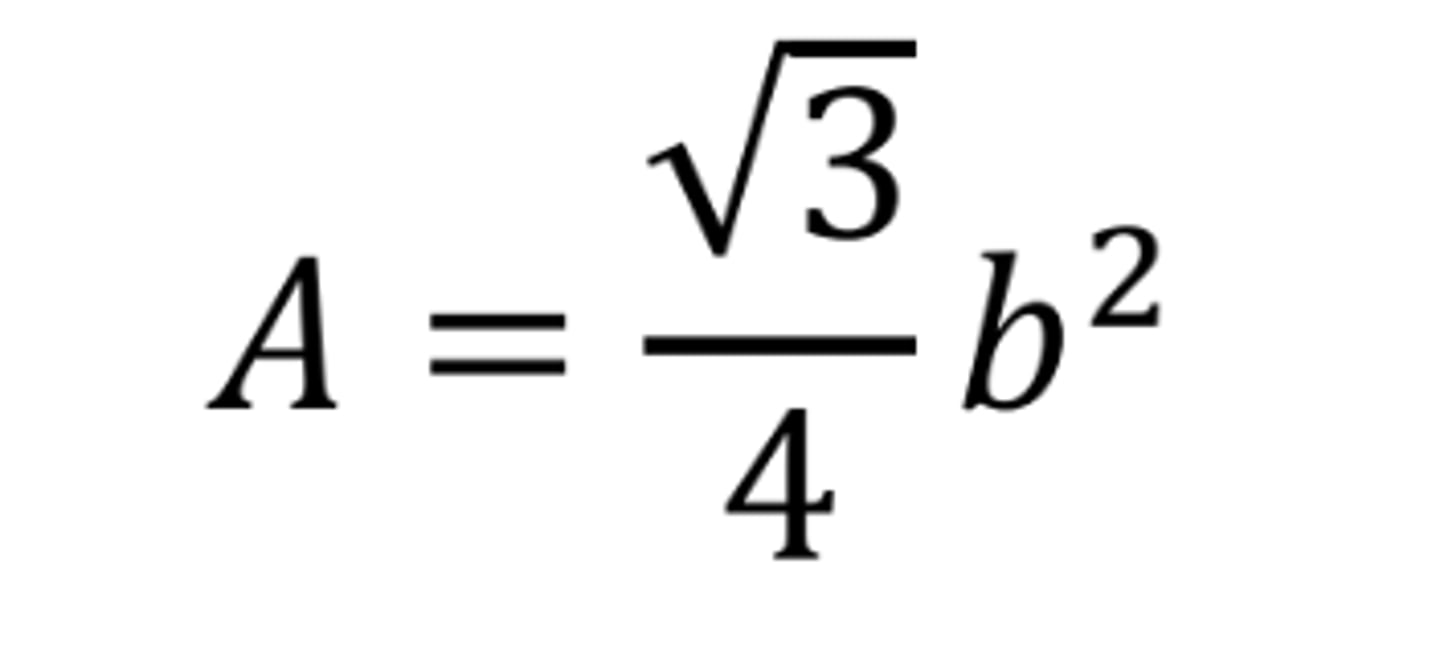
Relationship between x(t) or s(t), v(t) and a(t)

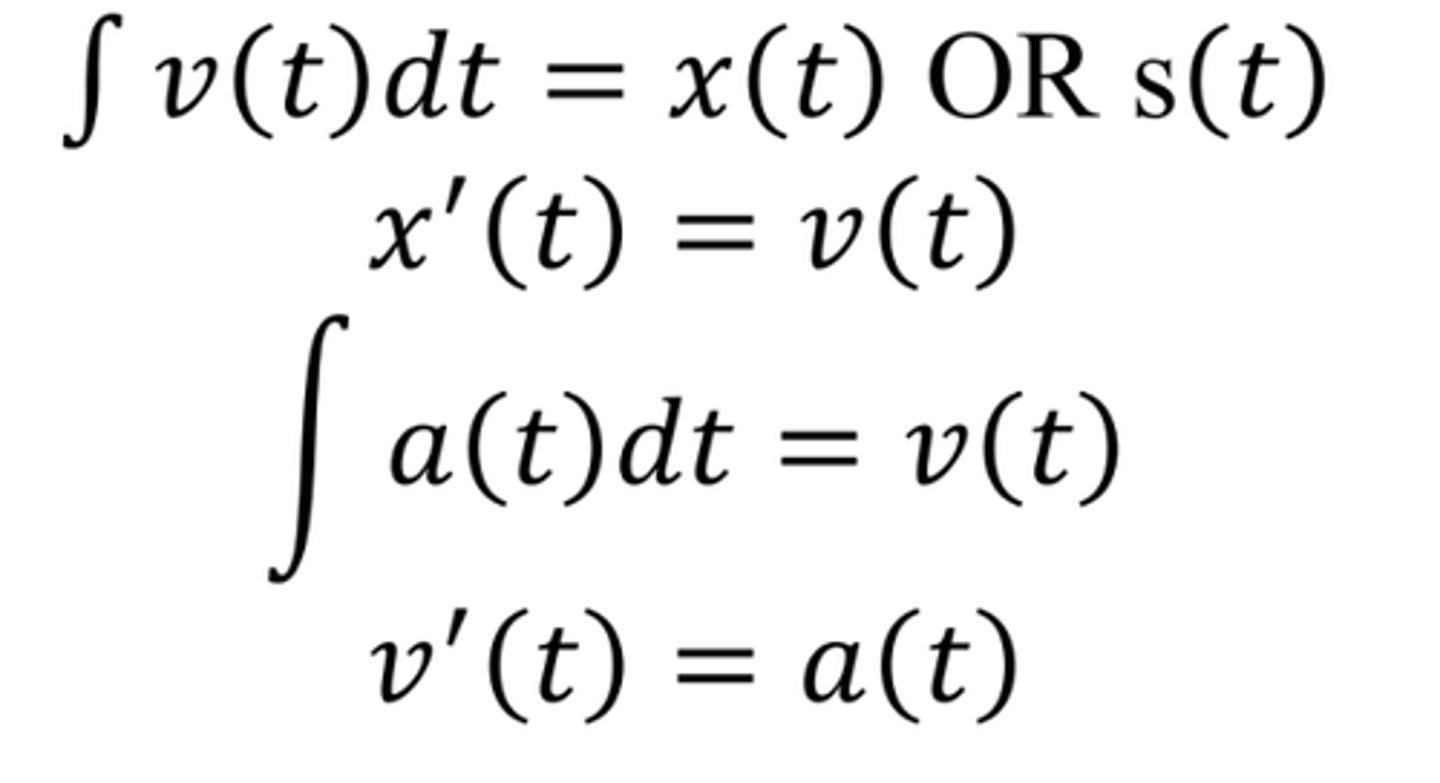
Total distance travelled from t = a to t = b

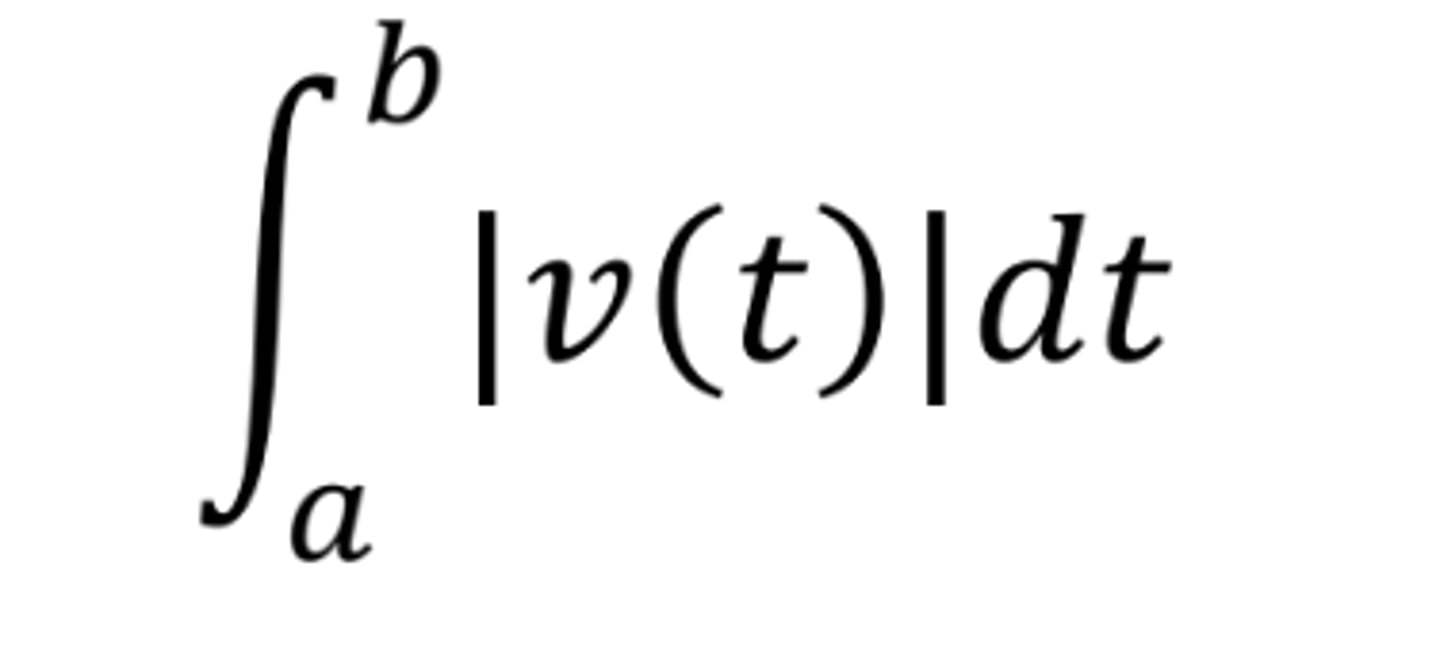
Displacement from t = a to t = b

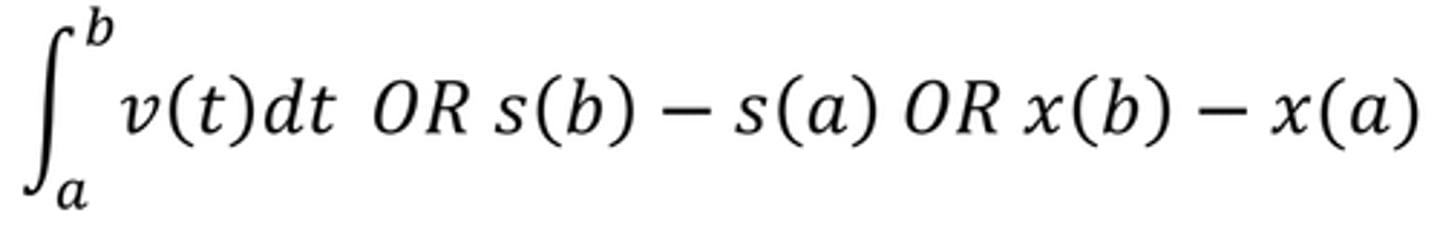
Definition of f(x) using the fundamental theorem of calculus