Parabola

Pre-Calculus — 1ˢᵗ Semester, Midterm

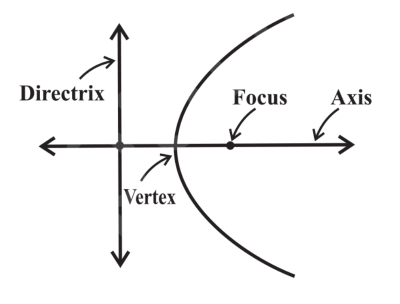
parabola

set of all points in a plane equidistant from a fixed point called the focus and a fixed line called the directrix

directrix

fixed line of a parabola

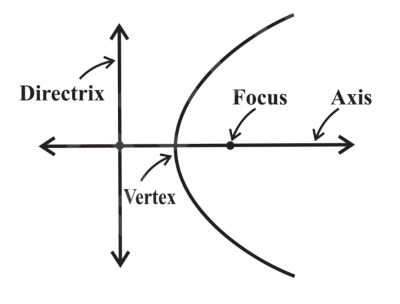
focus

fixed point of a parabola

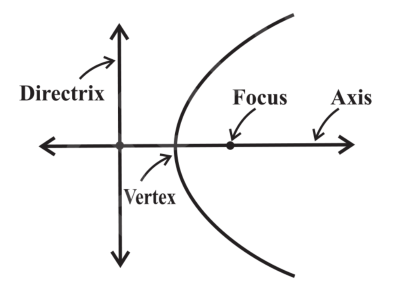
axis of symmetry

line that passes through the focus and is perpendicular to the directrix

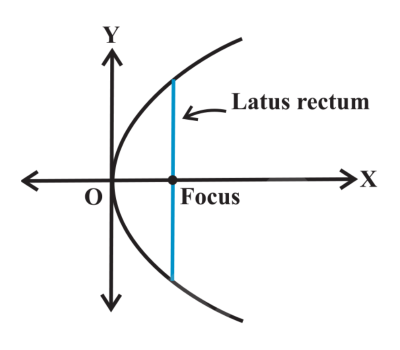
latus rectum

• chord that passes through the focus and is perpendicular to the axis of symmetry

• determines how wide the parabola is

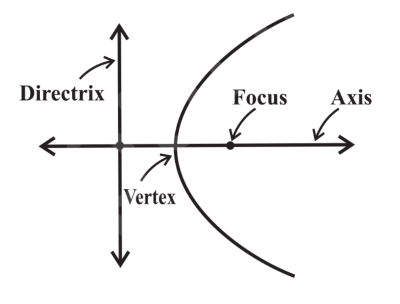
vertex

• midway between the latus rectum and the directrix

• point where the curve changes direction

• point of intersection

y² = 4px

equation of a parabola with horizontal axis of symmetry and vertex at (0, 0)

(p, 0)

focus of a parabola with horizontal axis of symmetry and vertex at (0, 0)

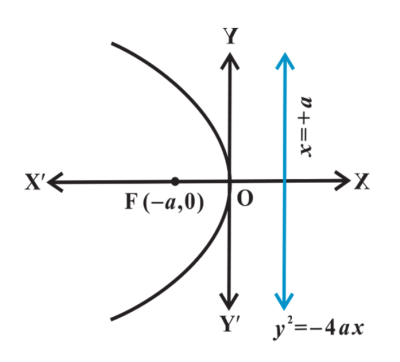
left

opening of a parabola if p < 0 with horizontal axis of symmetry and vertex at (0, 0) and (h, k)

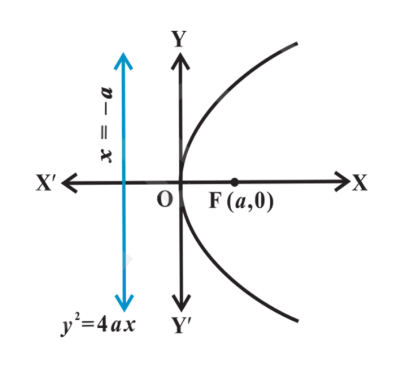
right

opening of a parabola if p > 0 with horizontal axis of symmetry and vertex at (0, 0) and (h, k)

(p, ± 2p)

endpoints of the latus rectum of a parabola with horizontal axis of symmetry and vertex at (0, 0)

x = -p

directrix of a parabola with horizontal axis of symmetry and vertex at (0, 0)

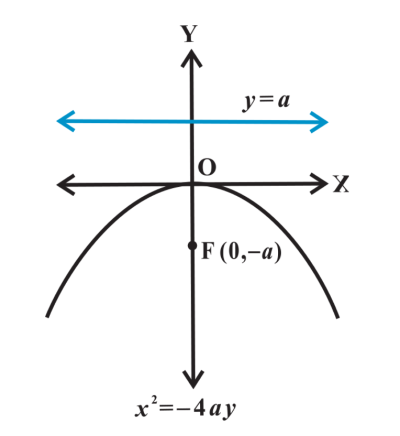
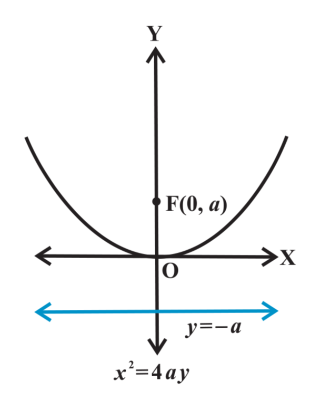
x² = 4py

equation of a parabola with vertical axis of symmetry and vertex at (0, 0)

(0, p)

focus of a parabola with vertical axis of symmetry and vertex at (0, 0)

downward

opening of a parabola if p < 0 with vertical axis of symmetry and vertex at (0, 0) and (h, k)

upward

opening of a parabola if p > 0 with vertical axis of symmetry and vertex at (0, 0) and (h, k)

(± 2p, p)

endpoints of the latus rectum of a parabola with vertical axis of symmetry and vertex at (0, 0)

y = -p

directrix of a parabola with vertical axis of symmetry and vertex at (0, 0)

(y - k)² = 4p (x - h)

equation of a parabola with horizontal axis of symmetry and vertex at (h, k)

(h + p, k)

focus of a parabola with horizontal axis of symmetry and vertex at (h, k)

(h + p, k ± 2p)

endpoints of the latus rectum of a parabola with horizontal axis of symmetry and vertex at (h, k)

x = h - p

directrix of a parabola with horizontal axis of symmetry and vertex at (h, k)

(x - h)² = 4p (y - k)

equation of a parabola with vertical axis of symmetry and vertex at (h, k)

(h, k + p)

focus of a parabola with vertical axis of symmetry and vertex at (h, k)

(h ± 2p, k + p)

endpoints of the latus rectum of a parabola with vertical axis of symmetry and vertex at (h, k)

y = k - p

directrix of a parabola with vertical axis of symmetry and vertex at (h, k)