Data Analysis Exam Review

Hypothesis

Null hypothesis

X does not cause Y or is not associated with Y

Type I error

False positive (wrongly rejecting a null hypothesis)

Type II error

False negative (failure to reject a null hypothesis that ought to be rejected)

Statistical significance

Allows us to measure whether data we observe is attributable to random chance alone

Descriptive data

Meant to reflect some truth about the world as it is

Mean

The average, x̄, or result of adding up all numbers (n) in a given set, then dividing by the number of numbers

Median

The middle, or the number in the middle when all numbers in a given set are arranged from smallest to largest

Mode

The most common or repeated observations

Normal distribution

Data that are distributed normally are symmetrical around their mean in a bell shape

Standard Deviation

Measure of how disperse the data are from their mean; how spread out the observations are - assigns a single number to a dispersion around the mean

The _ the standard deviation, the closer the data points tend to be to the mean

Lower

The lower the standard deviation, the ____ the data points tend to be to the mean

Closer

Standard error

Measure of the dispersion of the sample means (in the underlying population)

The standard error=

Standard deviation of the sample means

Large standard error

Sample means are spread out widely around the population mean

Small standard error

Sample means are clustered relatively tightly around the mean; so the more representative it is of the overall population

Ordinal Variables

Have a clear order to them; can be ranked

Ordinal Variable Eg.

Party ID ordered from left (1=Strong Democrat) to right (7=Strong Republican)

Categorical Variables

Observations correspond to categories/classes that do not necessarily have intrinsic ordering

Categorical Variable Eg.

Male vs female (0, 1)

Numerical Variables

Exact numbers that are evenly spaced apart

Numerical Variables Eg.

Exact income in dollar amounts, age, etc.

Formula for formulas in Excel

= FORMULA NAME(range: in parentheses)

Correlation

Measures the degree to which two phenomena are related to one another

Two variables are positively correlated if

A change in one is associated with a change in the other in the same direction

Two variables are negatively correlated if

A change in one is associated with a change in the other in the opposite direction

Correlation coefficient

Encapsulates the association between two variables in a single descriptive statistic

Correlation of 0 (or close to it)

Variables have no meaningful association with one another

Spurious correlation

Two variables appear to be directly related, but a hidden third variable actually influences both, or when the relationship exists purely by coincidence without any underlying causal mechanism

Expected value (or payoff)

Sum of all the different outcomes, each weighted by its probability and payoff; tells you whether a particular event is "fair," given its price and expected outcome

P-Value

A number between 0 and 1 that expresses the probability that the null hypothesis is true

Probability

Study of events and outcomes involving an element of uncertainty; not about the world we see, but about all the possible worlds

"Black swan" events

When events that may occur only "very rarely" do eventually happen

Expected Value

Way to more precisely understand the value of a decision - a shorthand for understanding the stakes of a choice

Calculate Expected Value

Weigh (multiply) all possible outcomes by their probability and payoff and then sum them

Law of Large Numbers

The more independent observations you draw randomly from a population, the closer the mean of those observations will get to the mean of the population

Selection bias

When mechanism for sorting individuals into one group or the other is not random; participants are not representative of the population

Publication bias

Positive findings are more likely to be published than negative findings, which can skew the results that we see

Recall bias

When participants do not remember previous events or experiences accurately; recalling the past based on the present or things that have since happened

Survivorship bias

When researchers focus on individuals, groups, or cases that have passed some sort of selection process while ignoring those who did not

Healthy user bias

People who faithfully engage in activities that are good for them are fundamentally different from those who don't

Central Limit Theorem

"A large, properly drawn sample will resemble the population from which it is drawn" - If we know about a population, we can make inferences about a sample, and vice-versa

Causal inference

Study of what we can learn about whether X causes Y, and if so, what effects X has on Y (causal hypothesis)

Experiments

Most common and strong way to learn about the effect of X on Y

Causal Effect

Compares the outcomes of different treatment values to quantify the impact of a treatment

Causal Effect Formula

Yi(1) - Yi(0)

Confounders

Things we do not directly observe that may be affecting the relationship we are interested in

Some experimental basics

Treatment, Subjects or participants, Potential outcomes, Average treatment effect/average causal effect, Randomization

Average treatment effect (ATE)

Average of the causal effects (treated potential outcome - untreated potential outcome) for all subjects

Three core assumptions of experimental analysis

Randomization, Noninterference, Symmetry

Randomization

Allows us to assume that potential outcomes are unrelated to pre-treatment covariates or characteristics

Noninterference

Each subject's potential outcomes reflect only whether that subject is treated or not -- a subject's potential outcomes are not affected by the treatments that other subjects receive

Symmetry

Identically structured treatments

Compliance

Whether or not people completed their assignment

Intent-to-Treat (ITT)

All participants who were enrolled and randomly allocated to treatment are included in the analysis and are analyzed in the groups to which they were randomized

Attention

Were people paying attention to your study? Or did they just give you a random number to make you happy?

Pre-registration

Declaring your expectations in advance of what you'll find

Demand effects

People infer what you're trying to do and respond accordingly

T-test

Determines whether the mean difference between two groups (experiment and control/placebo) is statistically significant

If the t-test is a value higher than 1.96 OR lower than -1.96

The associated p-value is .05 or less

Statistical significance p-value

0.5 or less

T-test formula for experimental data

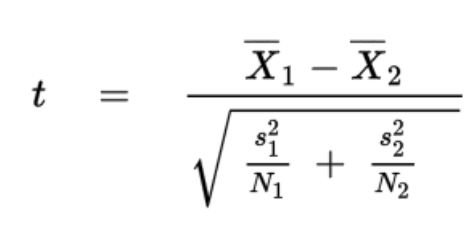
Regression

Tool used to understand relationships between independent and dependent variables

Regression Equation

Y = a + bX

Y in Regression Equation

The outcome variable we are interested in (dependent variable)

X in Regression Equation

Independent variable

a in Regression Equation

The y-intercept (the value for x when y is zero)

b in Regression Equation

The coefficient associated with each X independent variable

Bivariate Regression

Just one dependent and one independent variable

Multivariate Regression

One dependent variable and many independent variables

Regression Coefficient

Measures the average change in the Y variable if the X variable changes, holding everything else constant

R Squared (R^2)

Measures the amount of variation in the Y that is explained by your regression

0 in R^2

None of the Y is explained by your regression

1 in R^2

All of Y is explained by your regression

Confidence interval

Gives an estimated range of values that is likely to include the "actual" number you are looking for

Types of variables

Categorical, Ordinal, Nominal, Dummy/binary, Continuous

Ordinal

Variables that can be ranked

Nominal

Variables that cannot be ranked

Dummy/binary

Variables that only have two types of observations (almost always 1's and 0's)

Continuous

Observations are numbers that have intrinsic ordering, with potentially infinite range (eg. height, weight)

Standardization

Achieved by converting everything into standard deviation units

Running a regression in R

Object name ← lm (dependent variable ~ independent variable, data = data set name)