academic legend

How are the cardinalities of the sets N of natural numbers, Q of rational numbers, and R of real numbers related to eachother?

|N| = |Q| < |R|

Which statement about the cardinalities of the set N of natural numbers and the set 2N of even natural numbers is correct?

|N| = |2N|

Which statement about the cardinalities of set A and its power set P(A) is correct?

|A| < |P(A)|

Recall our first proof of the theorem that regular languages are closed under intersection and union: We constructed a new DFA M based on the two DFAs M1 and M2. The new DFA M used pairs of states M1 and M2. Given that M1 and M2 have k1 and k2 states respectively. How many states does M have?

k1 * k2

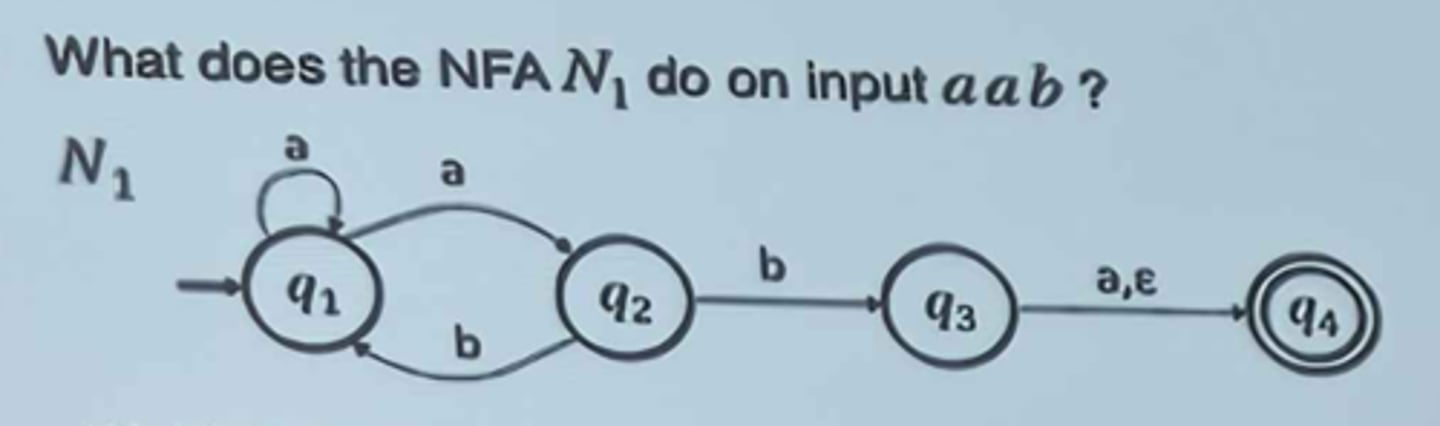
What does NFA N1 do on input aab?

Accept

In the proof of the theorem that languages recognized by NFAs are regular we constructed DFA M' based on an NFA M using the power-set of the states of M as the states of M'. If M has k states, how many states does M' have?

2^k

The proof of the pumping lemma for regular languages uses the fact that if DFA M has p states and it runs for more than p steps then this M will enter some state at least twice. We call this fact:

The Pigeonhole Principle

We used the Pumping Lemma to show that D = {0^k 1^k | k ≥ 0} is not regular. How can we show that B = {w | w has equal numbers of 0s and 1s} is not regular?

We know that 0*1* IS regular. If we assume that B is regular then 0*1* ∩ B = D should be regular as well.

Match the recognizer with the generator: DFA

regular expression

Match the recognizer with the generator: NFA

regular expression

Match the recognizer with the generator: PDA

context free grammar

Write the language of all sequences of characters from Σ = {0,1} that contain two consecutive 1s as a regular expression.

(0 U 1) o 1 o 1 o (0 U 1)

Regular languages are closed under intersection. (True/False)

True

Regular languages are closed under union. (True/False)

True

Regular languages are closed under concatenation. (True/False)

True

Which of the following is an application of the pumping lemma for regular languages?

Proving that a given language is not regular.

Context free languages are closed under union. (True/False)

True

Context free languages are closed under concatenation. (True/False)

True

Context free languages are closed under Kleene*. (True/False)

True

Regular languages are closed under complement. (True/False)

True

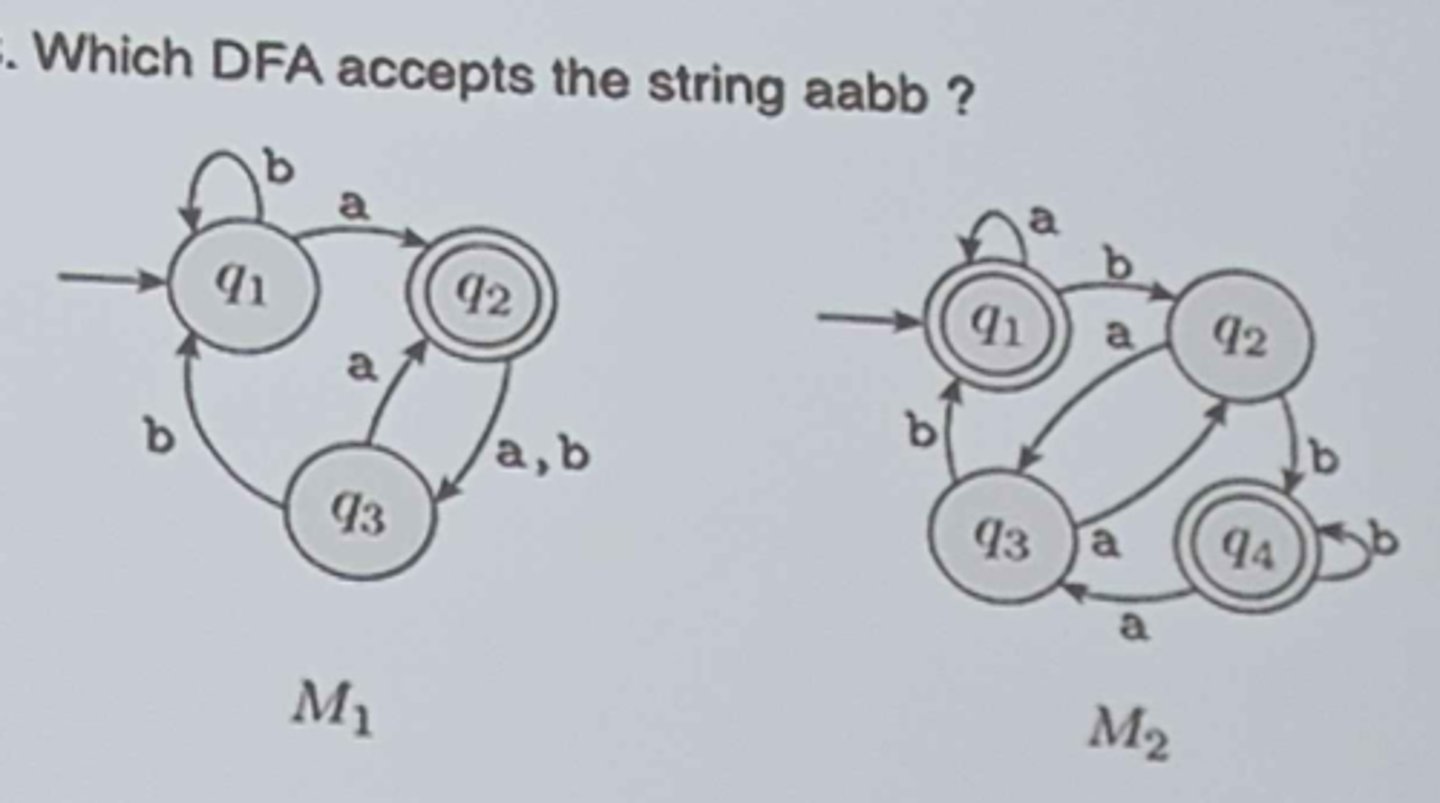
Which DFA accepts the string aabb?

M2 but not M1

Can you show that every NFA can be converted to an equivalent one that has a single accept state?

Yes, by adding a new state q and then adding ε-transitions from each accept state to q. The new state q will be the single accept state of the new NFA.

Regular languages are closed under Kleene*. (True/False)

True

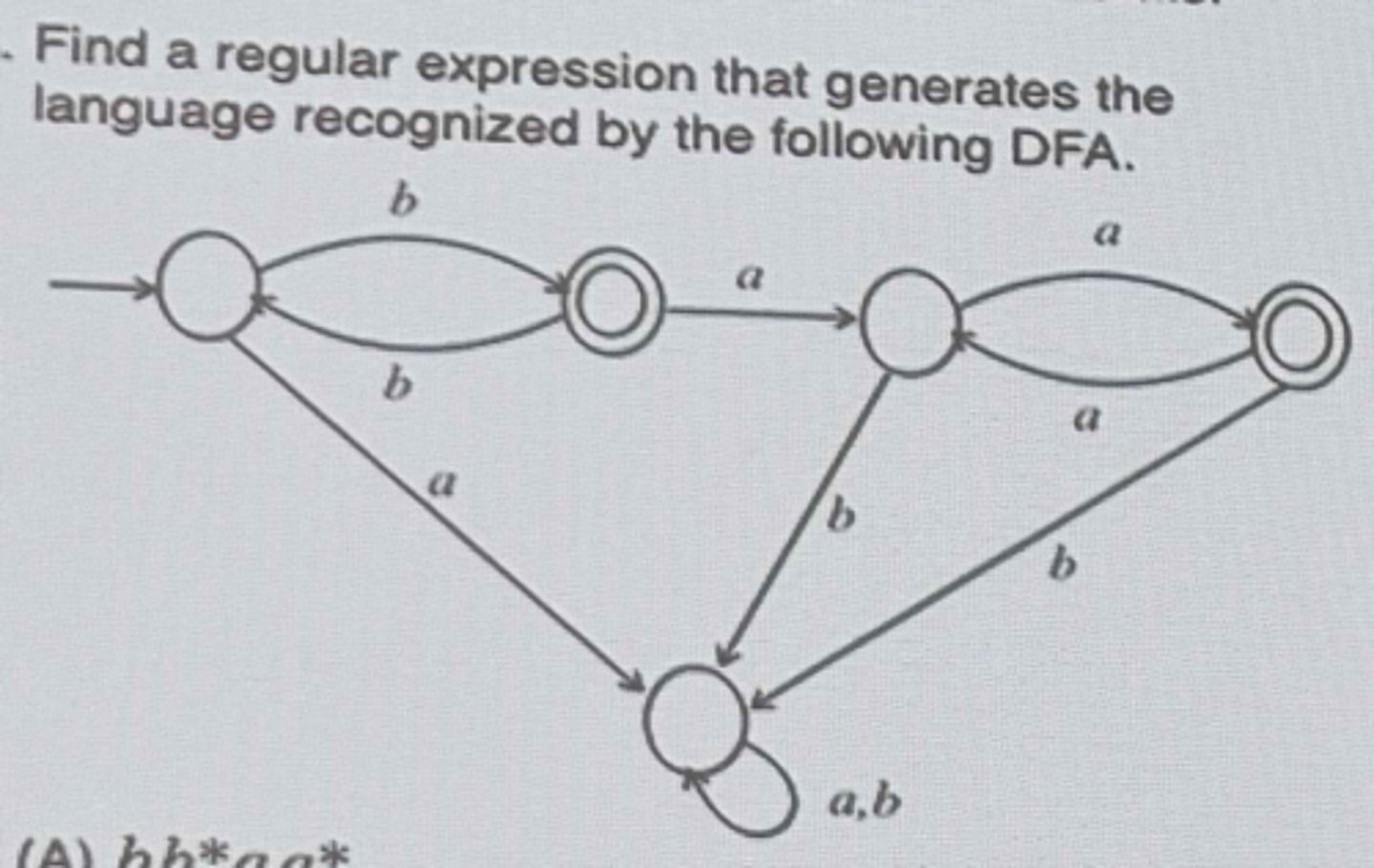
Find a regular expression that generates the language recognized by the following DFA.

b(bb)(aa)

Swapping the accepting and non-accepting states of a DFA shows that regular languages are closed under complement. However, swapping the accepting and non-accepting states of an NFA doesn't necessarily yield an NFA that recognizes the complement. Does that indicate that the class of languages recognized by NFAs is not closed under complement?

No, since NFAs and DFAs recognize the same class of languages.

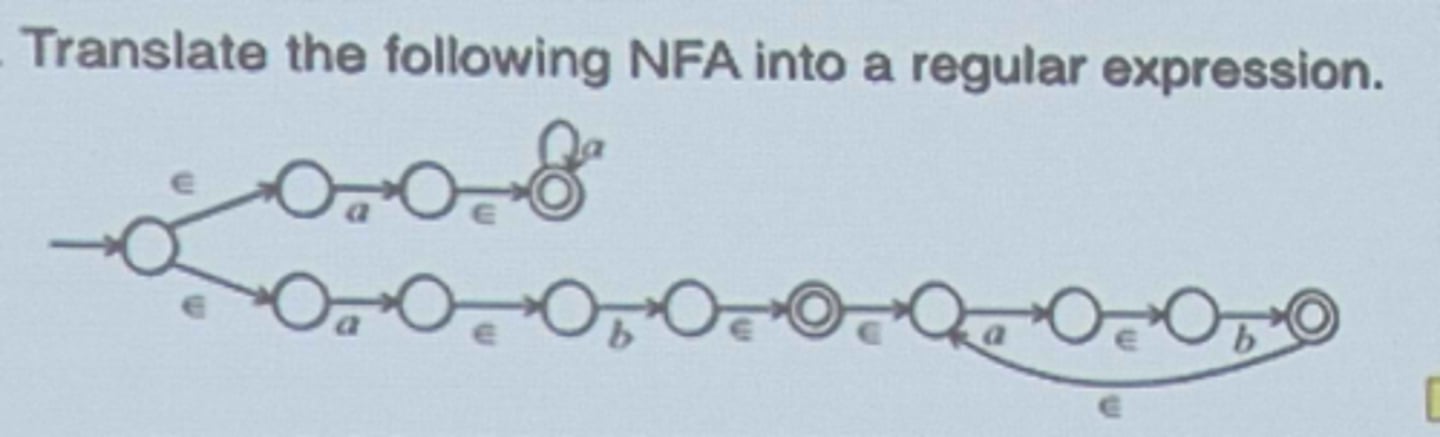
Translate the following NFA into a regular expression.

aa* ∪ ab(ab)*

What is the definition of an alphabet Σ?

Σ is an non-empty, finite set.

Which of the following is a property of a DFA?

It can accept ε (the empty string).

Select all of the strings that are in L(G). Select all that apply.

ε

001101

000111

Which of the following is a difference between a DFA and a NFA? (2 answers)

An NFA can allow ε-transitions, a DFA does not.

A DFA has one state transition for each input symbol, but an NFA can have zero or many transitions per input symbol.

Which of the following is an advantage of using an NFA instead of a DFA?

NFAs are simpler to combine (e.g. union, concatenation, Kleene*) than DFAs.

What is a formal language?

A set of strings over a finite alphabet.

Which of the following is a property of deterministic finite automata (DFA)?

It cannot perform ε-transitions.

What characterizes a context-free grammar?

Production rules with a single non-terminal on the left hand side.

Which of the following languages is not recognized by deterministic finite automaton (DFA)?

{a^n b^n | n ≥ 0}

Which of the following best describes a pushdown automaton (PDA)?

A computational model that uses a stack to keep track of symbols.

What is the pumping lemma for regular languages used to prove?

That a given language is not regular

What is a Deterministic Finite Automaton (DFA) used for?

To recognize regular languages

What is the role of the stack in a pushdown automaton?

To store intermediate results during computation

Which of the following best describes a Non-deterministic Finite Automaton (NFA)?

An automaton where multiple transitions are possible from a single state for the same input symbol

What is the difference between DFAs and NFAs?

NFAs can have multiple transitions for the same input symbol and state

Which of the following classes of languages can be recognized by a pushdown automata (PDA)? (Two answers)

Context-free languages

Regular languages

What is the primary function of a context-free grammar (CFG)?

To generate strings in a context-free language.

Which of the following is a characteristic of context-free languages?

They can be recognized by pushdown automata

What is the primary role of transitions in a finite automaton?

To define the movement between the states based on input symbols

Which of the following statements is true about the Pumping Lemma?

It can be used to prove a language is not regular.

Which of the following is not a component of a pushdown automaton?

Tape

What is the distinguishing feature of a regular language?

It can be recognized by a deterministic finite automaton

Which of the following automata is the most powerful in terms of language recognition?

Pushdown automaton

What is the purpose of the transition function in a finite automaton?

To define the movement between states based on input symbols

Which of the following statements is FALSE regarding the conversion of a non-deterministic automaton (NFA) to a deterministic finite automaton (DFA)?

NFAs are more expressive than DFAs.

Which of the following languages is not context-free?

{a^n b^n c^n | n ≥ 0}

In context-free grammars, what are terminals? (2 answers)

Symbols that cannot be replaces by production rules

Symbols from the output alphabet

Which of the following is NOT a valid context-free grammar?

Sb -> aSbS | ε

Which of the following statements is true about regular expressions?

They can express any regular language

Which of the following is an example of a NON-regular language?

{w | w contains an equal number of 0s and 1s}

What is the main purpose of a start symbol in a context-free grammar?

To represent the starting point of a derivation

In a pushdown automaton, what does the top of the stack represent?

The most recently pushed symbol

Match the Bachmann-Landau asymptotic notation with the correct definition:

1. ∃ k > 0 ∃ n0 ∀ n > n0 : |f(n)| ≤ k g(n)

2. ∃ k > 0 ∃ n0 ∀ n > n0 : f(n) ≥ k g(n)

3. ∀ k > 0 ∃ n0 ∀ n > n0 : |f(n)| < k g(n)

4. ∃ k1 > 0 ∃ k2 > 0 ∃ n0 ∀ n > n0 : k1 g(n) ≤ f(n) ≤ k2 g(n)

a. f(n) ∈ O(g(n)) WORST CASE

b. f(n) ∈ Θ(g(n)) AVERAGE CASE

c. f(n) ∈ Ω(g(n)) BEST CASE

d. f(n) ∈ o(g(n)) LOOSE UPPER BOUND

1 -> a

2 -> c

3 -> d

4 -> b

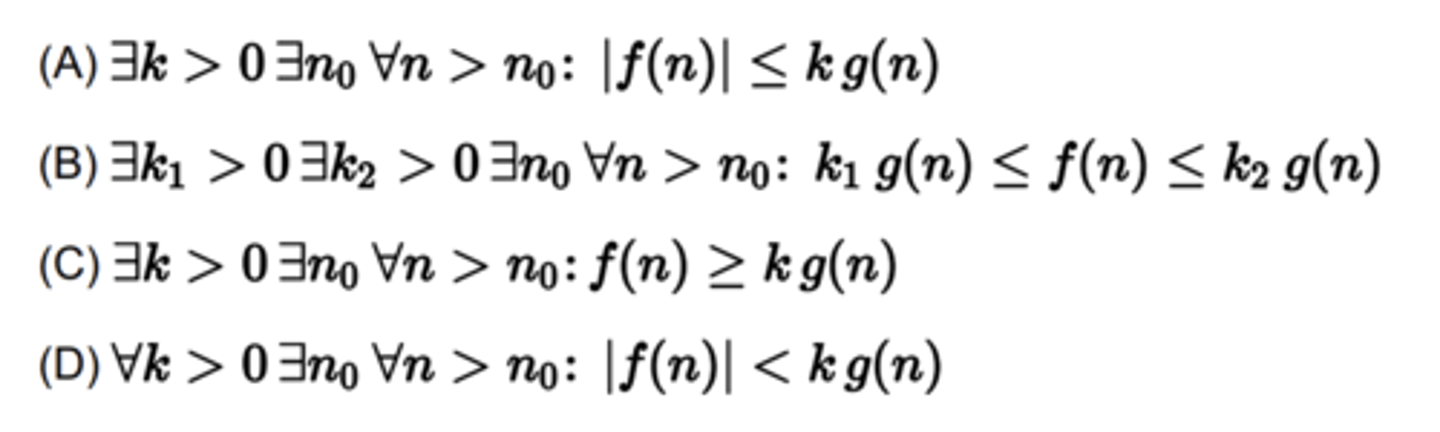
What is the known relationship between the complexity classes N and NP?

P ⊆ NP

A language A ⊆ Σ* is polynomial time/mapping reducible to a language B ⊆ Γ* and we write A ≤ mB

if there is a computable function f: Σ -> Γ in such that w ∈ A <=> f(w) ∈ B

Is it true that TIME(t(n)) SPACE(t(n))?

Yes, because we need at least one computational step to write into a new memory cell

A language B is NP Complete iff

B is in NP and any language A in NP can be polynomially reduced to B.

Which of these languages are NP-Complete? (2 answers)

SAT (Boolean Satisfiability)

3-SAT (3-CNF Boolean Satisfiability)

If we could find a proof that SAT ∊ P then this would imply that

P = NP

Are all regular languages in the complexity class P?

Yes, because a DFA reads one input symbol per state transition.

How can we describe the complexity classes P and NP informally?

NP = all languages we can verify membership quickly

P = all languages where we can test membership quickly

Which of the following boolean expressions are in 3-CNF? (2 answers)

1. (x ^ ȳ ^ z) V (x ^ y ^ z) V ( x ^ ȳ ^ z̄ )

2. (ū ^ ȳ ^ z) V (x ^ v ^ z) V (x ^ ȳ ^ wˉ)

3. (u ^ ȳ ^ z) ^ (x ^ v ^ z) V (x V ȳ V wˉ)

4. (x ^ ȳ ^ z) ^ (x ^ y ^ z) V (x V ȳ V wˉ)

2 - ū ^ ȳ ^ z) V (x ^ v ^ z) V (x ^ ȳ ^ wˉ)

4 - (u ^ ȳ ^ z) ^ (x ^ y ^ z) V (x V ȳ V wˉ)

Is SAT in NP? (Yes/No)

Yes.

Two models of computation are polynomial related if each can simulate the other, i.e., if the computation takes t(n) time on one model, it make take t^k (n) time on the other model, for some k.

Which of the following are polynomially related to 1-tape Turing Machine? (4 answers)

multi-tape TMs

multi-dimensional Turing Machines

random access machines (RAM)

cellular automata

Alan Turing proved the undecidability of the halting problem. Which proof technique from set theory did inspire Turing?

Cantor's diagonal argument

Which of the following languages are decidable? (3 answers)

1. Acceptance problem for NFAs (A NFA) = {

2. Acceptance problem for DFAs (A DFA) = {

3. Equivalence problem for DFAs (EQ DFA) = {

4. Acceptance problem for TMs (A TM) = {

1 - Acceptance problem for NFAs (A NFA) = {

2 - Acceptance problem for DFAs (A DFA) = {

3 - Equivalence problem for DFAs (EQ DFA) = {

What does the Church-Turing-Thesis claim?

Any real-world computation can be translated into an equivalent computation performed by a Turing machine.

Decidability of languages does not depend on the model of computation. (True/False)

True

Languages in P can be efficiently decided.

Not necessarily. The time complexity might be O(n^k) with a very large value for k

Which of the following statements are correct: (3 answers)

1. All regular languages are in the complexity class P.

2. All decidable languages are in the complexity class P.

3. All languages in P are T-recognizable.

4. All languages in P are decidable.

1 - All regular languages are in the complexity class P.

3 - All languages in P are T-recognizable.

4 - All languages in P are decidable.

Is the complexity class P closed under union, i.e. does L1 ∈ P and L2 ∈ P imply L1 ∪ L2 ∈ P?

Yes.

Is the following formula satisfiable? (Yes/No)

(x V y) ^ (x V ȳ) ^ (x̄ V y) ^ (x̄ ^ ȳ)

No

Which of the following are true? (3 answers)

1. 3^n ∈ 2^(O(n))

2. n log n ∈ O(n^2)

3. n^2 ∈ O(n)

4. 2n ∈ O(n)

1 - 3^n ∈ 2^(O(n))

2 - n log n ∈ O(n^2)

4 - 2n ∈ O(n)

Is SPACE(t(n)) ⊆ TIME(2^O(t(n)))?

Yes, because a TM that uses t(n) tape cells cannot use more than 2 ^ O(t(n)) time without repeating a configuration and thus looping and not halting.

What is the output (on the tape) of the Turing Machine M on input 10010111 where M = (Q, Σ, Γ, δ, q_0, q_acc, q_rej)

states Q = {right, carry, done}

input alphabet Σ = {0, 1}

tape alphabet Γ = {1, 0, ' '}

start state q0 = right

accept state q_acc = done

and transition function δ : Q x Γ -> Γ x {L, R} x Q defined by

δ(right, 1) = (1, R, right)

δ(right, 0) = (0, R, right)

δ(right, ' ') = (' ', L, carry)

δ(carry, 1) = (1, L, carry)

δ(carry, 0) = (0, L, done)

δ(carry, ' ') = (' ', L, done)

10011000

Recall the Pumping Lemma for CFLs:

Let Σ = {0, 1} and F = {ww | w ∈ Σ*}

In order to show that F is not context free, which value should we use for the string S to find a contradiction?

s_2 = 0^p 1^p 0^p 1^p ∈ F

Let A1 = {0^k 1^k 2^L | k, l ≥ 0} (equal #s of 0s and 1s).

Let A2 = {0^L 1^k 2^k | k, l ≥ 0} (equal #s of 1s and 2s).

Observe that both A1 and A2 are CFLs. What can we now conclude?

The class of CFLs is not closed under intersection

Context free languages are closed under intersection. (True/False)

False

Match the language with the smallest class that its contained in:

1. E = Ø

2. S = {ε}

3. A_TM = {

4. L1 = {a^k | k ∈ N0}

5. L2 = {a^k b^k | k ∈ N0}

6. L3 = {a^k b^k c^k | k ∈ N0}

a. context free

b. decidable

c. regular

d. finite

e. empty

f. t-recognizable

1 - empty (e)

2 - finite (d)

3 - t-recognizable (f)

4 - regular (c)

5 - context free (a)

6 - decidable (b)

All languages are regular. (Yes/No)

No

Regular languages are closed under union and intersection. (True/False)

True

GNFAs, NFAs, and DFAs are all equivalent, i.e. they all recognize the same class of languages.

Yes, they all recognize regular languages.

Are all context-free grammars regular? (Yes/No)

No

The complexity class P does depend on the model of computation

Yes, but it is equivalent for all reasonable deterministic models of computation.

In our proof of the theorem that languages recognized by NFAs are regular we constructed a DFA M' based on an NFA M using the powerset of the states of M. If M has n states, how many states does M' have by this construction?

2^n