Lecture 17 - Predator-Prey Model

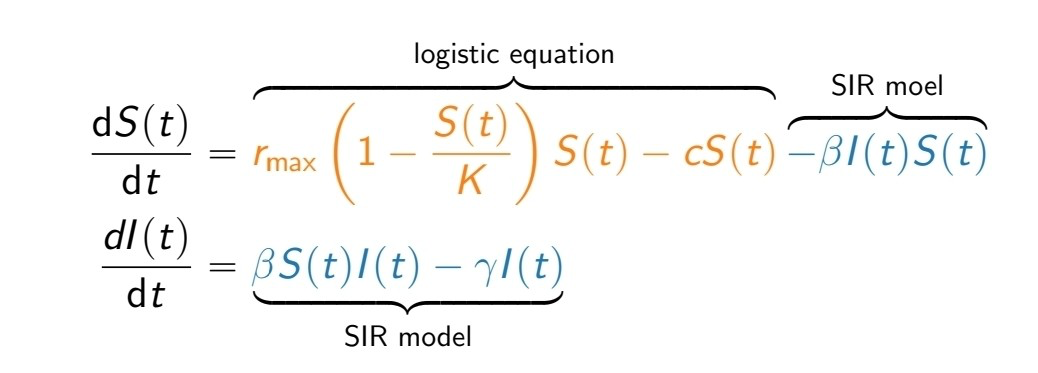
Endemic SI Model

Combines the logistic equation and the susceptible & infectious model from the SIR model. It aims to show how a disease may spread within a population that is still experiencing growth and death rather than a closed populatio

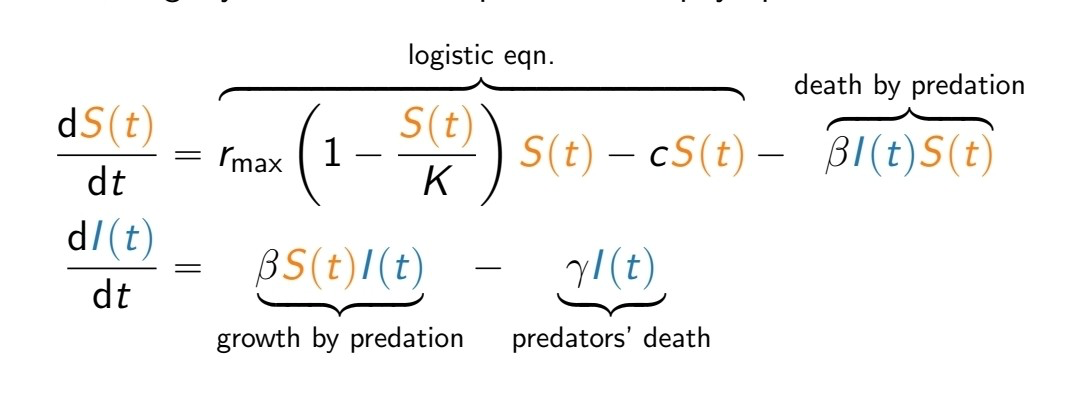
Prey-Predator Model

The same as the endemic SI model, but rather than having susceptible and infectious individuals, we’ll have prey and predator populations. In this case, S(t) would represent the prey population while I(t) would represent the predator population

• Beta would be predation rate (how many prey are lost by hunting by a single predator)

• Mu would be predator death rate

Predicting Predator-Prey Relationships 

With an initial population and all the parameters, we are able to predict how the prey and predator populations may continue. In a normal scenario, predator and prey are usually able to coexist together at two separate equillibriums. This is where their populations aren’t necessarily changing and are within an equillibrium.

Paradox of Enrichment

Describes how events that may elicit a change in the growth rate of prey can have unexpected outcomes.

Say, if we were to increase K by adding more resources for the prey population, this would obviously increase the prey’s growth rate. Because of this, we should expect the prey to have a higher equillibrium overall. However, this isn’t the case because increasing the prey’s population growth rate (more reproducing) would also increase the predator’s growth rate (βS(t)). Since there are more predators, they’ll apply more predation pressure onto the prey and this cancels out the increased growth rate from earlier.

• So, in the end, adding resources for prey wouldn’t really benefit prey population because the benefit it would have is cancelled out by the pressure from predators. Instead, predators are the ones benefitted, making it a paradox.