Module 3: Bivariate Data

What is bivariate data?

• 2 variables measured on the same experimental unit that come in data pairs (1 pair/experimental unit)

• Data pair is collected independently without bias

How can bivariate data occur? (3 different ways)

• 2 qualitative variables (ex: gender and major of college students)

• 1 qualitative and 1 quantitative (ex: gender and height)

• 2 quantitative variables (ex: height and shoe size)

How is data involving 2 qualitative variables showcased?

• Involves the usage of contingency table or side by side bar/circle graphs

  • Ex: survey on hair color and type

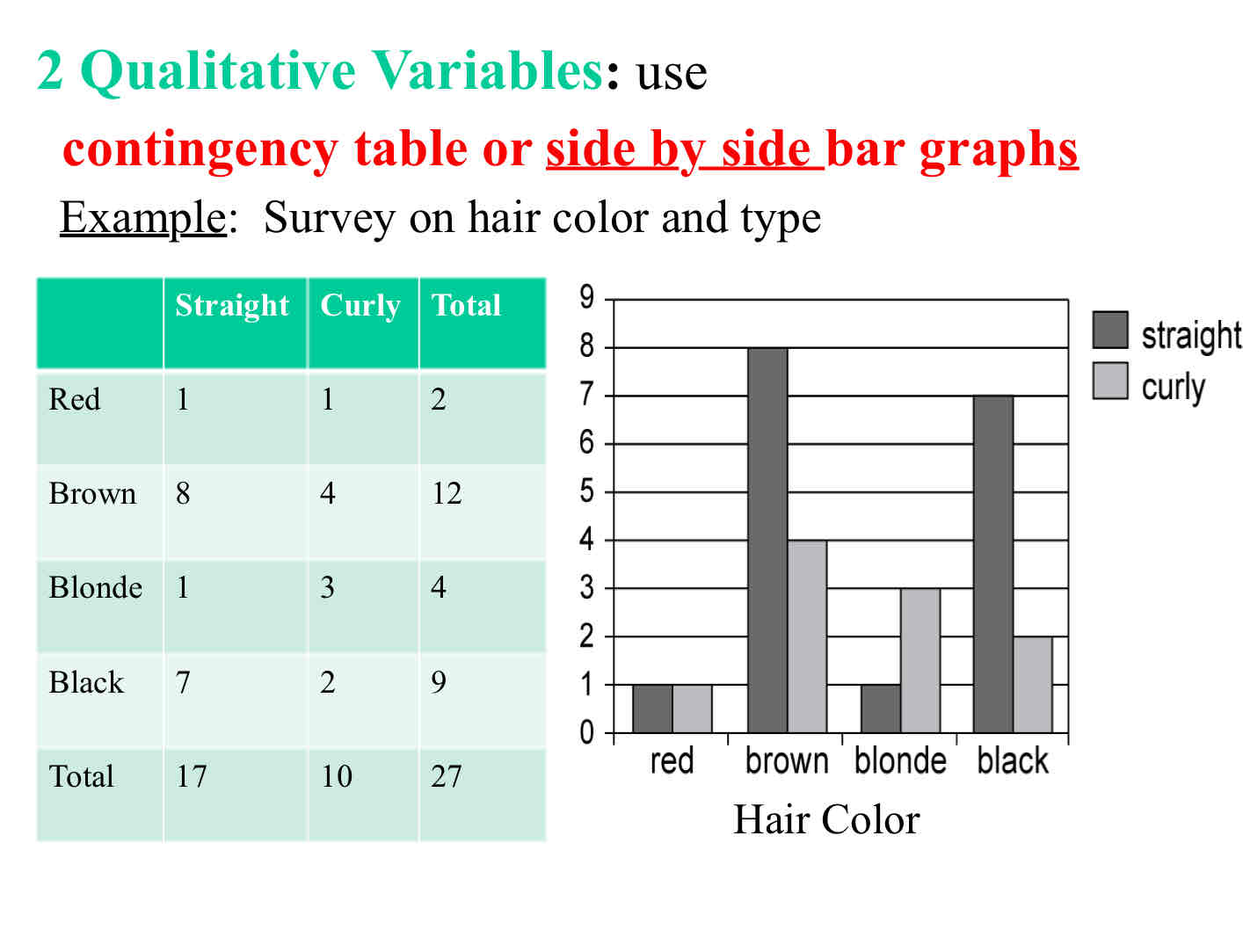
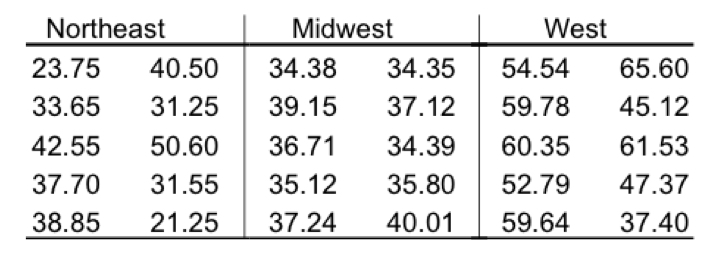
How is data involving 1 quantitative and 1 qualitative variable showcased?

Ex: region vs electric bill

Involves the use of side by side box and whisker graphs to display data

• Shows measures of center and spread for each qualitative outcome

Multiple stem and leaf plots or multiple frequency histograms can also be used

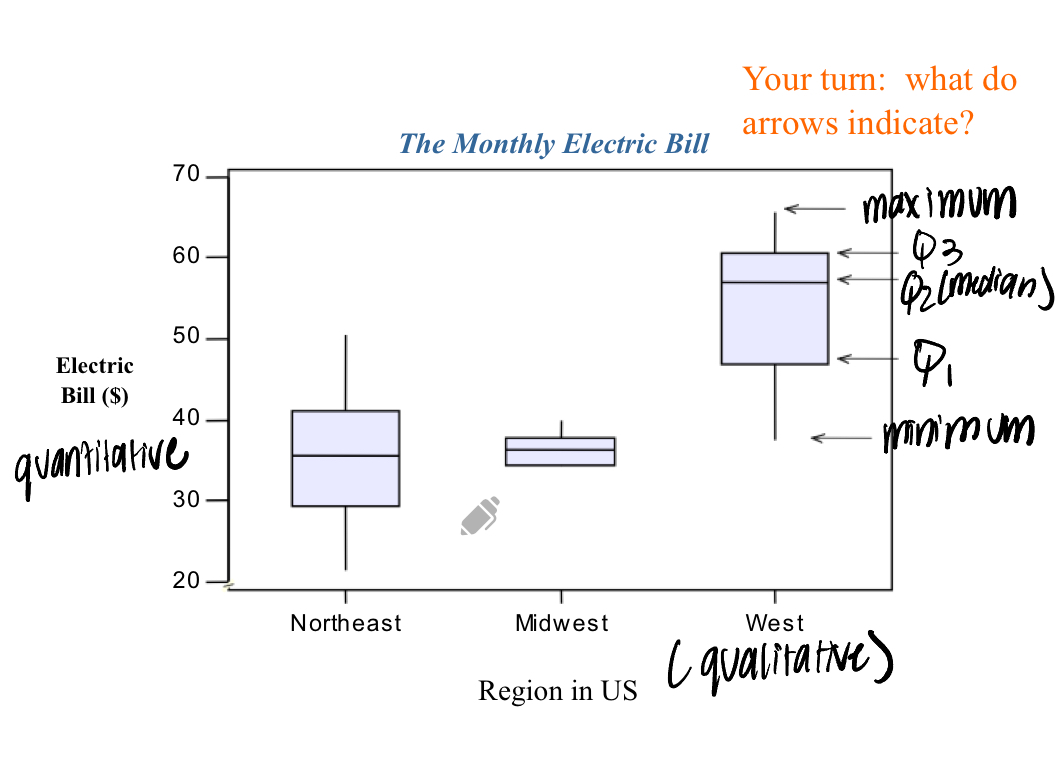
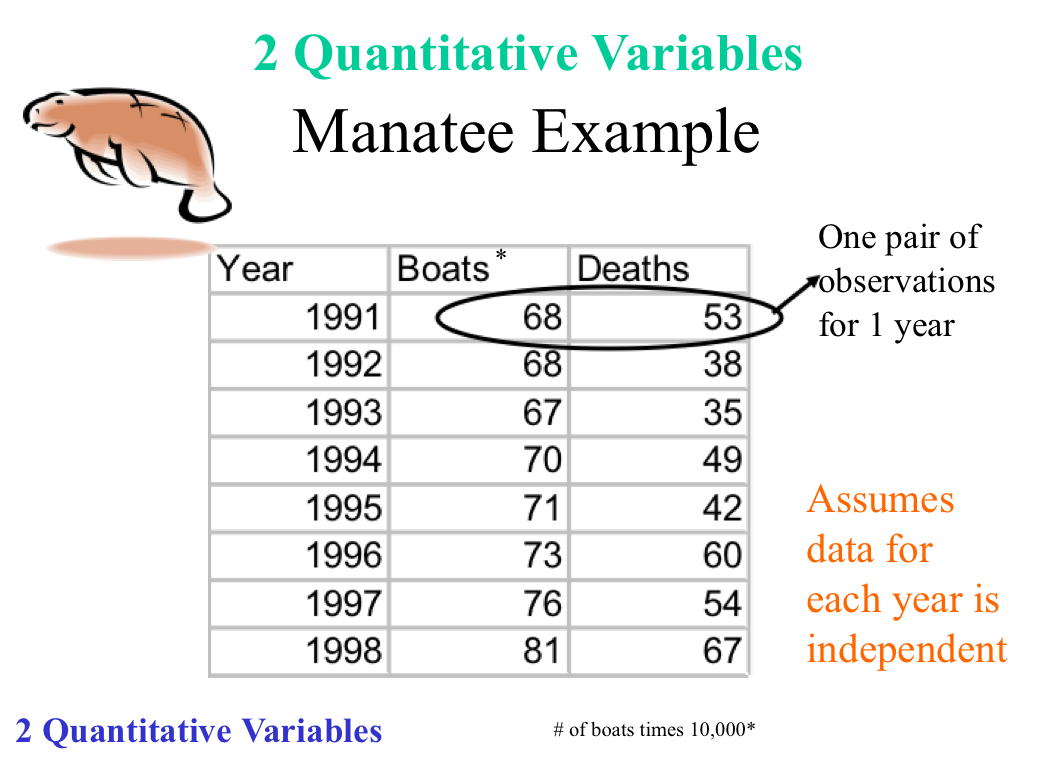
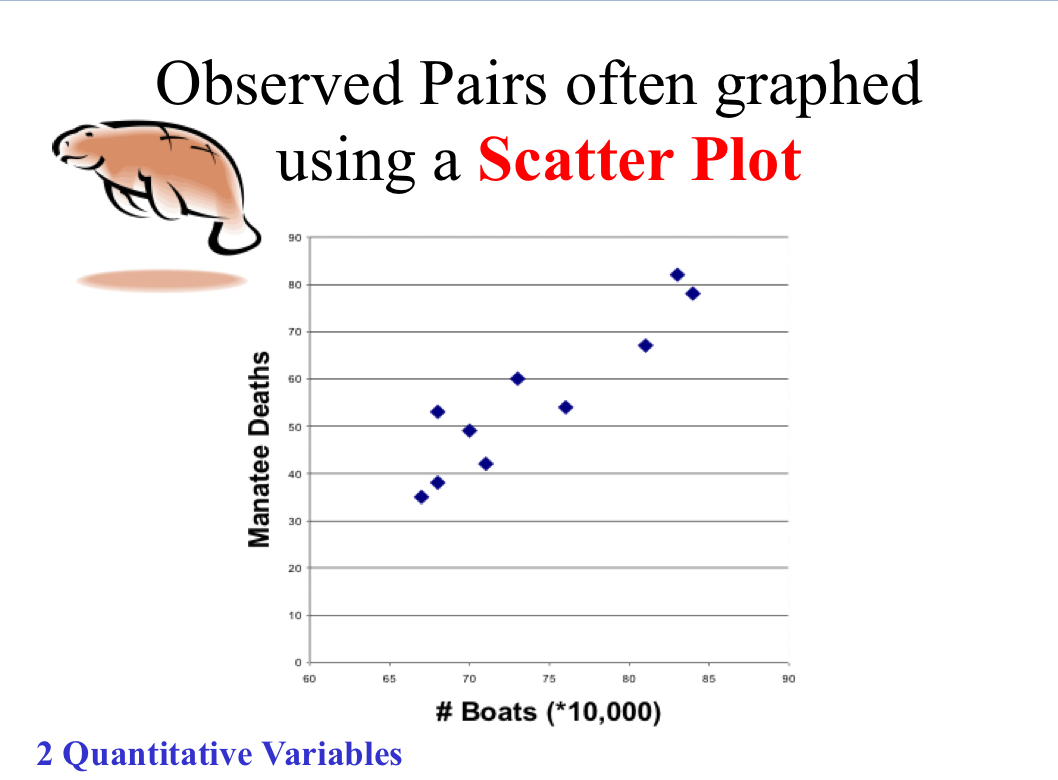
How is data involving 2 quantitative variables showcased?

Ex: Manatee deaths and # of boats per year

• Involves a scatter plot with data points

  • A data point represents two values (x and y variables)

How are 2 quantitative variables analyzed?

Using Correlation and Regression

Linear Correlation

• Requires a linear relationship between 2 quantitative variables

  • ONLY used if there is a linear relationship to analyze

  • Variables are interchangeable so if they are switched then the r will be constant

Correlation Coefficient

• Sample statistic coefficient is r

  • Measures the direction and strength of a linear relationship between 2 variables

  • Values vary from -1 to +1

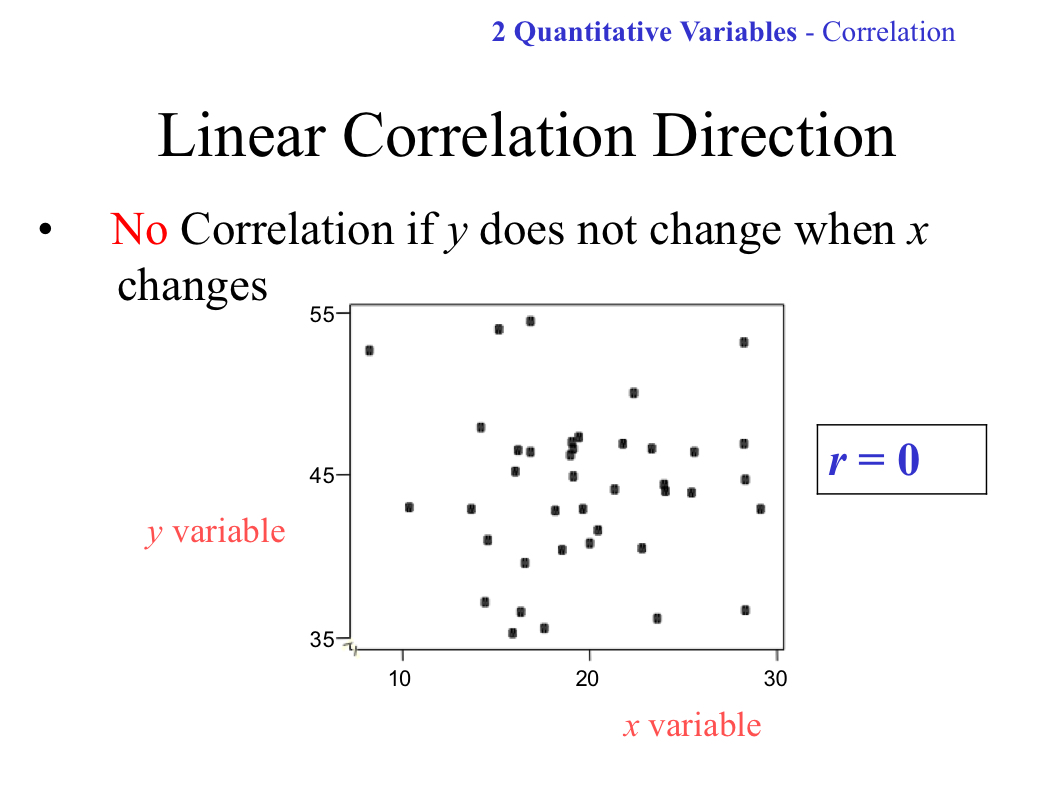
Linear Correlation Direction: No correlation

• Can be a scatter, r=0

• Indicates that there is no linear relationship between x and y

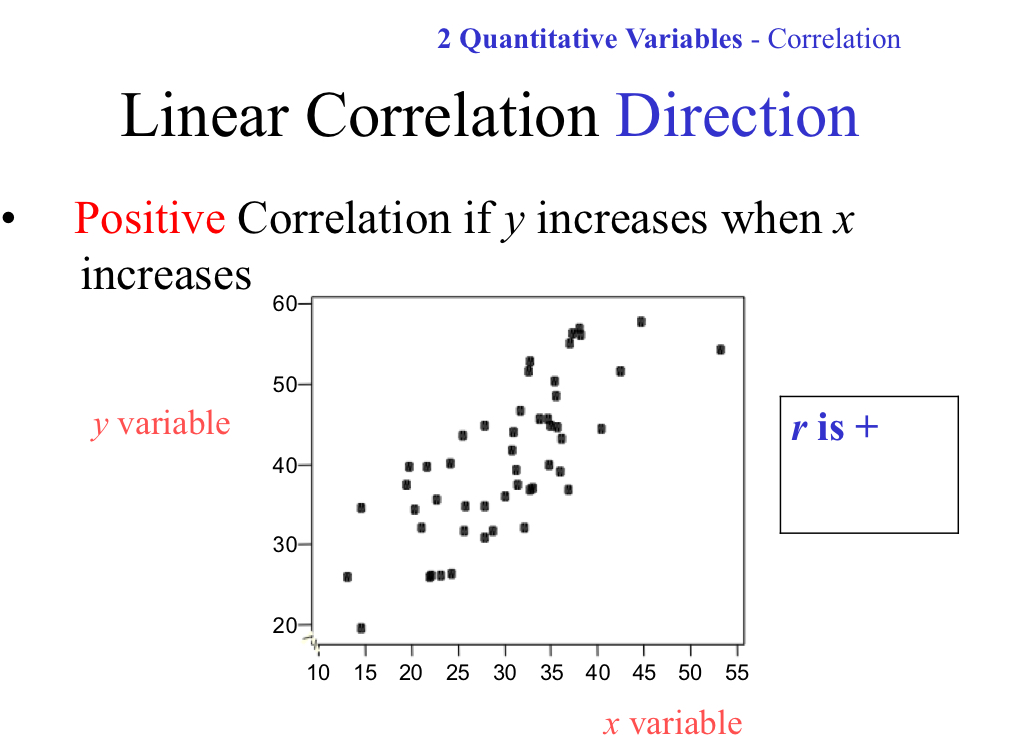
Linear Correlation Direction: Positive Correlation

• When y variable increases, the x variable also increases

• r is a positive value that is greater than 0 and less than 1

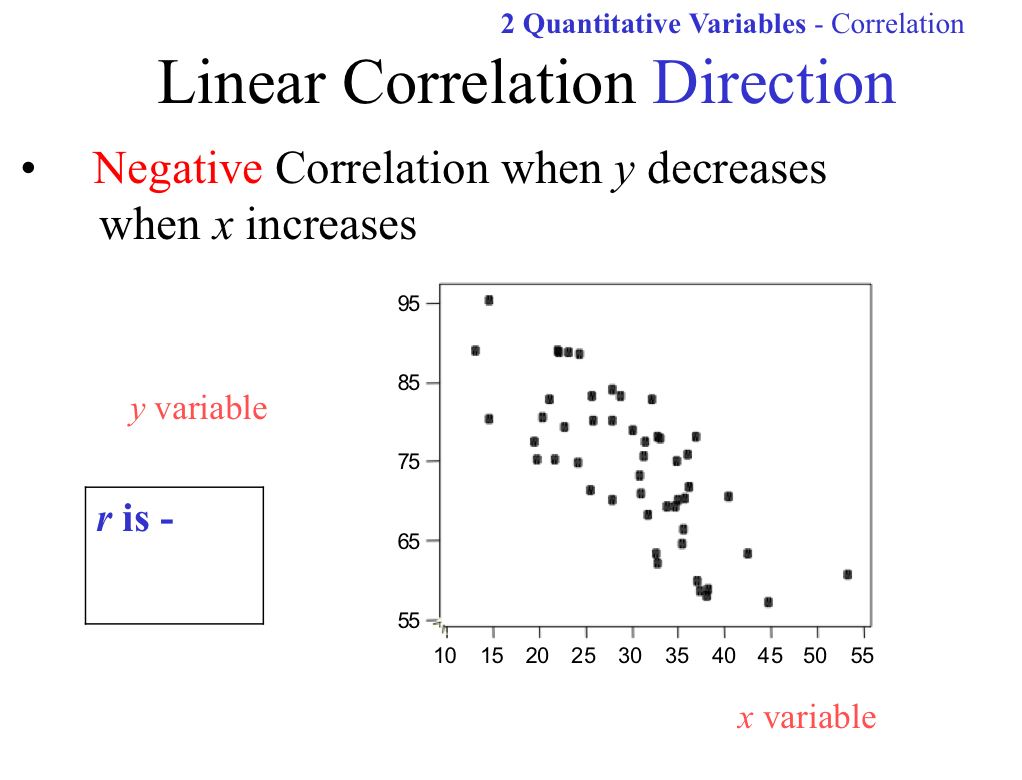
Linear Correlation Direction: Negative Correlation

• When the y variable decreases, the x variable increases

• r is a negative value that is greater than -1 and less than 0

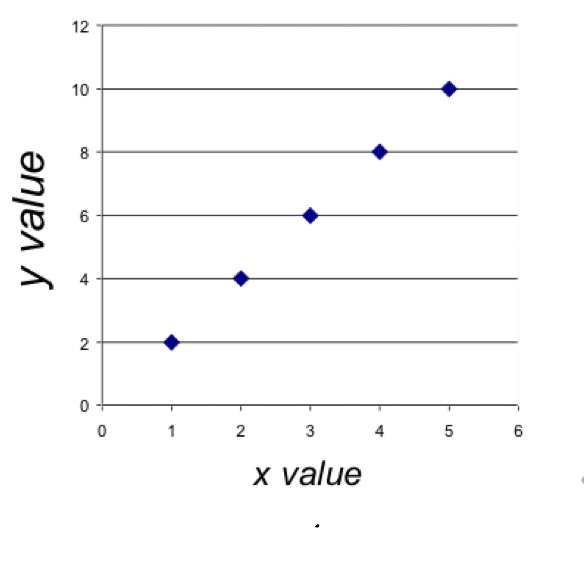
Linear Correlation Strength : r= +1

• Perfect positive correlation

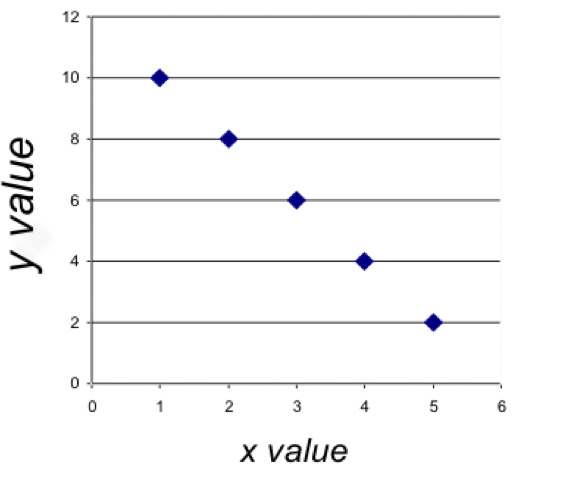
Linear Correlation Strength: r= -1

• Perfect negative correlation

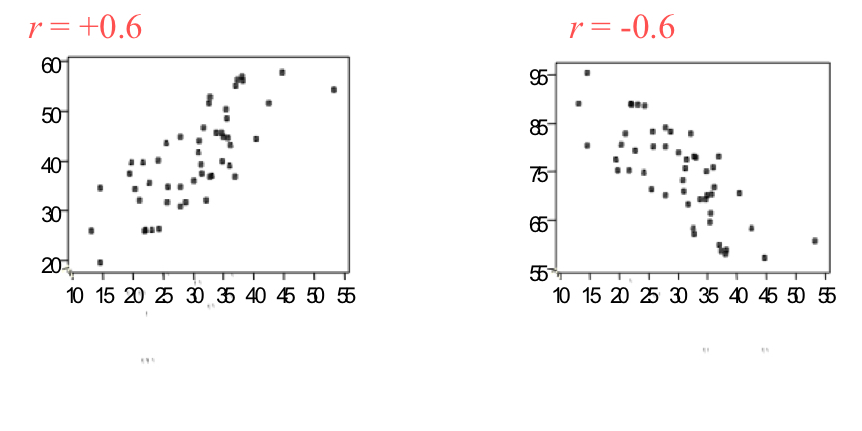
Linear Correlation Strength: r value between -1 and 0 and +1

• Intermediate Relationship

• Typically values from -0.3 and 0 and +0.3 represents a weak or nonexistent relationship between the variables

Example correlation problem : Researchers at Johns Hopkins recently discovered a correlation between dietary fiber in the diet and colon health. People on a high fiber diet have a lower risk of cancer. Is this a negative or positive correlation?

• Negative

  • The x value is increasing while the y value is decreasing

How can r=0 occur? (3 ways)

A) no trend in data (scattered data plots)

B) as the x variable changes and y stays the same (horizontal line) or the y variable changes and the x stays the same (vertical line)

C) There is a relationship but it is not linear (ex: pyramid line)

• A relationship can be missed if it is nonlinear so it should not be analyzed using correlation

Correlation Concerns: Part One

A) Check for nonlinear relationships

• If there is a nonlinear pattern, the data may be able to fit a nonlinear model then be analyzed using correlation afterwards

B) Check for Outliers

• Can move r closer to +1 or 0

• Need a justification to remove valid data from a dataset

C) Correlation is not causation

• Most correlations are done on survey data which cannot determine cause and effect

Correlation Problems: Part 2

D) Third Variable Problem

• A factor that is not evaluated but does impact 2 variables that are measured

F) Do not extrapolate beyond data set

• Do not draw conclusions based on information outside of recorded data

Correct Terminology for Correlation

• Correlation explains how X and Y are associated

• Terms related with correlation:

  • Tends to

  • Linked

  • Connected

  • Tied to

  • Associated

Reporting Correlations

Graphs should include:

• Title

• Clearly labeled axes

• No Regression Line

• Statistical Results

Difference between Correlation and Regression

Correlation: asks if 2 variables vary together

Regression: asks if changes in one variable causes or predicts changes in another variable

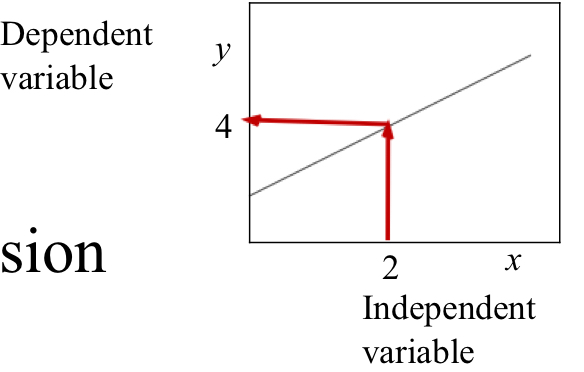
Linear Regression

• Predicts a value for y (output/dependent variable) given an x value (input/independent variable)

  • • Ex: mouse growth (gm) is dependent on amount of food given (gm)

• Minimizes the variability in the y direction and generates the best fit regression line

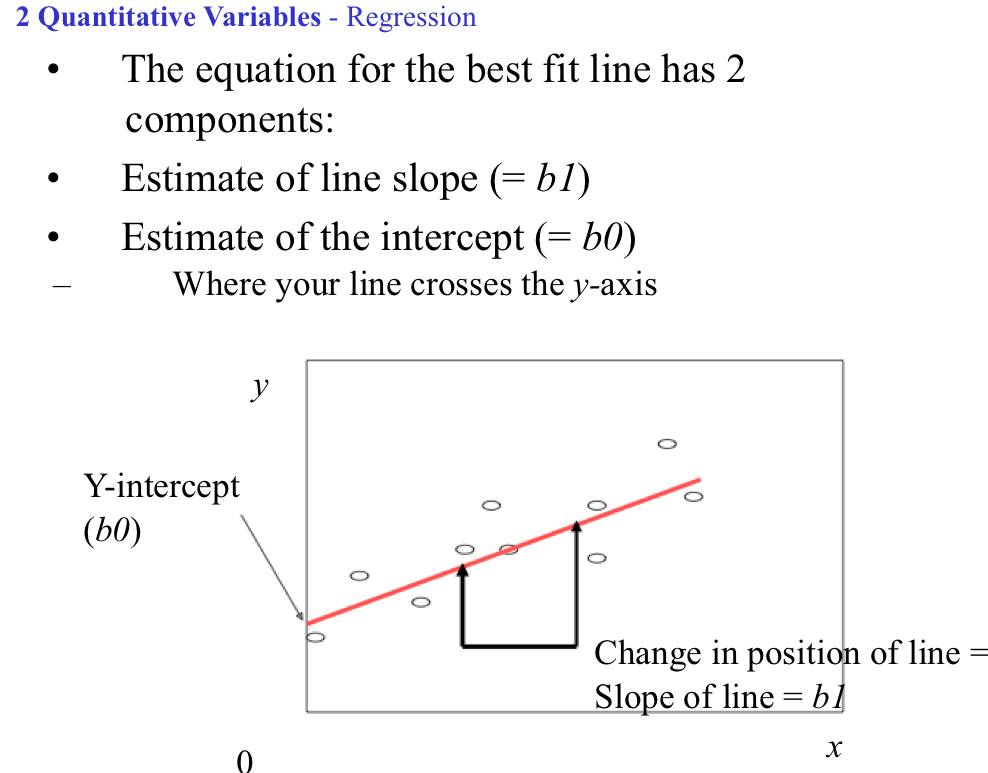
Regression: Best Fit Line

• Determines the Best Fit Line to the data

  • Minimizes deviations between line and actual data points vertically

  • Equation: Y= b0 + b1x

    • Estimate of line slope= b1

    • Estimate of the y intercept= b0

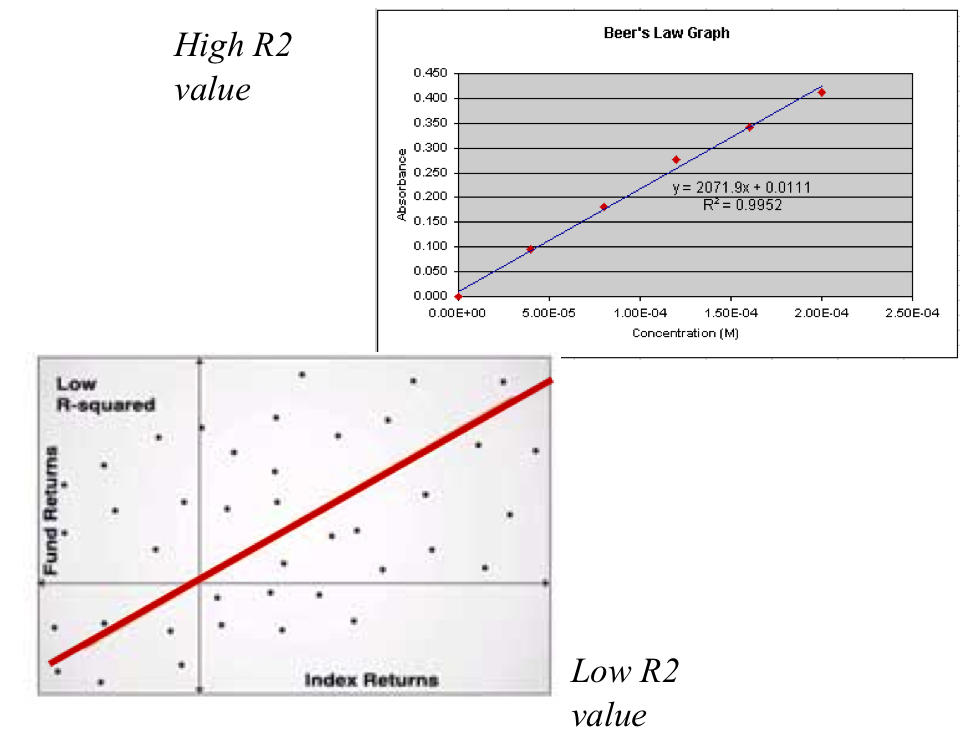
Coefficient of Determination: R2

• Measures the amount of variability in the dependent variable (y) explained by the variability in the independent variable (x)

  • Determines how tight the values are towards the regression line

• Varies from 0 to 1

  • R2=0, no relationship between x and y

  • R2=1, perfect relationship (ex: straight line for linear regression)

R2 vs r.

• r is used for Correlation, gives tightness and direction, values vary from -1 to 0 to +1, can statistically test for relationship between x and y variables

• R2 used for Regression, tells tightness (how close points are to the regression line) only, values vary from 0 to 1, not tested statistically

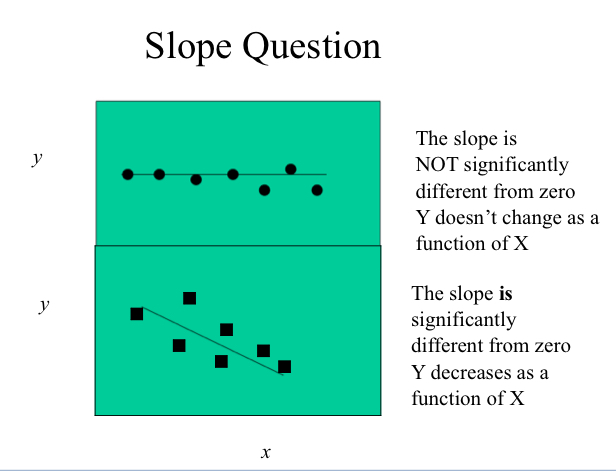
How to test for a relationship for regression?

• Ask if the slope of the line (b1) is statistically significantly different from 0

• Ask if the intercept (b0) is significantly different from zero

  • Regression will start at a number far from zero because of intercept

Components for presenting Regression results

• Title

• Axes labeled units

• Line only in the range of data

• Equation for line

• R2 line

Regression Concerns

• Outliers can have a large impact

• Never extrapolate beyond range of data

• Relationship may be nonlinear, graph data first

• Lurking variables if it is survey data

• Open to different interpretations

Is it correlation or is it regression?

• Correlation looks at the trend of 2 variables while regression asks if the y variable is a function of the x variable

  • For regression, interpretations depend on if a study is a survey or experiement

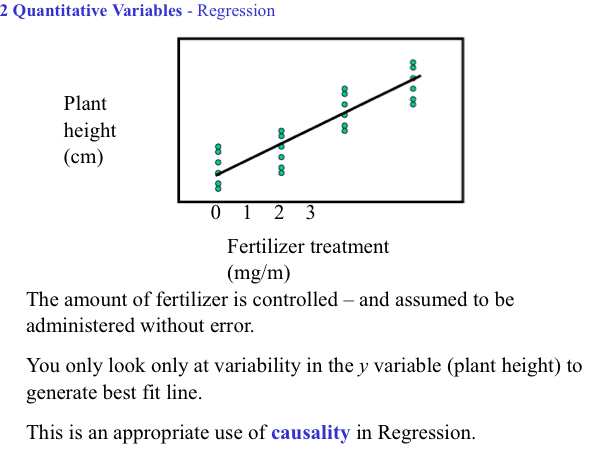
Regression: Causality

• Can only be shown with controlled experiments

  • Ex: experiment with 4 levels of fertilizer (0,1,2, and 3 mg/m). 6 plants assigned to each fertilizer treatment, look at how tall they grow in 2 weeks

Regression vs Correlation

• Correlation can only be used to compare 2 quantitative variables, can only look at the linear relationship typically using survey data

• Regression can include more variables, can deal with curvilinear data, is able to deal with survey and experiment data (causation requires controlled experiment)

  • Can be used for nonlinear relationships