NURS 360- Exam 2- Statistical Analysis of Quantitative Data & Evaluating Clinical Significance

Purposes of Statistical Analysis in Quantitative Research

• To describe the data (e.g., sample characteristics)

• To estimate population values

• To test hypotheses

• To provide evidence regarding measurement properties of quantified variables

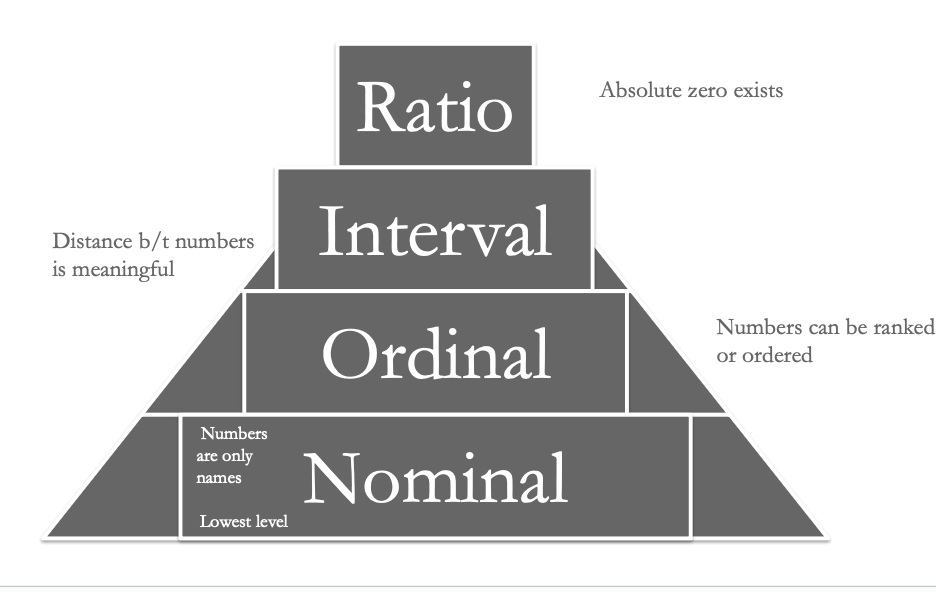
nominal measurement

lowest level; involves using numbers simply to categorize attributes

• Names

  • Lowest level of measurement

  • Data categorized into groups/categories

  • Categories should be mutually exclusive

  • Ex. Male=1 , Female=2, NB=3 

ordinal measurements

ranks people on an attribute

• 2nd lowest level of measurement

• Numeric values on continuum but not equal 

• Ordered and ranked but intervals not equal distance

• Ex: Likert scale

• Ex: Numeric Pain Scale 0-10

  • Differences cannot be specified

interval measurement

ranks people on an attribute and specifies the distance between them

• 3rd level of measurement

• Continuum of numeric values where intervals between numbers are equal but lacks a “true zero”   

  • ex.  Fahrenheit scale 0 does not = no temperature….

• Datum ranked and attributed distance 

• between are equal

• (Equal intervals b/t numbers)

ratio measurements

highest level; ratio scales, unlike interval scales, have a meaningful zero and provide information about the absolute magnitude of the attribute.

• Highest level

• Numeric values assigned to data 

• Begin with zero and have = intervals

• Ex. Age, # hours studied for a test, many biophysiologic--pulse

• Ex.  Amount of money in your bank account

  • 0 balance= NO money

levels of measurement

descriptive statistics

• Used to describe and synthesize data

  • Parameters: descriptor for a population

  • Statistics: descriptive index from a sample

inferential statistics

• Used to make inferences about the population based on sample data

• Assumes random sampling 

frequency distributions

• A systematic arrangement of numeric values on a variable from lowest to highest and a count of the number of times (and/or percentage) each value was obtained

• Can be presented in a table (Ns and percentages) or graphically (e.g., frequency polygons)

• Frequency distributions can be described in terms of:

• Shape

• Central tendency

• Variability

symmetry

symmetric

skewed

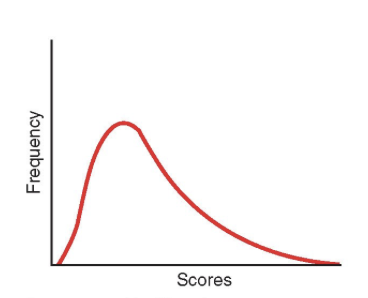
positive skew

long tail points to the right

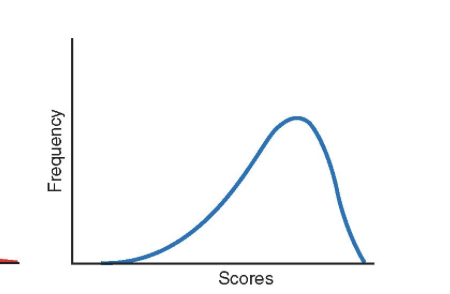
negative skew

long tail points to the left

modality

number of peaks

unimodal

1 peak

bimodal

2 peaks

• normal distribution (a bell-shaped curve)

multimodal

2 + peaks

mode

• the most frequently occurring score in a distribution 

  • Example: 2, 3, 3, 3, 4, 5, 6, 7, 8, 9 Mode = 3

median

• the point in a distribution above which and below which 50% of cases fall

Example: 2, 3, 3, 3, 4 | 5, 6, 7, 8, 9 Median = 4.5

mean

• equals the sum of all scores divided by the total number of scores

Example: 2, 3, 3, 3, 4, 5, 6, 7, 8, 9 Mean = 5.0

mode

number that occurs most frequently in a distribution

median

• useful mainly as descriptor of typical value when distribution is skewed (e.g., household income)

mean

most stable and widely used indicator of central tendency

variability

• The degree to which scores in a distribution are spread out or dispersed

homogeneity

little variability 

heterogeneity

great variability

range

highest value minus lowest value

standard deviation (SD)

average deviation of scores in a distribution

bivariate description statistics

used for describing the relationship btwn two variables

• crosstabs (contingency tables)

• correlation coefficients

correlation coefficients

describes intensity and direction of a relationship

Correlation coefficients can range from:

• −1.00 to +1.00.

negative relationship (0.00 to -1.00)

One variable increases in value as the other decreases, e.g., amount of exercise and weight.

positive relationship (0.00 to +1.00)

Both variables increase, e.g., calorie consumption and weight.

The greater the absolute value of the coefficient,

• the stronger the relationship: 

  • Example: r = −.45 is stronger than r = +.40.

With multiple variables, a _________ can be displayed to show all pairs of correlations.

correlation matrix

Pearson’s r (the product–moment correlation coefficient):

computed with continuous measures

Spearman’s rho:

used for correlations btwn variables measured on an ordinal scale

inferential statics

• Used to make objective decisions about population parameters using sample data

standard error of the mean (SEM)

standard deviation of theoretical distribution

theoretical distribution of means for an infinite number of samples drawn from the sample population 

• Is always normally distributed

• Its mean equals the population mean.

• Its standard deviation is called the standard error of the mean (SEM).

• SEM is estimated from a sample SD and the sample size.

SEM is estimated from:

a sample SD and the sample size

point estimation

a single descriptive statistic that estimates the population value (e.g., a mean, percentage, or OR)

interval estimation

• a range of values within which a population value probably lies

  • Involves computing a confidence interval (CI)

confidence interval (CI)

• reflect how much risk of being wrong researchers take. 

• CIs indicate the upper and lower __________ and the probability that the population value is between those limits.

confidence limits

Hypothesis testing helps researchers to:

make objective decisions about whether results are likely to reflect chance differences or hypothesized effects.

probability

Likelihood or chance that an event will occur in a given situation

how is probability expressed

• ower case p with values expressed as per cents 

  • Ex.   p=0.34 

alpha

• evel of significance = probability of making a Type I error 

  • Threshold at which statistical significance  reached

  • Determined prior to data analysis

α (alpha) =

0.05 unless otherwise stated

decision theory

• Assumes all groups in a study are components of the same population

• To test the assumption of no difference (null hypothesis) a cut-off point is selected prior to analysis

  • Referred to as level of significance or alpha

• Up to researcher to prove there really is a difference

hypothesis testing

• Test research  hypothesis statistically—disprove null hypothesis

• Reject null hypothesis

Significant result 

there is a difference between the two groups not as a result of chance

Non-significant result–

• any difference or relationship could have been purely chance

If the value of the test statistic indicates that the null hypothesis is improbable, then the result is _______

statistically significant.

A ______  means that any observed difference or relationship could have happened by chance.

nonsignificant result

Type I error

• rejection of a null hypothesis when it should not be rejected; a false-positive result

type 1 error

false positive

type 2 error

false negative

type II error

• failure to reject a null hypothesis when it should be rejected; a false-negative result

power

the ability of a test to detect true relationships

larger samples = ____

greater power

not statistically significant

type II errors

findings are statistically significant

type I errors

Analysis of 4 parameters

• Level of significance (alpha)

• Sample size

• Power (beta)

• Effect size

• Tells you how many subjects needed to start and finish the study

bivariate statistical tests

• t-Tests

• Analysis of variance (ANOVA)

• Chi-squared test

• Correlation coefficients

• Effect size indexes

t-test

Tests the difference between two means

t-Test for independent groups:

• between-subjects test

  • For example, means for men vs. women

t-Test for dependent (paired) groups:

within-subjects test

• For example, means for patients before and after surgery

analysis of variance (ANOVA)

• Tests the difference between more than two means

• sorts out the variability of an outcome variable into two components: variability due to the independent variable and variability due to all other sources

Variation between groups is contrasted with variation within groups to yield an F ratio statistic.

• One-way ANOVA (e.g., three groups)

• Multifactor (e.g., two-way) ANOVA

• Repeated measures ANOVA (RM-ANOVA): within subjects
  

chi-squared test

• Tests the difference in proportions in categories within a contingency table

• Compares observed frequencies in each cell with expected frequencies—the frequencies expected if there was no relationship 

correlational coefficient

• Pearson’s r is both a descriptive and an inferential statistic.

• Tests that the relationship between two variables is not zero

Effect size is an important concept in

power analysis.

In a comparison of two group means (i.e., in a t-test situation), the effect size index is

d

Effect size indexes

• summarize the magnitude of the effect of the independent variable on the dependent variable.

d ≤ .20

small effect

d = .50

moderate effect

d ≥ .80

large effect

reliability assessment

• Test–retest reliability

• Interrater reliability

• Internal consistency reliability

validity assessment

• Content validity

• Construct validity

• Criterion validity

hypothesis testing

• The test used

• The value of the calculated statistic

• Degrees of freedom

• Level of statistical significance

A researcher measures the weight of people in a study involving obesity and Type 2 diabetes. What type of measurement is being employed?

ratio

A bell-shaped curve is also called a normal distribution.

true

The researcher subtracts the lowest value of data from the highest value of data to obtain:

range

A correlation coefficient of −.38 is stronger than a correlation coefficient of +.32. 

true

Which test would be used to compare the observed frequencies with expected frequencies within a contingency table?

chi-squared test

six considerations for interpretive task

• The credibility and accuracy of the results

• The precision of the estimate of effects

• The magnitude of effects and importance of results

• The meaning of the results; especially causality

• The generalizability of the results

• The implications of the results for practice, theory, or further research

interpreting research

inferences

inferences

drawing conclusions based on limited information, using logical reasoning.

Evidence-based practice involves

• integrating research evidence into clinical decision making. 

credibility of quantitative results

• Proxies and interpretation

• Credibility and validity

• Credibility and bias

• Credibility and corroboration

CONSORT (The Consolidated Standards of Reporting Trials)

include a flowchart for documenting participant flow in a study

credibility and validity

• Linked with inference

• Statistical conclusion validity

• Internal validity

• External validity

• Construct validity

researcher’s job r/t credibility and bias

• Translate abstracts into appropriate proxies

• Eliminate, reduce, or control biases

• Look out for biases and factor them into assessment about the credibility of the results

seeking evidence to disconfirm the null hypothesis

• Determining quality of the proxies that stand in for abstractions

• Ruling out biases 

• Seeking corroboration for the results

results that support the researcher’s hypotheses are described as:

significant

A careful analysis of study results involves:

evaluating whether, in addition to being statistically significant, the effects are large and clinically important.

An interpretation of meaning requires understanding of:

methodological, theoretical, and substantive issues

Interpreting statistical results is easiest when:

hypotheses are supported, i.e., when there are positive results