Algebraic Proofs and Properties of Equality: Two-Column Proofs and Examples

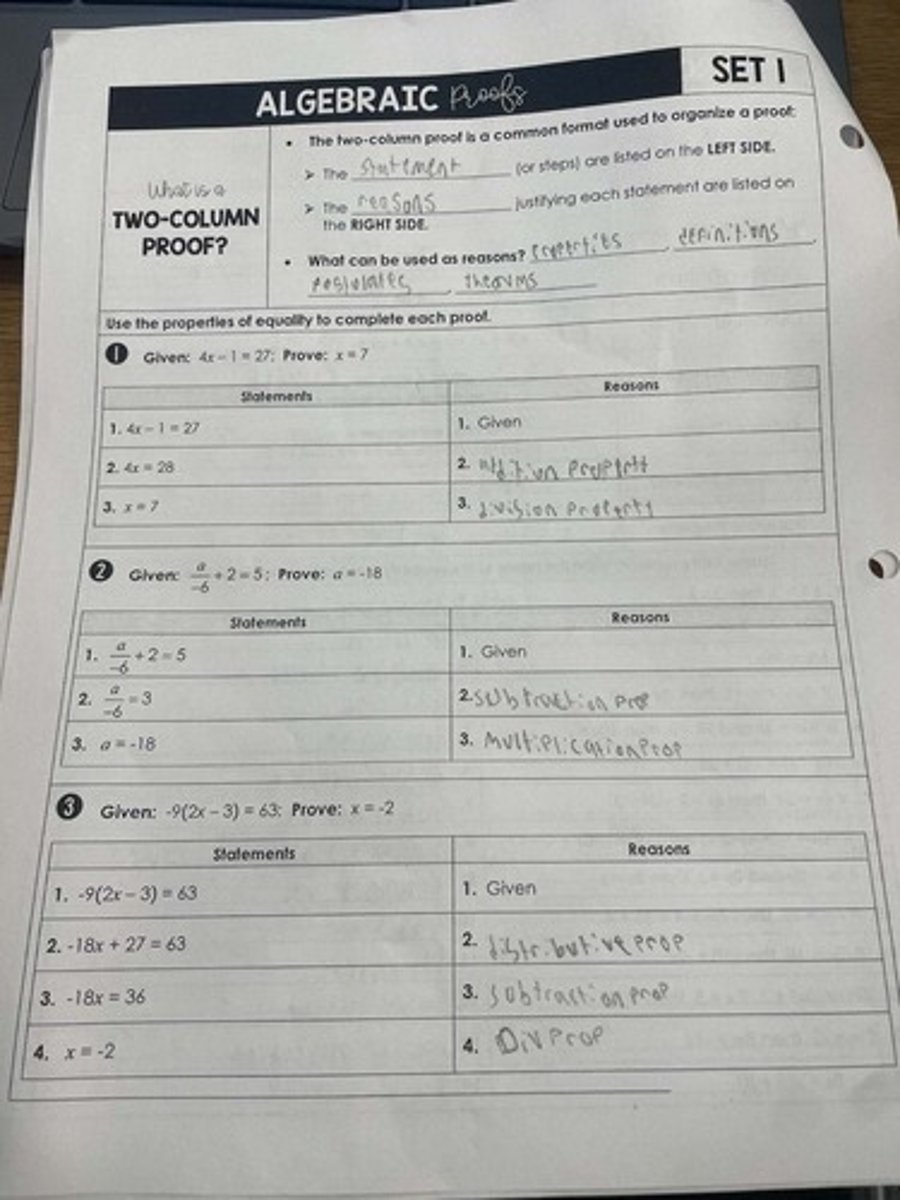
TWO-COLUMN PROOF

The Statement and the reasons justifying each statement are listed on the LEFT SIDE and the RIGHT SIDE.

Addition Property

If a = b, then a + c = b + c.

Subtraction Property

If a = b, then a - c = b - c.

Multiplication Property

If a = b, then a c = b c.

Division Property

If a = b and c ≠ 0, then a / c = b / c.

Distributive Property

a(b + c) = ab + ac.

Substitution Property

If a = b, then a may be replaced by b in any expression or equation.

Reflexive Property

For any real number a, a = a.

Symmetric Property

If a = b, then b = a.

Transitive Property

If a = b and b = c, then a = c.

Given: 4x-1 = 27; Prove: x = 7

1. 4x-1=27; 2. 4x=28; 3. x = 7.

Given: +2=5; Prove: a = -18

1. +2=5; 2. a + 2 = 5; 3. a = -18.

Given: -9(2x-3)= 63; Prove: x = -2

1. -9(2x-3)= 63; 2. -18x+27= 63; 3. -18x=36; 4. x = -2.

Given: 6x+7=8x-17; Prove: x = 12

1. 6x+7=8x-17; 2. 7=2x-17; 3. 24 = 2x; 4. 12 = x; 5. x = 12.

Given: -7(x+2)+4x=6(2x-4); Prove: x = 2/3

1. -7(x+2)+4x=6(2x-4); 2. -7x-14+4x=12x-24; 3. -3x-14=12x-24; 4. -15x-14=-24; 5. -15x=-10; 6. x = 2/3.

Given: 3x + 1 = -14; Prove: x = -5

1. 3x + 1 = -14; 2. 3x = -15; 3. x = -5.

Given: 2(x-9) = -10; Prove: x = 4

1. 2(x-9) = -10; 2. 2x - 18 = -10; 3. 2x = 8; 4. x = 4.

Given: 10k-4 = 2k-20; Prove: k = -2

1. 10k - 4 = 2k - 20; 2. 10k + 16 = 2k; 3. 8k = 16; 4. k = -2.

Given: -8(w + 1) = -5(w+ 10); Prove: w = 14

1. -8(w + 1) = -5(w + 10); 2. -8w - 8 = -5w - 50; 3. -3w = -42; 4. w = 14.

Given: 14-2(x+8)= 5x - (3x-34); Prove: x = -9

1. 14-2(x+8)=5x-(3x-34); 2. 14-2x-16=5x-3x+34; 3. -2x-2=2x+34; 4. -2x=2x+36; 5. -4x=36; 6. x = -9.