Week 3 Lecture 1 - Equivalence of Regular Languages. DFA Minimization

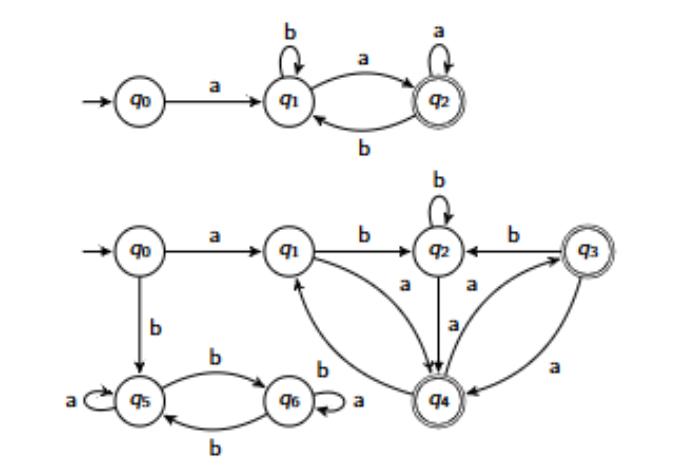
What is the language that both of these FSAs accept?

They both accept strings of length 2 or more that start and end in ‘a’

When is a problem effectively soluble?

If there is an algorithm that always provides the answer in a finite number of steps, not matter what the inputs are.

What is a decision procedure?

An effective solution to a problem that has a yes or no answer.

What is a decidable?

A problem that has a decision procedure.

How do we test whether languages are equivalent?

1. Creating the difference automaton, which accepts strings that are either in 1 of the languages but not the other.

2. Testing whether this automaton accepts any strings.

If the difference automaton accepts no strings, then the languages are equivalent.

Use L₁ and L₂ to transform the equivalence problem. What is the difference FSA?

(L₁ - L₂) U (L₂ - L₁) is the difference automaton.

This is the language consisting of all strings that are in L₁ but not L₂ and all strings that are in L₂ but not in L₁

What is the equivalence for testing emptiness of an FSA?

Equivalent to showing whether there is a path from the start state to an accepting state.

If the accepting states are all seperated from the start state then the language is empty.

Define the recursive process for testing for emptiness of an FSA?

Basis → The start state is surely reachable from the start state.

Induction → If state q is reachable from the start state and there is an arc from q to p with any label (an input symbol or λ) then p is reachable.

In this way, we can compute the set of reachable states. If any accepting state is among them, then we answer no, otherwise yes.

What is the maximum number of steps that the reachability calculation takes when the automaton has n states?

n²

What is the procedure for checking equivalences?

Let F be an FSA with n states.

Prove that if F accepts any input string ‘w’ such that |w| >= n, then F accepts an infinite language.

→ The path taken through F while accepting w goes over at least |w| edges, and hence visit at least |w|+1 states.
→ As there are only n < |w| + 1 states in the automaton, this means at least 2 state must have been visited twice.
→ This implies there is at least 1 loop somewhere along the path taken in accepting |w|.
→ There must therefore be an infinite number of other strings accepted by F, corresponding to taking the same path through F but going round this loop 2 times, 3 times, 4 times….

Let F be an FSA with n states.

Prove that if F accepts infinitely many states, then F accepts some strings ‘w’ such that n =< |w| < 2n

→ If F accepts an infinite language then F contains at least 1 loop.
→ Choose a path with just 1 loop.
→ The length of this loop cannot be greater than n.
→ Then one can construct a path with length at least n+1 but less than 2n+1 by going round the circuit the required number of times.

What is the procedure for checking infiniteness?

1. Generate all strings of length at least n+1 and no more than 2n

2. Check if any is accepted by the FSA.

3. If it is, then the FSA accepts an infinite language; if not it does not.

How do we reduce the number of states in a DFA?

Considering which groups of states are equivalent.

All states are either distinguishable or equivalent.

When are 2 DFA states equivalent?

When are 2 DFA states distinguishable?

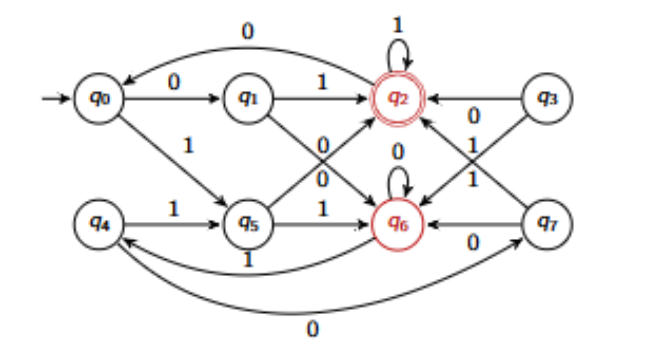
In this DFA, explain why q₂ and q₆ are distinguishable.

λ distinguishes them, meaning they are distinguishable from the start, before any input is processed. This is because q₂ is an accepting state and q₆ isn’t. Therefore, they are different before any input is consumed.

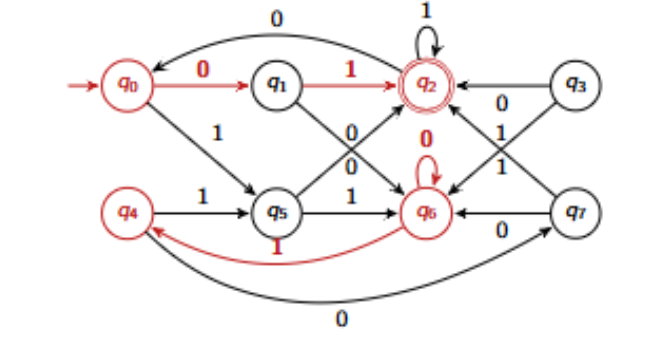
Why are q₀ and q₆ distinguishable in this DFA?

λ does not distinguish them.
0 does not distinguish them.
1 does not distinguish them.
01 does distinguish them because q₂ is accepting and q₄ is not.

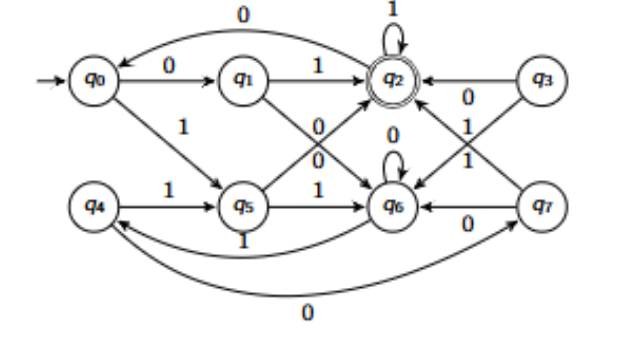
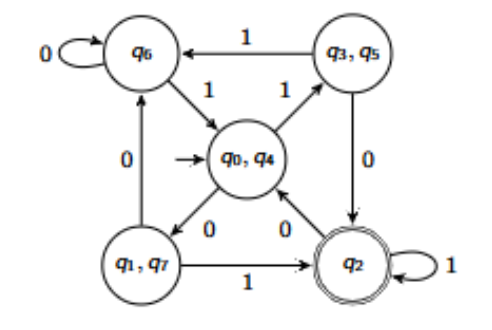
Why are q₀ and q₄ equivalent in this DFA?

They both transition the exact same way no matter the inputs. They will always lead to the same acceptance or rejection no matter what input is consumed. This makes them equivalent.

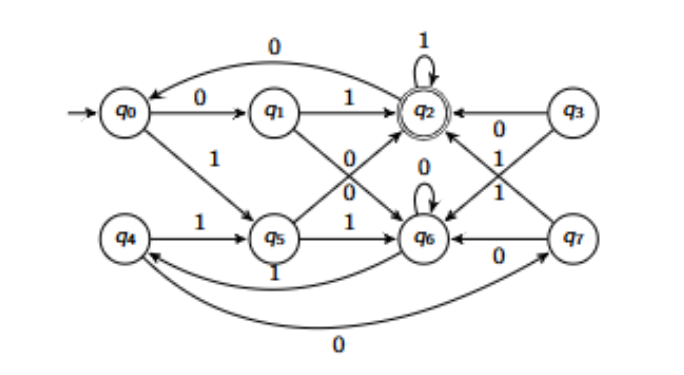
What is the minimised DFA for this example?